Определение внутренних усилий методом сечений. Напряжения
Метод сечений заключается в том, что тело мысленно рассекается плоскостью на две части, любая из которых отбрасывается, и взамен нее к сечению оставшейся части прикладываются внутренние силы, действовавшие до разреза; оставленная часть рассматривается как самостоятельное тело, находящееся в равновесии под действием внешних и приложенных к сечению внутренних сил.
Метод сечений основан на третьем законе Ньютона.
| Оставлен ная часть |
| Отброшен ная часть |
| F2 |
| F1 |
| F1 |
| F2 |
| m1 |
| m1 |
| a a |
| y a a |
| m2 |
| F4 |
| F3 |
| Q |
| a Fr |
| N |
| Mb |
| z |
| M¢b |
| F¢r |
| a a |
| F4 |
| m2 |
| Q |
| F3 |
Рис. 1.1.
Применяя к оставленной части тела условия равновесия, мы сможем найти равнодействующие этих сил.
Основным расчетным объектом в сопротивлении материалов является брус. Рассмотрим, каковы будут статические равнодействующие внутренних сил в поперечном сечении бруса. Рассечем брус (рис. 1.1) поперечным сечением а-а и рассмотрим равновесие его левой части.
Если внешние силы, действующие на брус, лежат в одной плоскости, то в общем случае статическими равнодействующими внутренних сил, действующих в сечении а-а, будут главный вектор Fгл, приложенный в центре тяжести сечения, и главный момент 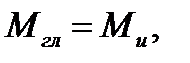 уравновешивающие плоскую систему внешних сил, приложенных к оставленной части бруса.
уравновешивающие плоскую систему внешних сил, приложенных к оставленной части бруса.
Разложим главный вектор на составляющую N, направленную вдоль оси бруса, и составляющуюQ, перпендикулярную этой оси, т. е. лежащую в плоскости поперечного сечения.
Эти составляющие главного вектора вместе с главным моментом назовем внутренними силовыми факторами, действующими в сечении бруса. Составляющую N назовем продольной силой, составляющую Q - поперечной силой, пару сил с моментом 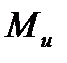 - изгибающим моментом.
- изгибающим моментом.
Для определения указанных трех внутренних силовых факторов статика дает три уравнения равновесия оставленной части бруса, а именно:
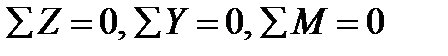
(ось z всегда направляем по оси бруса).
Если внешние силы, действующие на брус, не лежат в одной плоскости, т. е. представляют собой пространственную систему сил, то в общем случае в поперечном сечении бруса возникают шесть внутренних силовых факторов (рис. 1.2), для определения которых статика дает шесть уравнений равновесия:
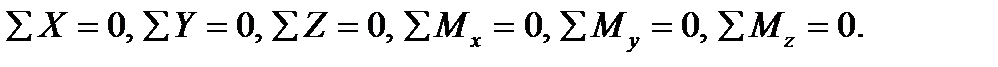
| Mby |
| Mt |
| x |
| N |
| z |
| Mbx |
| Qx |
| Qy |
| y |
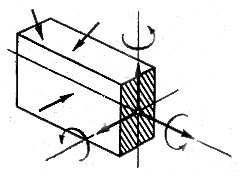
Рис. 1.2.
Шесть внутренних силовых факторов, возникающих в поперечном сечении бруса в самом общем случае, носят следующие названия: N - продольная сила; 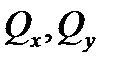 - поперечные силы;
- поперечные силы; 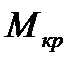 - крутящий момент,
- крутящий момент, 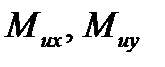 изгибающие моменты.
изгибающие моменты.
При разных деформациях в поперечном сечении бруса возникают различные внутренние силовые факторы. Рассмотрим частные случаи.
1. В сечении возникает только продольная cилa N, в этом случае это деформация растяжения (если сила направлена от сечения) или деформация сжатия (если сила N направлена к сечению).
2. В сечении возникает только поперечная сила Q, в этом случае это деформация сдвига.
3. В сечении возникает только крутящий момент 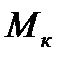 , в этом случае это деформация кручения.
, в этом случае это деформация кручения.
4. В сечении возникает только изгибающий момент 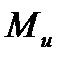 , в этом случае это деформация чистого изгиба. Если в сечении одновременно возникает изгибающий момент
, в этом случае это деформация чистого изгиба. Если в сечении одновременно возникает изгибающий момент 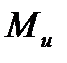 и поперечная сила Q, то изгиб называют поперечным.
и поперечная сила Q, то изгиб называют поперечным.
5. Если в сечении одновременно возникает несколько внутренних силовых факторов (например, изгибающий и крутящий моменты или изгибающий момент и продольная сила), то в этих случаях имеет место сочетание основных деформаций (сложное сопротивление).
Одним из основных понятий в сопротивлении материалов является напряжение. Напряжение характеризует интенсивность внутренних сил, действующих в сечении, т.е. нагрузку, приходящуюся на единицу площади.
Рассмотрим какой-либо произвольно нагруженный брус и применим к нему метод сечений (рис. 1.3).
Выделим в сечении бесконечно малый элемент площади 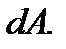 Ввиду малости этого элемента можно считать, что в его пределах внутренние силы, приложенные в различных точках, одинаковы по модулю и направлению и, следовательно, представляют собой систему параллельных сил. Равнодействующую этой системы обозначим
Ввиду малости этого элемента можно считать, что в его пределах внутренние силы, приложенные в различных точках, одинаковы по модулю и направлению и, следовательно, представляют собой систему параллельных сил. Равнодействующую этой системы обозначим 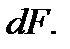 Разделив dF на площадь элементарной площадки dA, определим интенсивность внутренних сил, т. е. напряжение
Разделив dF на площадь элементарной площадки dA, определим интенсивность внутренних сил, т. е. напряжение 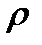 вточках элементарной площадки dA,
вточках элементарной площадки dA, 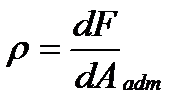 .
.
Таким образом, напряжение естьвнутренняя сила,отнесенная к единице площади сечения. Напряжение есть величина векторная.
Единица напряжения:
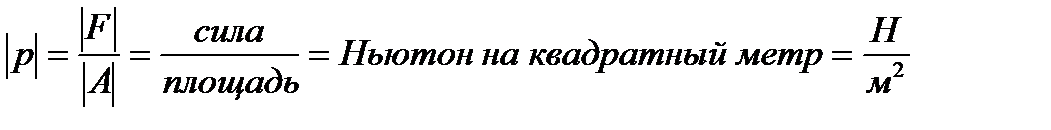 = Паскаль (Па).
= Паскаль (Па).
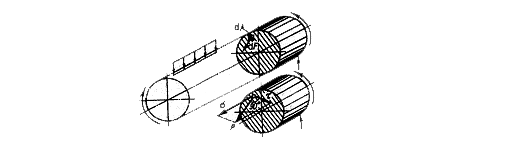
Pис. 1.3.
Поскольку эта единица напряжения очень мала, то мы будем применять более крупную кратную единицу, а именно мегапаскаль (МПа):
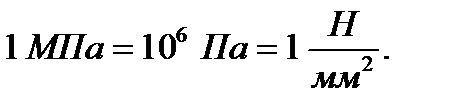
Разложим вектор напряжения 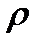 на две составляющие:
на две составляющие:  - перпендикулярную плоскости сечения и
- перпендикулярную плоскости сечения и 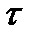 - лежащую в плоскости сечения (см. рис. 1.3). Эти составляющие назовем так:
- лежащую в плоскости сечения (см. рис. 1.3). Эти составляющие назовем так:  - нормальное напряжение,
- нормальное напряжение, 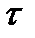 - касательное напряжение.
- касательное напряжение.
Так как угол между нормальным и касательным напряжениями всегда равен 90°, то модуль полного напряжения 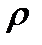 определится по формуле:
определится по формуле: 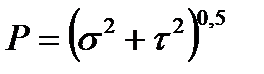 .
.
Дата добавления: 2020-10-25; просмотров: 514;











