Выборочное наблюдение

Суть выборочного наблюдения заключается в том, что из генеральной совокупности (количества единиц N) случайно отбирается n единиц, составляющих выборочную совокупность. Для отобранных единиц рассчитываются обобщенные характеристики (средние или относительные показатели), а затем результаты выборочного обследования распространяются на всю генеральную совокупность.

Проведение статистического наблюдения на выборочной основе позволяет решать задачи:

- обеспечение значительной экономии затрат труда, времени, материальных и финансовых ресурсов при сборе первичных данных;

- уменьшение информационной нагрузки на респондентов;

- сокращение количества ошибок регистрации;

- привлечение к работе персонала более высокой квалификации ;

- получение данных по объектам, по которым сплошное наблюдение невозможно (например, невозможно провести лабораторный анализ качества всей массы полезных ископаемых в разведанном месторождении).

Виды выборочного наблюдения могут быть классифицированы по ряду признаков:

- по единицам отбора - (единица наблюдения и серия (гнездо));

- по повторности отбора - (бесповторная и повторная);

- по способу отбора единиц - (собственно случайный и систематический);

- по типам (стратам) - (стратифицированная и нестратифицированная) ;

- по числу ступеней – (одноступенчатая и многоступенчатая);

- по фазам выборки – (однофазная и многофазная);

- по взаимопроникновению – без взаимопроникновения и взаимопроникающая).

Основной задачей при выборочном наблюдении является определение ошибок выборки, то есть возможных расхождений между выборочной средней и генеральной средней. Различают среднюю и предельную ошибки выборки. Средняя ошибка выборки (μ) характеризует среднюю величину расхождения между выборочной и генеральной средней и представляет собой по форме и содержанию среднее квадратическое отклонение возможных значений выборочной средней от генеральной.

В математической статистике доказано, что средняя ошибка выборочной средней приповторном отборе определяется по формуле:

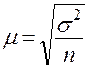, где

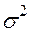- дисперсия изучаемого показателя в генеральной совокупности;

n- объем (численность) выборки.

При бесповторном отборе формула приобретает вид:

,

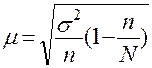где N – численность генеральной совокупности.

Следовательно, средняя ошибка выборки зависит от дисперсии изучаемого признака (прямо пропорциональна, чем больше вариация, тем больше ошибка) и объема выборки (чем она меньше абсолютно и относительно (по доле в генеральной совокупности), тем больше ошибка.

Отклонение выборочной характеристики от генеральной называется предельной ошибкой выборки.

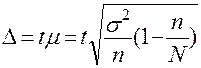- (для бесповторного отбора);

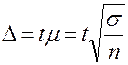- (при повторном отборе),

где - предельная ошибка выборки;

μ - средняя ошибка выборки;

t - коэффициент доверия, то есть показатель, зависящий от вероятности (P), с которой предельная ошибка определяется.

Согласно закону нормального распределения вероятность P может быть найдена как функция от t с помощью интеграла Лапласа,значения которого приводятся в учебниках [1,12,16]. Так, при t = 1 вероятность P = 0,683. Это означает, что с вероятностью 0,683 (или 68,3%) можно гарантировать, что отклонение генеральной средней от выборочной не превысит однократной средней ошибки μ, то есть что в генеральной совокупности среднее значение признака (x_г ) будет находиться в пределах 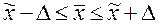, то есть .

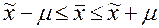При t = 2 вероятность P =0, 954. Это означает, что с вероятностью 0,954 (или с ошибкой менее 5 %) можно гарантировать, что отклонение генеральной средней (x_г) от выборочной (x_в) не превысит двукратной средней ошибки 2μ, то есть что в генеральной совокупности среднее значение признака (x_г ) будет находиться в пределах .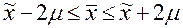

При t = 3 вероятность P =0, 998. Это означает, что с вероятностью 0,998 (или ошибкой менее 1 %) можно гарантировать, что отклонение генеральной средней от выборочной не превысит трехкратной средней ошибки μ, то есть что в генеральной совокупности среднее значение признака (x_г ) будет находиться в пределах .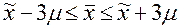

Наряду с абсолютной величиной предельной ошибки в статистической практике рассчитывается относительная ошибка - процентное отношение абсолютной ошибки к исследуемому показателю (средней величине ): .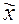

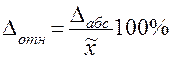Выборка считается репрезентативной, если относительная предельная ошибка не превышает 5 %.

Если n < 20, то выборка считаетсямалой, и при определении предельной ошибки необходимо учитывать два момента. Во-первых, в формуле средней ошибки в знаменателе принимается не n, а n-1. Во-вторых, при нахождении вероятности допуска той или иной ошибки и определении доверительных интервалов исследуемого показателя в генеральной совокупности пользуются таблицами вероятности Стьюдента, приводимыми в учебниках [1, 16 и др.], где P = S (t,n) определяется в зависимости от объема выборки n и коэффициента доверия t.

Формулы предельной ошибки позволяют решить три задачи:

1. Определить доверительные пределы для генеральной средней (или другого показателя, например, доли w):

;

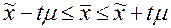или .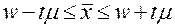

2. Определить вероятность P допуска той или иной заданной предельной ошибки 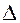. В этом случае определяется t как отношение предельной ошибки 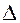к средней ошибке μ и по таблицам вероятностей ( в зависимости от t и n) находится вероятность P.

3. Определить необходимую численность выборки (n), обеспечивающую заданную точность с определенной вероятностью. Формула для n определяется из соответствующих формул для предельной ошибки. Например, для определения средней 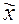из формулы предельной ошибки имеем:

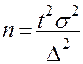- при повторном отборе;

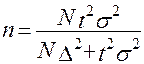- при бесповторном отборе.

Рассмотрим решение задач с применением предельной ошибки выборки.

Задача 1.

Методом собственно случайной выборки обследована жирность молока у 100 коров. По данным выборки средняя жирность оказалась равной 3,64 %, а дисперсия составила 2,56. Определить: а) среднюю ошибку выборки; б) с вероятностью, равной 0.9545, предельные значения генеральной средней.

Решение.

А. По условию n =100, 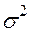= 2,56 и формуле 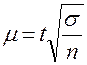получим:

μ = 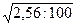= 1,6:10 = 0,16 %.

Б. По приложению 2 в [16] для значения вероятности P =0.9545 находим, что t равно 2. Отсюда t μ = 2 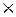0,16 = 0, 32 или

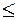
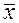
3,64 - 0.32 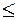3,64 + 0.32.

Следовательно, предельные значения жирности молока (или доверительный интервал генеральной средней) находятся в пределах от 3.32 % до 3,96 %.

Задача 2.

Сколько рабочих завода нужно обследовать в порядке случайной выборки для определения средней заработной платы, чтобы с вероятностью, равной 0.954, можно было гарантировать ошибку не более 50 руб.? Предполагаемое среднее квадратическое отклонение заработной платы σ = 200 руб.

Решение.

Для Р= 0,954, t = 2.

Рассчитаем n по формуле 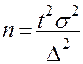=2² 200² : 50²=64 человека.

Следовательно, нужно обследовать в порядке случайной выборки для определения средней заработной платы всех рабочих завода всего 64 человека, чтобы с вероятностью, равной 0.954, можно было гарантировать ошибку не более 50 руб.

КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ

1.В чем состоит роль статистического наблюдения в комплексном экономико-статистическом исследовании?

2. В чем состоят задачи статистического наблюдения?

3.Какие существуют источники и способы сбора статистических данных?

4.Каковы основные направления реконструкции статистического наблюдения с целью совершенствования информационной базы статистики?

5.Назовите основные программно-методологические вопросы статистического наблюдения.

6.Какие требования предъявляются к материалам статистического наблюдения?

7.Какие задачи призваны решать экономические переписи?

8.Поставьте цель, определите объект, единицу наблюдения, конкретные признаки.Составьте программу специального статистического наблюдения.

9.Какое наблюдение называется выборочным?

10.Назовите задачи выборочного наблюдения?

11.Что характеризует средняя ошибка выборки?

12.Какие задачи решаются при использовании выборочного наблюдения?

13.Что может служить основой формирования выборки: а) предприятий, организаций; б) домохозяйств; в) взрослого населения?

14.Как определяется предельная ошибка выборки?

15.Как определить объем (необходимую численность) выборки?

16.Назовите важнейшие области применения выборочного метода в практике государственной статистики.

17.Перечислите виды выборочного наблюдения.

ТЕСТЫ

1. Укажите методы статистики, применяемые на первой стадии статистического исследования (для сбора первичной информации):

а) сводка и группировка;

б) статистические таблицы и графики;

в) массовое статистическое наблюдение;

г) индексный метод;

д) метод обобщающих статистических показателей.

2. Сущность статистического наблюдения заключается:

а) в статистической обработке цифровых данных;

б) в планомерном научно организованном наблюдении (регистрации массовых данных) за явлениями и процессами общественной жизни;

в) в заполнении статистических формуляров;

г) в опросе общественного мнения.

3. К непрерывному статистическому наблюдению относятся:

a) регистрация рождения (брака, развода);

b) переписи.

4. К специально организованным статистическим наблюдениям относятся:

в) отчётность предприятий (организаций);

Г) переписи.

5. К документированному статистическому наблюдению относятся:

в) регистрация рождения (брака, развода);

г) опрос общественного мнения.

6. В плане статистического наблюдения рассматриваются:

а) последовательность проведения статистического наблюдения;

б) программно-методологические и организационные вопросы.

г) множество единиц (явлений, процессов), обладающих массовостью, однородностью и наличием вариации.

7.Статистическое наблюдение – это

a) массовый научно организованный сбор первичной информации об отдельных единицах изучаемого явления;

б) закономерность, присущая явлению;

в) теория статистики;

г) экономическое описание.

8.Статистическое наблюдение для решения фискальных задач на протя­жении всего XVII в., объектом учета которого были толь­ко тягловые дворы, называлось :

a) «Русская Правда»;

б) писцовые и переписные книги;

в) летопись;