Вероятностные методы анализа отклонений параметров
Сущность методов этой группы заключается в том, что отклонения параметра рассматривается как случайная величина, определяемая законами распределения отклонений Dxj параметров xj. Воспользовавшись результатами разложением в ряд Тейлора (п.1.1) зависимости (1.2) получим
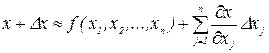 .
.
Найдем математическое ожидание и дисперсию величины x, предполагая для упрощения его симметричное отклонение (номинальное значение xн совпадает с центром поля допуска x0). В этом случае имеем
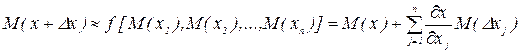
|
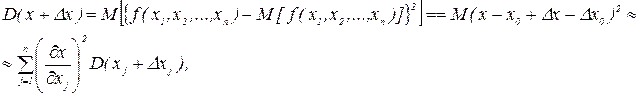
где x0+Dx0=M(x+Dx), x0=M(x) и так как
|
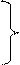 M(x+Dx)=M(x)+M(Dx)
M(x+Dx)=M(x)+M(Dx)
D(x+Dx)=D(x)+D(Dx)
то 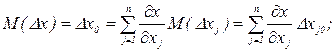
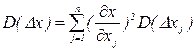 , где Dxj0=M(Dxj).
, где Dxj0=M(Dxj).
Полагая 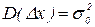 и
и 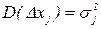 , найдем
, найдем 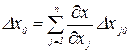 или с учетом формулы (1.5)
или с учетом формулы (1.5)
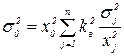 ,
,
где xj0=M(xj).
Для относительных значений, обозначив 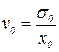 и
и 
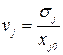 , получим
, получим
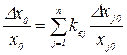 и
и 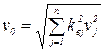 .
.
При использовании приведенных формул следует иметь в виду, что, не смотря на некоторые допущения, сделанные при их выводе (малость величин Dxj и т.д.), они пригодны для определения величин математического ожидания и дисперсии отклонения Dx при любых видах распределения параметров xj и их отклонений Dxj (j=1,2,...,n). Причем при достаточно большой величине n (более 12-15) можно считать, что распределения параметра x и отклонения Dx являются нормальными (или усеченными нормальными) при любых видах распределения параметров xj и их отклонений Dxj.
Основное достоинство методов указанной группы заключается в высокой точности получаемых результатов, учитывающих случайный характер отклонений параметров xj от их номинального значения. Недостатком этих методов является определенная сложность и громоздкость расчетов, особенно в тех случаях, когда распределения параметров xj и (или) их отклонений Dxj отличаются от нормального.
Если отклонения Dxj параметров xj обусловлены влиянием каких-либо внешних воздействий, они не могут считаться независимыми случайными величинами. В этом случае по аналогии с формулами (1.12) и (1.13) можно получить
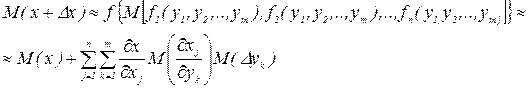
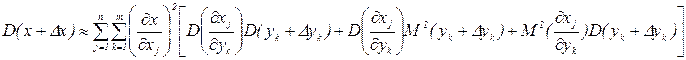
или
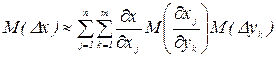 ,
,
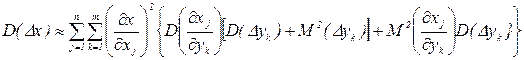 .
.
Ввиду того, что в большинстве практических случаев определение отклонений параметров производится при предельных величинах воздействий yk, можно считать, что 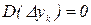 .
.
Полагая 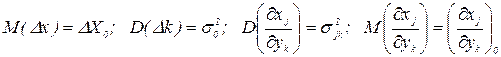 и max(Dyk)=Dyk0, окончательно получим
и max(Dyk)=Dyk0, окончательно получим
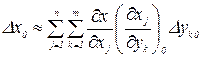 и
и 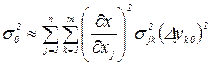 .
.
С учетом формулы (1.5) полученные выражения приводятся к виду
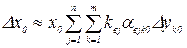 и
и 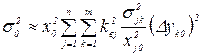 ,
,
где 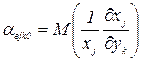 и
и 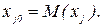
Переходя к относительным значениям и полагая, как и ранее, 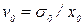 и
и 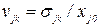 , получим
, получим
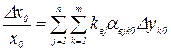 и
и 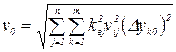 .
.
Приведенные выше формулы для определения величин 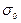 и
и 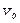 справедливы только в тех случаях, когда отклонения Dхj параметров хj либо являются независимыми случайными величинами, либо обусловлены влияниями внешних воздействий. В случае наличия корреляционных зависимостей величины
справедливы только в тех случаях, когда отклонения Dхj параметров хj либо являются независимыми случайными величинами, либо обусловлены влияниями внешних воздействий. В случае наличия корреляционных зависимостей величины 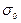 и
и 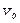 рассчитываются с учетом соответствующих коэффициентов корреляции.
рассчитываются с учетом соответствующих коэффициентов корреляции.
В отдельных случаях, когда используемые в СВТ функциональные элементы содержат сравнительно большое количество компонентов (более 12..15), или несколько функциональных зависимостей 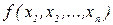 применение приведенных выше методов все же является сравнительно сложным процессом. В подобных случаях коэффициенты влияния наиболее эффективно определять экспериментально.
применение приведенных выше методов все же является сравнительно сложным процессом. В подобных случаях коэффициенты влияния наиболее эффективно определять экспериментально.
Дата добавления: 2020-10-25; просмотров: 509;











