Обработка статистических данных при конструировании и испытаниях СВТ

Получение наиболее достоверного результата измерения и оцен­ка его погрешности - основная цель обработки данных, получен­ных в ходе эксперимента. Выбор метода обработки зависит от чис­ла экспериментальных данных (многократные, однократные изме­рения), вида измерений, вида распределения погрешностей изме­рений, требований к быстроте получения результатов, трудоемкос­ти обработки.

Для оценки результата однократного измерения используют ре­зультаты специально поставленного эксперимента или данные пред­варительных исследований условий измерений, погрешности ис­пользованных средств и методов измерений, субъективных погреш­ностей.

При определении результата многократных измерений обычно используются различные вероятностные методы оценки. Наибольшее распространение нашли статистические методы об­работки (при условии, что распределение полученного ряда эксперимен­тальных данных не противоречит нормальному закону распределения).

В ряде случаев получить весь массив экспериментальных дан­ных сразу невозможно, но их можно получить в разное время, т.е. выполнить измерения в различных условиях. Поэтому в результате получается несколько групп данных, которые требуют совместной обработки.

Немаловажное значение при обработке результатов имеют бы­строта получения результата и трудоемкость метода обработки. Ча­ще всего в качестве результата используют среднее арифметичес­кое значение, а в качестве характеристики его погрешности - сред­нее квадратическое отклонение.

Для того чтобы погрешности вычислений не могли исказить последнюю значащую цифру ре­зультата, при проведении обработки сохраняют необходимое число значащих цифр. Обычно при вычислениях удерживают на одну - две циф­ры больше, чем требуется в окончательном результате.

До начала обработки экспериментальные данные тщательно анализируются. Сначала выявляют отдельные результаты измерений, значения которых резко отличаются от остальных. Этот результат исключа­ют из последующей обработки только в том случае, если имеется твердая уверенность, что допущено неверное действие эксперимен­татора. Во всех других случаях используются статистические ме­тоды определения наличия грубых погрешностей в серии измере­ний.

Существенное значение при выборе метода обработ­ки имеет число измерений, особенно, если обработка выполняется вручную. Большое число измерений усложняет расчеты, создает до­полнительные источники ошибок при вычислениях. Для упрощения расчетов в случаях большого числа измерений принято группиро­вать данные (при n >50), т. е. проводится разделение ряда экспе­риментальных данных от наименьшего х_тin до наибольшего х_тax на k интервалов. Количество интервалов может быть следующее:

Количество измерений п Количество интервалов k

40-100 1-9

100-500 8-12

500-1000 10-16

1000-10000 12-22

Количество интервалов можно подсчитать также по формуле Старджесса

l=1+3,3lgn,

где п - число наблюдений (измерений).

Например, для n=100 получим l=8.

Затем выбирают ширину интервала h, которая должна быть больше ошибок округления при вычислениях 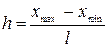. Вычисленное значение ширины интервала округляют. Например, при x_min= 11, х_max = 24, п = 100, h= (24-11 )/8 = 1,63 ≈ 2.

Установив границы интервалов, подсчитывают число резуль­татов измерений n_i, попавших и каждый интервал.

Для предварительной оценки вида распределения по получен­ным данным строят гистограмму распределения, представляющую собой ступенчатую фигуру, состоящую из прямоугольников, основа­ниями которых служат отрезки, изображающие интервалы ряда, а их высоты равны количеству данных n_i, попавших в каждый интервал.

Иногда строят также полигон распределения для изображения дискретного статистического ряда, который представляет собой ло­маную линию, показанную на рисунке 2.1.

Далее проводится проверка гипотезы о том, что распределение данных не противоречит теоретическому распределению, которая проводится по методике, описанной ниже.