Обработка прямых многократных измерений
Рассмотрим, прежде всего, статистические измерения, при которых многократные измерения проводятся для уменьшения влияния случайных погрешностей. Результат каждого измерения xi при этом дает оценку измеряемой величины.
Результат наблюдения xi отличается от истинного xи значения измеряемой величины из-за случайной Δсл и систематической Δст составляющих погрешности
xi = xи+Δсл+Δст .
Повторяя наблюдение, можно получить информацию о случайной погрешности. О систематической погрешности из этих наблюдений информацию извлечь нельзя. Для оценки систематической погрешности необходимо знать свойства используемых средств измерений, метод измерений и условия измерений.
Считается, что для нормального закона распределения среднее арифметическое значение является самой эффективной оценкой измеряемой величины.
В общем случае алгоритм обработки результатов многократных измерений состоит в следующем:
1 Исключают из результатов наблюдений известные систематические погрешности Δст. Если известно, что все результаты наблюдений отягощены одинаковой постоянной систематической погрешностью, ее исключают из результата измерений.
2 Если есть подозрение о наличии анормальных наблюдений (грубых погрешностей, промахов), то проверяют эту гипотезу. Для этого находят предварительные значения среднего арифметического 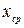 (исключив из него систематическую погрешность Δст) и среднее квадратическое отклонение
(исключив из него систематическую погрешность Δст) и среднее квадратическое отклонение 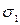 . Затем вычисляют отношение для анормального наблюдения
. Затем вычисляют отношение для анормального наблюдения 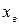
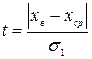
и сравнивают его с табличным значением tГ,, имеющим для данного числа n и уровня значимости q3 определенное значение и выбранное из таблицы П4.2. Если t>tГ , то хв можно считать анормальными и исключить их из дальнейшей обработки (отбросить).
3 Вычисляют среднее арифметическое значениеисправленных результатов наблюдений 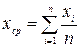 . Если все результаты наблюдений хi отягощены одинаковой погрешностью Δ, то сначала вычисляют среднее арифметическое неисправленных результатов измерений:
. Если все результаты наблюдений хi отягощены одинаковой погрешностью Δ, то сначала вычисляют среднее арифметическое неисправленных результатов измерений: 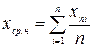 где xнi - неисправленный результат i-го измерения, а затем вычисляют исправленный результат измерений
где xнi - неисправленный результат i-го измерения, а затем вычисляют исправленный результат измерений 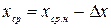 .
.
4 Вычисляют оценку среднего квадратического отклонения результата наблюдений по формуле
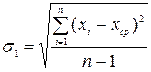 .
.
5 Рассчитывают оценку среднего квадратического отклонения среднего арифметического значения (результата измерений) по формуле
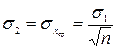 .
.
6 Определяют принадлежность результатов наблюдений нормальному распределению.
7 Определяют доверительные границы 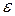 случайной погрешности результата измерений по формуле
случайной погрешности результата измерений по формуле
8 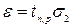 ,
,
где tn,p - коэффициент, определяемый по таблице распределения Стьюдента (П4.3) по заданной доверительной вероятности p (или 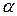 ) и числу наблюдений n.
) и числу наблюдений n.
9 Определяют границы 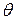 не исключенной систематической погрешности. Если известно, что погрешность результата измерений определяется рядом составляющих не исключенных систематических погрешностей, каждая из которых имеет свои доверительные границы, то при неизвестных законах распределения их границы суммарной погрешности находят по формуле
не исключенной систематической погрешности. Если известно, что погрешность результата измерений определяется рядом составляющих не исключенных систематических погрешностей, каждая из которых имеет свои доверительные границы, то при неизвестных законах распределения их границы суммарной погрешности находят по формуле
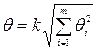 ,
,
где m – число не исключенных систематических составляющих погрешности результата измерения;
k - коэффициент, принимаемый равным 1,1 при доверительной вероятности p= 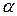 =0,95 и зависящий от числа не исключенных составляющих систематических погрешностей.
=0,95 и зависящий от числа не исключенных составляющих систематических погрешностей.
10 Определяют соотношение 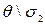 . Если это соотношение меньше 0,8, то не исключенными погрешностями пренебрегают и в качестве границы погрешности результата измерений принимают Δ=
. Если это соотношение меньше 0,8, то не исключенными погрешностями пренебрегают и в качестве границы погрешности результата измерений принимают Δ= 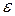 . Если
. Если 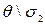 >8, то пренебрегают случайной погрешностью и считают, что Δ=
>8, то пренебрегают случайной погрешностью и считают, что Δ= 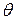 . Если 0,8<
. Если 0,8< 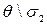 <8, при определении границ погрешности Δ следует учитывать и случайную и систематическую составляющие.
<8, при определении границ погрешности Δ следует учитывать и случайную и систематическую составляющие.
11 Определяют границу погрешности результата измерений по формуле
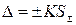 ,
,
где 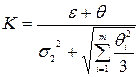 ,
,
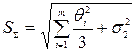 .
.
12 Представляют результат измерения и погрешности для случая симметричных доверительных границ в форме 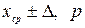 .
.
Дата добавления: 2020-10-25; просмотров: 527;











