Методы математического моделирования

Анализ отклонений параметров конструкции СВТ

Отклонения параметров СВТ от их номинального значения определяют ее устойчивость к дестабилизирующему воздействию различных факторов. При больших величинах этих отклонений существенно ограничивается область рационального применения данного вида СВТ, так как не обеспечивается ее функционирование с требуемыми показателями.

Следует иметь в виду, что знак отклонения параметра в данном случае не имеет значения, так как, например, при уменьшении К_у усилителя не обеспечивается требуемая величина выходной мощности, а при увеличении К_у возможно возникновение самовозбуждения.

Уменьшение влияния дестабилизирующих факторов на отклонение параметров связано с коренным изменением ряда технологических процессов или с применением специальных мер (термостатирования, амортизации, герметизации и пр.), существенно повы­шающих стоимость разработки, изготовления и эксплуатации СВТ.

Одной из основных задач конструирования СВТ является обеспечение возможности ее функцио­нирования в заданных условиях эксплуатации. Очевидно, что решение этой задачи неразрывно связано с определением предельных полей рассея­ния параметров, обуславливающих нормальное функционирова­ние СВТ, и нахождением степени соот­ветствия этих полей установленным допускам.

В настоящее время для определения предель­ных полей рассеяния параметров СВТ применяется ряд методов, основанных на принципах математи­ческого или физического моделирования.

Методы математического моделирования

Сущность этих методов заключается в определении расчет­ным (аналитическим) или статистическим путем связи между отклонениями какого-либо выходного параметра СВТ (или ее части) и причинами, вызывающими эти отклонения. При этом определяется предельное поле рас­сеяния этого параметра при совместном влиянии нескольких факторов (прямая задача) или допустимые отклонения отдельных параметров по заданному до­пуску на выходной параметр (обратная задача).

Решение обратной задачи может быть получено при некоторых до­полнительных условиях, либо связывающих величины отклонений отдельных параметров, либо определяющих оптимальность полученного решения по не­которому критерию, например - стоимости, минимуму типономиналов и т.п.

В основу рассматриваемой группы методов расчета кладутся известные зависимости величины выход­ного параметра от величин параметров элементов (х₁, х₂, ..., х_n), входящих в состав СВТ (или ее части), вида

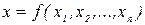. (1.1)

Указанные зависимости являются либо известными, либо могут быть определены экспериментальным или расчетным путем. В случае если величины параметров элементов под влиянием тех или иных воздействий изменятся и станут равными 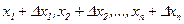очевидно, изменится и величина выход­ного параметра х.

Имеем

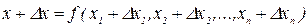(1.2)

и

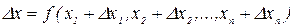
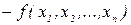. (1.3)

С помощью формулы (1.3) можно решать обе сформули­рованные выше задачи - определение величины Dх по задан­ным величинам 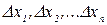и определение величин 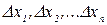по заданной величине Dх. Обычно величины 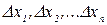невелики, а функции 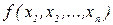до­пускают разложение в ряд Тейлора. С учетом формулы (1.2) можно получить

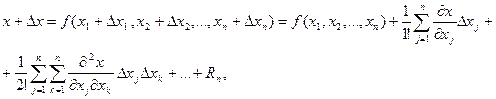
где 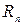- остаточный член разложения 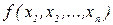в ряд Тейлора.

Учитывая, что согласно сделанному выше замечанию 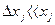(j=1,2,…n) легко найдем, что с достаточной для практики точ­ностью справедлива формула

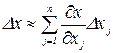, (1.4)

носящая название уравнения погрешностей в абсо­лютных значениях.

На практике допуска отдельных пара­метров обычно задаются не в абсолютных, а в относительных значениях (при условии, что 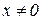и 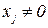). Разделив обе части формулы (1.4) на х, после небольших преобразований получим уравнение погреш­ностей в относительных значениях.

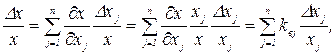(1.5)

где 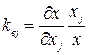- коэффициент влияния 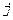-го параметра.

Из формулы (1.5) следует, что

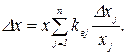(1.6)

Предположим, что изменения параметров х_j являются следствием изменяющихся воздействий у₁, у₂,..,у_m , поэтому

,

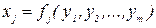и, следовательно,

.

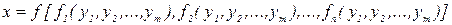Распространяя сделанные выше предположения о свойствах функции 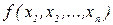на функции 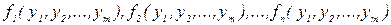, найдем

(1.7)

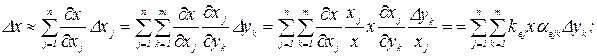
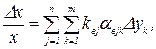
где 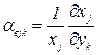- коэффициент неустойчивости параметра х к воздействию .

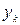С помощью формул (1.5) и (1.6) или (1.7) можно решать обе сформулированные выше задачи.

Коэффициенты неустойчивости 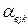определяются как отно­сительные изменения j-го параметра на единицу k-го воздей­ствия и измеряются в величинах, размерность которых обратна размерностям соответствующих воздействий. Зная коэффициен­ты неустойчивости 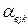, легко определить отклонение соответ­ствующего параметра Dx_j под влиянием воздействий заданной величины Dy_k. Имеем

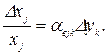
Эта формула широко поменяется при определении отклонений параметров, вызванных температурными полями и явле­нием старения.

Во всех практических случаях сложность современной СВТ весьма велика, число аргументов х_j в формуле (1.1) достигает нескольких тысяч и получение зави­симостей вида (1.5),(1.6) или (1.7) является весьма трудо­емким процессом, не говоря уже о трудностях, связанных с нахождением в аналитическом виде всех частных производных 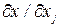и расчетом их величин при заданных условиях эксплуатации.

Для решения задачи о нахождении уравнения погрешностей, СВТ целесообразно расчленить на функциональные элементы (ФЭ) и составить уравнения погрешностей для каждого из них, а также найти общее уравнение погрешностей, учитывающее наличие всех ФЭ.

При­менение рассмотренного приема наиболее эффективно при использовании в СВТ унифицированных ФЭ, так как в этом случае достаточно составить уравнения погрешностей для разных типов применяемых ФЭ и найти величины соответствующих коэффициентов влия­ния.

Все методы математического моделирования можно разделить на две группы: метода анализа по предельным отклонениям параметров, обычно называемые методами максимума-минимума и вероятностные методы анализа.