Законы распределения функций случайных величин. Предельные теоремы теории вероятностей.

Если Х непрерывная случайная величина с плотностью f(x), а случайная величина Y связана с нею функциональной зависимостью

Y=φ(X) где

φ – дифференцируемая функция монотонная на всем участке возможных значений аргумента Х, то плотность случайной величины Y выражается формулой

g(y) = f(ψ(y))| ψ^’(y)|

где ψ – функция обратная по отношению к φ.

Если φ – функция немонотонная, то обратная функция неоднозначна, и плотность случайной величины Y определяется в виде суммы стольких слагаемых, сколько значений (при данном у) имеет обратная функция:

g(y) = 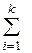f(ψ_i(y))| ψ_i^’(y)|

где ψ₁(у), ψ₂(у), … ψ_к(у) – значения обратной функции для данного у.

Для функций нескольких случайных величин удобнее искать не плотность распределения а функцию распределения. В частности для функции двух аргументов Z=φ(X,Y) функция распределения

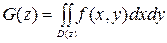, где

f(x,y)- совместная функция плотность величин X и Y; D(z) – область на плоскости xOy, для которой φ(X,Y)<z

Плотность распределения суммы двух случайных величин Z=X+Y выражается любой из двух формул:

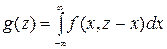
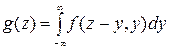
Если случайные величины Х и Y независимы f(x,y)=f₁(x) x f₂(y)

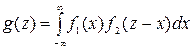
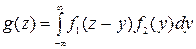
Предельные теоремы теории вероятностей образуют две группы теорем:

1) закон больших чисел и 2) центральная предельная теорема. Закон больших чисел имеет несколько форм, каждая из которых устанавливает ту или иную устойчивость средних при большом числе наблюдений

Пусть имеется последовательность случайных величин Х_1, Х₂, …Х_n,…

Говорят, что эта последовательность сходится по вероятности к неслучайной величине а если при неограниченном увеличении n вероятность события {|X_n-a|<ε} (где ε>0 – произвольно малое фиксированное число) стремится к единице.

1. Теорема Я. Бернулли (простейшая форма закона больших чисел). При неограниченном увеличении числа n независимых опытов, в каждом из которых событие А появляется с вероятностью р, Частота Р*_n события А сходится по вероятности к вероятности р этого события

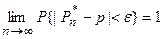
Где ε – сколь угодно малое положительное число.

2. Теорема Пуассона. При неограниченном увеличении числа n независимых опытов, в которых событие А появляется с вероятностями р₁, р₂, …,р_n частота Р*_n события А сходится по вероятности к средней вероятности события:

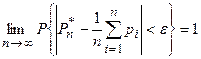
3. Теорема Чебышева (закон больших чисел). При неограниченном увеличении числа n независимых опытов, в каждом из которых случайная величина Х с математическим ожиданием m_х принимает какое-то значение Х_i, среднее арифметическое этих значений сходится по вероятности к математическому ожиданию случайной величины Х:

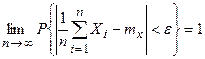
4. Теорема Маркова (закон больших чисел для разных условий опыта). Если

Х_1, Х₂, …Х_n независимые случайные величины с математическими ожиданиями 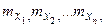и дисперсиями 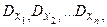причем все дисперсии ограниченны сверху одним и тем же числом L то при неограниченном возрастании n среднее арифметическое наблюденных значений случайных величин сходится по вероятности к среднему арифметическому их математических ожиданий:

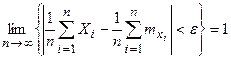
При оценке скорости сходимости по вероятности различных средних к постоянным величинам можно пользоваться неравенством Чебышева:

Р{|X-m_x|≥α}≤D_x/α², где

Α>0; m_x, D_x – математическое ожидание и дисперсия случайной величины Х.

Центральная предельная теорема имеет различные формы. Приведем три.

1. Теорема Лапласа. Если производится n независимых опытов, в каждом из которых событие А имеет вероятность р, то при n 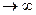закон распределения случайной величины Х – числа появлений события - неограниченно приближается к нормальному закону с параметрами v=np; 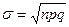(q =1-p)

На основе этого можно вычислить вероятность попадания величины Х на любой участок (α,β) при достаточно большом n

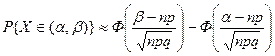
Вместо приведенной формулы часто пользуются выражением для вероятности попадания на участок не самой случайной величины Х а нормированной величины

Z=(X-m_x)/σ_x = (X-np)/ 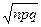; m_z = 0, σ_z = 1

При достаточно больших n

P{Z 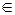(α, β) 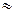Ф(β) – Ф(α)

(

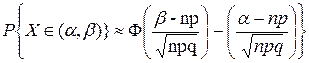
Другая формулировка теоремы Лапласа:

Р(Х<β) = 0,5+Ф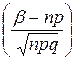

Р(Z<β) = 0,5+Ф(β)

2. Центральная предельная теорема для одинаково распределенных слагаемых . Если Х_1, Х₂, …Х_n одинаково распределенные независимые случайные величины с математическим ожиданием m_x и средним квадратическим отклонением σ_х то их сумма 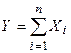при достаточно большом n имеет приближенно нормальное распределение с параметрами

m_y = nm_x, σ_y = 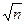σ_x

3. Теорема Ляпунова. Если

Х_1, Х₂, …Х_n независимые случайные величины с математическими ожиданиями 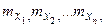и дисперсиями 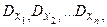причем выполняется ограничение

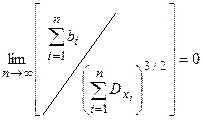
Где b_i = M[|X_i|³], то случайная величина 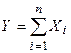при достаточно большом n имеет приближенно нормальное распределение с параметрами

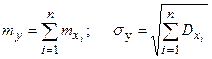
Для доказательства предельной теоремы Ляпунов ввел метод характеристической функции. То есть необходимо рассмотреть комплексные случайные величины. Характеристической функцией с.в.Х называется математическое ожидание комплексной с.в. Y

Θ_x(t) = M[Y] = M[e^itX]

Метод характеристических функций широко применяется для решения вероятностных задач..

Контрольные вопросы:

1.Чему равна плотность случайной величины Y, связанной со случайной величиной Х функциональной зависимостью Y=φ(X), если плотность случайной величины Х равна f(x)?

2. Чему равна функция распределения G(z) функции двух случайных аргументов Z=φ(X,Y) , если совместная плотность распределения равна f(x,y)?

3. Чему равна плотность распределения g(z) суммы двух независимых случайных величин, имеющих плотности распределения f₁(x) и f₂(x)?

4. Сформулировать теорему Бернулли.

5. Сформулировать теорему Пуассона.

6. Сформулировать теорему Чебышева (закон больших чисел).

7. Сформулировать неравенство Чебышева. Найти вероятность того, что случайная величина отходит от своего математического ожидания меньше чем 3σ.

8. Сформулировать теорему Лапласа.

Случайные функции

Функция Х(t) называется случайной , если ее значение при любом аргументе является случайной величиной. Пример случайной функции температура воздуха в данном пункте в данный момент времени в зависимости от высоты.

Понятие случайной функции является обобщением понятия случайной величины. Так как случайную величину Х можно рассматривать как функцию элементарного события ω

Х = φ(ω) (ω 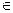Ω), где Ω – пространство элементарных событий, то случайную функцию Х(t) можно представить в виде

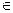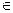X(t) = φ(t,ω) (ω Ω, t T)

Где t не случайный аргумент, Т – область определения функции X(T) .

Реализацией случайной функции X(t) называется конкретный вид , который она принимает в результате опыта (когда осуществилось элементарное событие ω).

Ряд проведенных опытов, исход каждого из которых - случайная функция X(t) дает совокупность реализаций x₁(t), x₂(t), … x_n(t) этой случайной функции. Реализации отличаются друг от друга . Для фиксированного аргумента t случайная функция превращается в обычную случайную величину. Эта случайная величина называется сечением случайной функции.

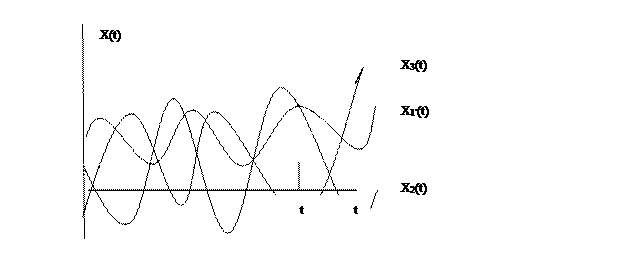
Одномерным законом распределения случайной функции X(t) называется закон распределения сечения X(t) этой случайной функции для любого значения аргумента t.

Двумерным законом распределения случайной функции X(t) называется совместный закон распределения двух ее сечений [X(t₁) и X(t₂)] для любых значений t₁ и t₂.. Соответственно можно рассмотреть n – мерный закон распределения.

Математическим ожиданием случайной функции X(t) называется неслучайная функция m_x(t) которая при каждом значении аргумента t представляет собой математическое ожидание соответствующего сечения случайной функции:

m_x(t) = M[X(t)]

Случайная функция X(t) аргументом которой является время обычно называют случайным процессом. Случайный процесс протекающий в физической системе S состоит в том , что с течением времени система S случайным образом меняет свое состояние. Если состояние системы S описывается одной скалярной случайной величиной X(t) то это скалярный случайный процесс. Если состояние системы описывается несколькими случайными величинами то это векторный случайный процесс.

Случайный процесс, протекающий в системе S, называется процессом с дискретным временем, если переходы системы из одного состояния в другое возможны только в определенные, заранее известные моменты времени t₁, t₂, …

Случайный процесс, протекающий в системе S, называется процессом с непрерывным временем, если переходы системы из состояния в состояние могут происходить в любые, случайные моменты времени, непрерывно заполняющие ось Ot или ее участок.

Случайный процесс, протекающий в системе S называется процессом с дискретными состояниями если число возможных состояний системы конечно или счетно.

Случайный процесс, протекающий в системе S, называется процессом с непрерывными состояниями если множество возможных состояний системы несчетно.

Одномерным законом распределения случайной функции Х(t) называется закон распределения сечения X(t) этой случайной функции для любого значения аргумента t. Если случайная функция Х(t) непрерывна, то этот закон представляет собой плотность распределения сечения X(t) и обозначается f(x,t)

Математическим ожиданием случайной функции X(t) называется неслучайная функция m_x(t) которая при каждом значении аргумента t представляет собой математическое ожидание соответствующей случайной функции.

При прибавлении к случайной функции X(t) неслучайного слагаемого φ(t) к ее математическому ожиданию прибавляется то же неслучайное слагаемое.

При умножении случайной функции X(t) на неслучайный множитель φ(t) ее математическое ожидание умножается на тот же множитель.

Контрольные вопросы:

1. Что называют реализацией случайной функции?

2. Привести определение сечения случайной функции.

3. Какую случайную функцию называют случайным процессом?

4. Какие процессы называют процессами с дискретным временем?

5. Какие процессы называют процессами с непрерывным временем?

6. Какие процессы называют процессами с дискретными состояниями?