Системы случайных величин

Система двух случайных величин (Х,Y) геометрически интерпретируется как случайная точка с координатами (Х,Y) на плоскости x0y или как случайный вектор, направленный из начала координат в точку (Х,Y).

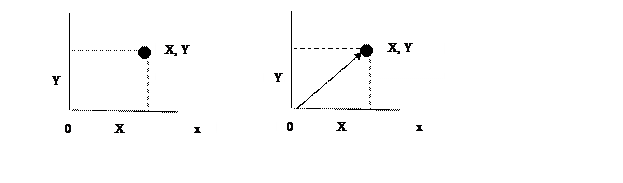
Система n случайных величин (Х₁, Х₂, . . . , Х_n) - случайная точка или случайный вектор в пространстве n измерений.

Совместной функцией распределения двух случайных величин (X,Y) называется вероятность совместного выполнения двух неравенств Х<x и Y<y:

F(x,y) = P{X<x, Y<y}

Геометрически F(x,y) интерпретируется как вероятность попадания случайной точки (X,Y) в квадрант с с вершиной (x,y).

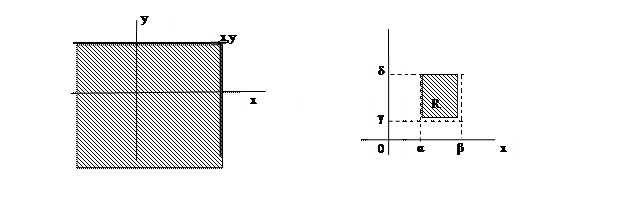
Вероятность попадания случайной точки (X,Y) в прямоугольник R со сторонами параллельными осям координат , включающий свою нижнюю и верхнюю границы, но не включающий свою верхнюю и правую выражается через функцию распределения формулой

P{(X,Y) 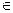R} = F(β,δ) – F(α,δ) – F(β,γ) +F(α,γ)

Совместная плотность двух непрерывных случайных величин представляет собой вторую смешанную производную частную производную функции распределения по обоим аргументам.

f(x,y) – ∂²F(x,y)/ ∂x∂y = F’’_xy(x,y)

Совместная функция распределения выражается через совместную плотность

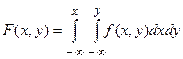
Плотности отдельных величин, входящих в систему выражаются через совместную плотность

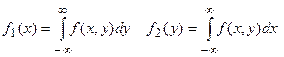
Условным законом распределения случайной величины входящей в систему называется закон ее распределения, вычисленный при условии, что другая случайная величина приняла определенное значение. Условные функции распределения случайных величин Х и Y , входящих в систему обозначаются F₁(x|y) и F₂(y|x) а условные плотности распределения f₁(x|y) и f₂(y|x).

Теорема умножения плотностей

f(x,y) = f₁(x)f₂(y|x) f(x,y) = f₂(y)f₁(x|y)

Случайные величины Х и Y называются независимыми если условный закон распределения одной из них не зависит от того какое значение примет другая:

f₁(x|y) = f₁(x) или f₂(y|x) = f₂(y)

Для независимых случайных величин теорема умножения плотностей примет вид

f(x,y) = f₁(x) f₂(y)

Корреляционный момент двух случайных величин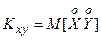

K_xy = M[X·Y] – M[X]·M[Y]

Для независимых случайных величин корреляционный момент равен 0.

Коэффициентом корреляции r_xy двух случайных величин Х и Y называется безразмерная величина

r_xy = K_xy/(σ_хσ_у) где σ_х= 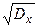σ_у=

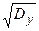
Случайные величины называются некоррелированными если их корреляционный момент равен 0. Из независимости случайных величин следует их некоррелированность. Обратное не верно.

Если случайные величины Х и Y связаны линейной зависимостью вида

Y = aX + b, где a и b не случайны то их коэффициент корреляции равен

r_xy = 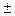1 где знак берется в соответствии со знаком коэффициента а.

Для любых двух случайных величин |r_xy|<1

Совместной функцией распределения двух случайных величин Х_1, Х₂, …Х_n называется вероятность совместного выполнения неравенств вида X_i<x_i

F(x₁,x₂, ….x_n) = P{X₁<x₁, X₂<x₂,…,X_n<x_n}

Совместной плотностью n случайных величин называется n-я смешанная частная производная функции распределения;

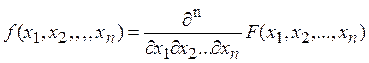
Если величины Х_1, Х₂, …Х_n независимы, то

f(x₁,x₂, ….x_n) = f₁(x₁) f₂(x₂)… f_n(x_n)

Вероятность попадания случайной точки Х_1, Х₂, …Х_n в пределы n-мерной области D выражается n=кратным интегралом

P{{( Х_1, Х₂, …Х_n) 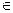D} = 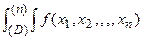dx₁….dx_n

Корреляционной матрицей системы n случайных величин ( Х_1, Х₂, …Х_n) называется таблица , составленная из корреляционных моментов всех этих величин, взятых попарно:

|K_ij| =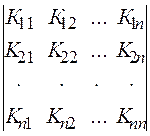

Где K_ij – корреляционный момент случайных величин X_i и X_j.

Корреляционная матрица симметрична поэтому обычно заполняется лишь половина таблицы:

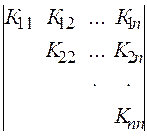
Нормированной матрицей системы n случайных величин называется таблица составленная из коэффициентов корреляции всех этих величин взятых попарно:

|r_ij| =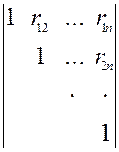

Где r_ij = K_ij/(σ₁σ₂) = коэффициент корреляции величин X_i и X_j.

Для случайных величин распределенных по нормальному закону некоррелированность равносильна независимости.

Контрольные вопросы:

1. Как геометрически интерпретируется система двух случайных величин?

2. Что называют совместной функцией распределения двух случайных величин?

3. Как геометрически интерпретируется функция распределения двух случайных величин F(x,y)

4. Как совместная плотность двух случайных величин выражается через совместную функцию распределения?

5. Как совместная функция распределения двух случайных величин выражается через совместную плотность?

6. Что называют условным законом распределения случайной величины, входящей в систему двух случайных величин?

7. Как выражается условная плотность вероятности через безусловную?

8. Какие случайные величины называют независимыми?

9. Что называют корреляционным моментом двух случайных величин?

10. Что называют совместной функцией распределения n случайных величин Х₁, Х₂, …Х_n ?