Числовые характеристики функций случайных величин

Одним из наиболее эффективных средств для решения вероятностных задач является аппарат числовых характеристик позволяющий находить характеристики случайных величин помимо их законов распределения . В частности чтобы находить числовые характеристики функций случайных величин, не надо знать законов распределения самих функций, достаточно знать закон распределения аргументов.

Если Х дискретная случайная величина с рядом распределения

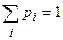
А величина Y связана с Х функциональной завимисомстью Y=φ(X), то математическое ожидание величины Y равно

m_y = M[φ(X )] = 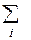φ(x_i)p_i

А дисперсия выражается любой из двух формул

D_y = D[φ(X )] = 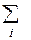[ φ(x_i) – m_y] ² p_i

D_y = 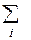[ φ(x_i)]² p_i – m_y ²

Если (X,Y) - система дискретных случайных величин, распределение которой характеризуется вероятностями

P_ij = P{X=x_i,Y=y_j}

А Z = φ(X,Y)

m_z = M[φ(X,Y )] = 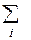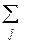φ(x_i,x_j)p_ij

А дисперсия выражается любой из двух формул

D_z = D[φ(X,Y )] = 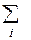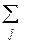[ φ(x_i,x_j) – m_z]² p_ij

D_z = 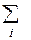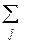[ φ(x_i,x_j)]² p_ij –m_z²

Если Х непрерывная случайная величина с плотностью f(x) а Y = φ(X)

То математическое ожидание величины Y равно

m_y = M[φ(X )] = 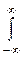φ(x)f(x)dx

а дисперсия выражается любой из двух формул:

D_y = D[φ(X )] = 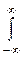[ φ(x) – m_y]² f(x)dx

D_y = 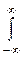[ φ(x)]² f(x)dx – m_y²

Если (Х, Y ) – система непрерывных случайных величин с совместной плотностью f(x,y) , а Z= φ(X,Y) то математическое ожидание величины Z равно

m_z = M[φ(X,Y )] = 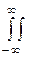φ(x,y)f(x,y)dxdy

а дисперсия выражается любой из двух формул:

D_z = D[φ(X,Y )] = 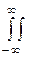[ φ(x,y) – m_z]² f(x,y)dxdy

D_z = D[φ(X,Y )] = 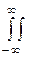[ φ(x,y)]²f(x,y)dxdy – m_z²

В ряде случаев не надо знать закон распределения аргументов, достаточно знать их числовые характеристики. Основные теоремы о числовых характеристиках.

1. Если с не случайная величина то

M[c] = c D[c] =0

2.Если с не случайная величина а Х – случайная , то

M[cХ] = cM[x] D[cX] =c²D[X]

1. Теорема сложения математических ожиданий:

M[X+Y] = M[X] + M[Y]

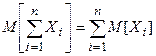
2. Математическое ожидание линейной функции нескольких случайных величин

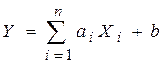
Где a_i и b не случайные коэффициенты, равно той же линейной функции от их математических ожиданий:

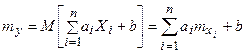
Где 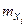= M[X_i]

5. Математическое ожидание произведения двух случайных величин Х и Y выражается формулой

M[XY] = M[X]M[Y] + K_xy

Где K_xy – корреляционный момент величин Х и Y. Эту формулу в другом виде можно записать так

K_xy = M[XY] - m_xm_y

6.Теорема умножения математических ожиданий. Математическое ожидание произведения двух некоррелированных случайных величин Х,Y равно произведению их математических ожиданий

M[XY] = M[X]M[Y]

7. Если Х_1, Х₂, …Х_n независимые случайные величины, то математическое ожидание их произведений равно произведению математических ожиданий.

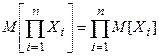
8. Дисперсия суммы двух случайных величин выражается формулой

D[X+Y] = D[X] + D[Y] +2 K_xy

9. Дисперсия суммы нескольких случайных величин выражается формулой:

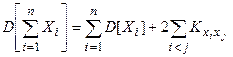где 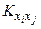- корреляционный момент случайных величин Х_i , X_j

10. Теорема сложения дисперсий . Дисперсия суммы двух некоррелированных случайных величин Х, Y равна сумме их дисперсий:

D[X+Y] = D[X] + D[Y]

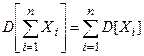
11. Дисперсия линейной функции нескольких случайных величин

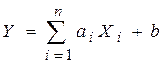,ге a_i и b не случайные коэффициенты выражается формулой

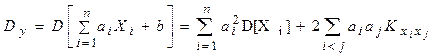
В случае если величины Х_1, Х₂, …Х_n некоррелированны

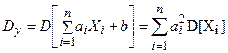
Контрольные вопросы:

1. Чему равно математическое ожидание величины Y если Х дискретная случайная величина, а Y связано с Х зависимостью Y=φ(X) ?

2. Какими формулами выражается дисперсия величины Y , связанной с дискретной величиной Х зависимостью Y=φ(X) ?

3. Чему равно математическое ожидание величины Y если Х непрерывная случайная величина, а Y связано с Х зависимостью Y=φ(X) ?

4. Какими формулами выражается дисперсия величины Y , связанной с непрерывной величиной Х зависимостью Y=φ(X) ?

5. Сформулировать теорему сложения математических ожиданий.

6. Чему равно математическое ожидание произведения двух случайных величин?

7. Сформулировать теорему умножения двух некоррелированных случайных величин.

8. Сформулировать теорему сложения дисперсий для двух некоррелированных случайных величин.