Способы определения современной стоимости денег и наращенной суммы вложений

Финансовые операции могут совершаться с использованием простых и сложных процентов.

При использовании простых процентов наращенная сумма рассматривается с учетом того, что проценты на проценты не начисляются, а начисляются на одну и туже исходную сумму. В этом случае алгоритм расчета наращенной суммы будет таким:

St=S₀*(1+I*t), где

St – наращенная сумма

S₀ – исходная сумма

i – годовая процентная ставка

t – число периодов начисления.

Из этой формулы можно рассчитать исходную сумму:

.

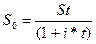При расчете числа простых процентов выплачиваемых банком используется алгоритм:

.

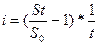Пример: в банк положены 5 тыс. руб. на срок 2 года. Ставка простых процентов 10 % в год. Определить наращенную сумму через 2 года.

S₀=5000

i=10%=0.1

t=2

St=5000*(1+0.1*2)=6 тыс. руб.

Следует обратить внимание, что кредитору выгоднее давать ссуду не под простой процент, а под простой дисконт.

Простой дисконт представляет собой процентный доход, который вычитается из ссуды в момент ее выдачи:

.

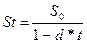Сравним наращенную сумму, которую надо вернуть кредитору при условии выдачи кредита в одинаковой сумме, но под простой процент в одном случае и под простой дисконт в другом.

Предположим, что ссуда в размере 20 тыс. руб. выдана сроком на 1 год под 20 % годовых, простой дисконт так же составляет 20%.

S₀=20000

i=20%=0.2

d=20%=0.2

t=1

St=S₀*(1+I*t)=20000*(1+0.2*1)=24000 руб.

Если ссуда получена под простой дисконт при прочих равных условиях, то вернуть надо будет большую сумму.

St= 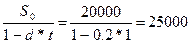руб.

И так чтобы получить на руки кредит в сумме 20 тыс. руб. под простой дисконт надо задолжать кредитору большую сумму.

На практике финансовые операции обычно совершаются с использованием сложных процентов. Особенности процесса при этом состоят в том, что исходная базовая сумма увеличивается с каждым периодом начисления (в то время как при использовании простых процентов она остается неизменной). В данном случае наращенная сумма исчисляется по алгоритму:

St=S₀*(1+I)^t

Пример: банк ежегодно начисляет сложные проценты (20%) на вклад в сумме 150 тыс. руб. Тогда наращенная сумма через два года составит:

St=150000*(1+0,2)²=216000 руб.

Ставка сложных процентов обычно указывается на год, хотя начисляться они могут и чаще (в полугодии, в квартал, месяц и т.д.). в этом случае алгоритм расчета наращенной суммы выглядит так:

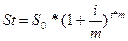, где

m – число раз начисления процентов в году.

Если ввести в предыдущий пример условие, что годовая ставка сложных процентов применяется четыре раза в году, то наращенная сумма составит:

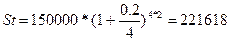руб.

Для определения современного значения долга, если известна его полная сумма через несколько лет и условия начисления сложных процентов используется алгоритм дисконтирования

; .

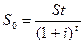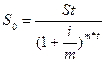Например: рассчитать современное значение долга, если его полная сумма через 3 года составит 20 тыс. руб., а проценты начисляются в конце каждого года по ставке 30%

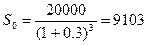руб.

Если проценты начисляются в конце каждого полугодия исходя из годовой номинальной ставки 30%, тогда:

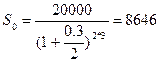руб.

В финансовых расчетах так же необходимо учитывать инфляцию, тем более если она значительна.

С одной стороны сумма положенная на депозит получит приращение, а с другой утратит свою реальную стоимость в результате инфляции.

Для определения наращенной суммы с учетом инфляции используют алгоритм:

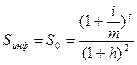, где

h – ожидаемый месячный темп инфляции.

Разница между наращенной суммы с учетом инфляции и базовой суммы, показывающая уменьшение реальной стоимости суммы, положенной на депозит называется эрозией капитала:

ЭК=S_инф-S₀