Комплексные системы

Системы РА, которые формируются не только на базе радиотехнических устройств, но и на базе устройств других типов (например, гироскопических приборов, инерциальных систем и др.), называют комплексными. Подобные системы широко применяются при навигации для определения координат и параметров движения различных объектов (например, для измерения скорости летательного аппарата и угла сноса относительно расчетной траектории используется гироскопическая система с доплеровским измерителем). Для измерения высоты полета применяются барометрический и радиолокационный высотомеры. Для комплексной системы РА характерно наличие нескольких параллельно работающих каналов с различными датчиками измерения одной и той же информации. На рис. 7.11 показана типовая структурная схема комплексной измерительной системы, в которой входной сигнал 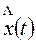измеряется разнотипными датчиками Д₁, Д₂, ..., Д_n с передаточными функциями W_дi(p), где i=l, 2, ..., n; воздействия V_i(t) учитывают погрешности датчиков. Комплексирование системы заключается в вычислении оценки x(t) с точностью, превышающей достижимую при раздельном использовании датчиков. Из схемы (рис. 7.11) следует, что преобразование Лапласа для оценки входного сигнала будет иметь вид

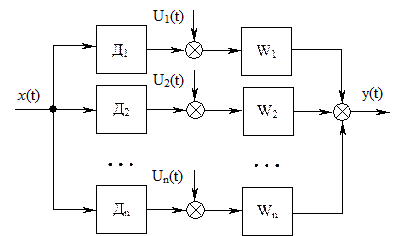
Рис. 7.11 - Типовая структурная схема комплексной измерительной

системы РА

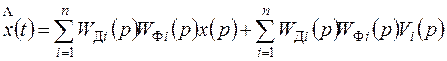. (7.57)

Преобразование Лапласа для сигнала ошибки имеет вид

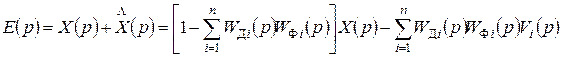. (7.58)

Из последнего выражения следует, что если передаточные функции каналов системы выбирают из условия

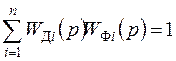, (7.59)

то выражения (7.57) и (7.58) принимают вид

;

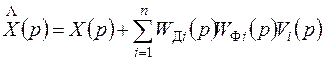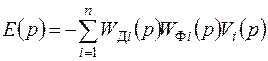. (7.60)

Таким образом, ошибка комплексной системы не зависит от характеристик измеряемого сигнала и определяется только погрешностями датчиков.

Равенство (7.59) называют условием инвариантности, а систему, в которой удается его реализовать, – инвариантной относительно ошибки измеряемого сигнала.

Условие инвариантности накладывает ограничения только на суммарную передаточную функцию, но не на передаточные функции отдельных каналов, поэтому при синтезе комплексной системы остается некоторая свобода выбора передаточных функций отдельных каналов, что позволит уменьшить ошибку из-за погрешностей датчиков.

Необходимо отметить, что условие инвариантности (7.59) в динамических системах удается выполнить лишь приближенно, поэтому в реальной системе динамическая ошибка не равна нулю (она может быть значительно уменьшена по сравнению с ошибками измерения при использовании одного канала измерения).

Следует также иметь в виду, что рассмотренная система, которую принято называть многоканальной схемой фильтрации, чувствительна к отклонению параметров устройств от расчетных значений, поэтому при проектировании таких систем необходимо обеспечить стабильность параметров ее звеньев.

Рассмотрим еще один класс комплексных систем РА, основой которых является обычная система РА с обратной связью, а сигнал с нерадиотехнического датчика, с помощью которого измеряется управляющее воздействие x(t), вводится в замкнутый контур после дискриминатора (рис. 7.12). В таких системах удается значительно повысить точность системы РА относительно управляющего воздействия без ухудшения средней квадратической ошибки из-за действия помех.

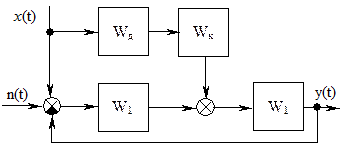
Рис. 7.12 - Структурная схема комплексной системы РА

Из рис. 7.12 следует, что преобразование Лапласа для выходного сигнала будет иметь вид

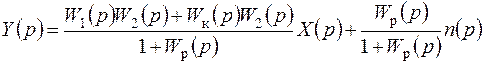; (7.61)

для ошибки системы

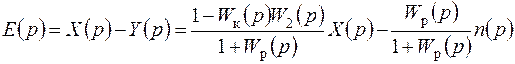. (7.62)

Если выполняется условие инвариантности

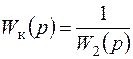, (7.63)

то выражения (7.61) и (7.62) принимают вид

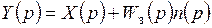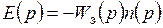; , (7.64)

где W_з(p) – передаточная функция замкнутого контура системы РА.

Из выражений (7.64) следует, что ошибка относительно управляющего воздействия равна нулю или инвариантна относительно этого сигнала. Путем выбора цепи сигнала ошибки системы с передаточной функцией W₁(p) нетрудно сформировать замкнутый контур системы с учетом требуемой фильтрации помех.

Датчик, измеряющий управляющее воздействие, и последовательно включенный с ним фильтр с передаточной функцией W_к(р) образуют цепь компенсации комплексной системы РА. Эта цепь не формирует замкнутого контура, а следовательно, не влияет на устойчивость комплексной системы.

При реализации условия инвариантности (7.63) в реальных системах степень полинома числителя передаточных функций устройств всегда меньше степени полинома их знаменателя, поэтому функция (7.63) не удовлетворяет условию физической реализуемости и в данной системе РА инвариантность ошибки относительно управляющего воздействия недостижима. Однако в подобных системах можно существенно повысить точность относительно управляющего воздействия при необходимой фильтрации помех, т.е. сделать системы широкополосными относительно управляющего сигнала и узкополосными относительно помехи.

Синтез комплексных систем РА можно выполнить с учетом следующих условий: 1) обеспечения нужных частотных характеристик системы; 2) повышения ее динамической точности работы. Проанализируем метод, который позволит повысить порядок астатизма в комплексной системе относительно управляющего воздействия по сравнению с порядком астатизма замкнутого контура. Передаточная функция ошибки системы, как следует из выражения (7.62), имеет вид

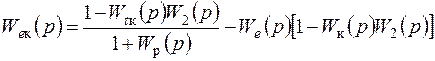, (7.65)

где W_e(p) – передаточная функция ошибки замкнутого контура.

Разложим передаточную функцию ошибки комплексной системы (7.65) в степенной ряд:

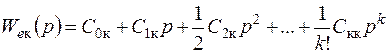. (7.66)

Аналогичным образом представим и второй сомножитель выражения (7.65):

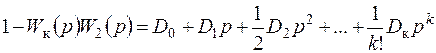. (7.67)

Тогда передаточная функция ошибки комплексной системы с учетом выражения (6.8) примет вид

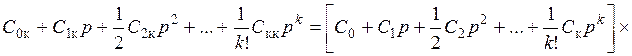
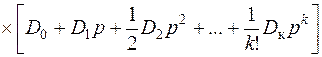, (7.68)

где C_i, i = 0, 1, …, k – коэффициенты ошибок передаточной функции ошибки замкнутого контура системы.

Приравняв в последнем выражении слагаемые при одинаковых степенях р, найдем коэффициенты ошибок комплексной системы:

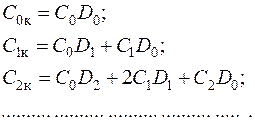(7.69)

Из формул (7.69) следует, что необходимый порядок астатизма обеспечивается, если соответствующее число коэффициентов D_i (весовой коэффициент) равно нулю. Из этих условий и определяется выражение для передаточной функции компенсации комплексной системы.

Подставим выражения

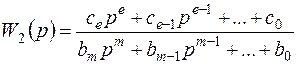; (7.70)

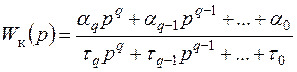(7.71)

в формулу (7.67). Тогда для получения астатизма первого порядка необходимо, чтобы передаточная функция цепи компенсации была равна

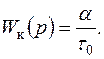(7.72)

Коэффициенты этой функции определим из условия

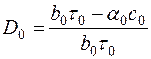. (7.73)

Для получения астатизма второго порядка нужно, чтобы передаточная функция цепи компенсации была равна

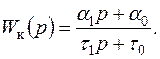(7.74)

Коэффициенты функции найдем из условия (7.73) при

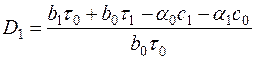. (7.75)

При последовательном определении коэффициентов передаточной функции (7.71) одни коэффициенты, например t_i, выбирают из условия обеспечения требуемых характеристик комплексной системы, а коэффициенты a_i вычисляют согласно равенству нулю соответствующих коэффициентов D_i.

Коэффициенты t_i передаточной функции цепи компенсации определяют инерционность цепи компенсации. Для выяснения их влияния на частотные характеристики представим передаточную функцию комплексной системы в виде

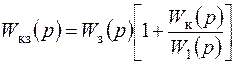. (7.76)

Следовательно, наличие цепи компенсации в комплексной системе эквивалентно последовательному включению с замкнутым контуром корректирующего устройства с передаточной функцией

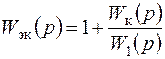. (7.77)

Из выражения (7.77) следует, что чем меньше инерционность цепи компенсации, тем больший опережающий эффект создается корректирующим устройством. При этом полоса пропускания комплексной системы РА относительно управляющего воздействия увеличивается.

Пример. Найти передаточную функцию цепи компенсации для системы автоматического сопровождения цели РЛС, рассмотренной в примере 7.1, если порядок астатизма в системе относительного воздействия, возникающего из-за колебаний летательного аппарата, равен двум.

Решение. Систему сформируем по схеме (рис. 7.12), в которой передаточные функции определяются выражениями

;

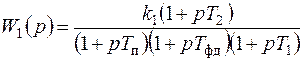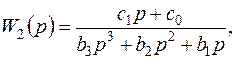
где ; ; ; ;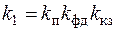

; .

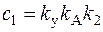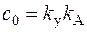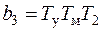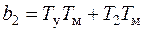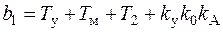Воздействие, возникающее из-за колебаний летательного аппарата, измеряется гироскопическим датчиком угловой скорости, сигнал с которого является входным сигналом цепи компенсации.

Замкнутый контур рассматриваемой системы имеет первый порядок астатизма, поэтому для получения в комплексной системе астатизма второго порядка необходимо, как это следует из формул (7.69), чтобы коэффициент Д_о в разложении (7.67) был равен нулю. Для этого нужно, чтобы передаточная функция цепи компенсации была реализована в соответствии с (7.74). Параметры цепи вычисляются из условия 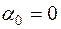, 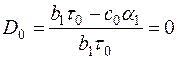. Из последнего выражения находим, что 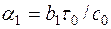. Пусть t₁=0,01 с для того, чтобы полоса пропускания системы относительно воздействия, возникающего из-за колебаний летательного аппарата, была больше полосы пропускания замкнутого контура. При расчетных значениях параметров системы автоматического сопровождения, найденными в примере 7.1, передаточная функция цепи компенсации

.

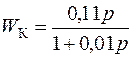Данная передаточная функция может быть реализована RС-цепью и усилителем с коэффициентом усиления, равным 11. Дальнейшее уменьшение коэффициента T₁ с целью большего расширения полосы пропускания нецелесообразно, так как приводит к увеличению коэффициента усиления в цепи компенсации.

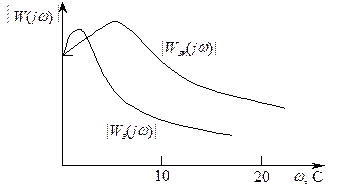
Рис. 7.13 - АЧХ комплексной системы РА

На рис. 7.13 показаны АЧХ замкнутого контура |W_з(jw)| и комплексной системы |W_зк(jw)|, из которых видно, что введение цепи компенсации расширило полосу пропускания относительно воздействия, обусловленного колебаниями летательного аппарата, до 37 с^–1.

ЛИТЕРАТУРА

1. Теория автоматического управления / Под ред. А.В. Нетушила. Учебник для вузов. Изд. 2-е, доп. и перераб. – М.: Высшая школа, 1976.

2. Коновалов Г.Ф. Радиоавтоматика. Учеб. для вузов по спец. «Радиотехника». – М.: Высш. шк., 1990. – 335 с.

3. Первачев С.В., Валев А.А., Чиликина В.М. Статистическая динамика радиотехнических следящих систем. – М.: Сов. Радио, 1973. – 488 с.

4. Макаров И.М., Менский Б.М. Линейные автоматические системы (элементы теории, методы расчета и справочный материал). Учебное пособие для вузов. – М.: Машиностроение, 1977. – 464 с.

5. Проектирование радиоприемных устройств / Под ред. А.П. Сиверса. Учебное пособие для вузов. – М.: Сов. Радио, 1976. – 488 с.

6. Жаркой А.Г., Туев В.И. Радиоавтоматика. Руководство к лабораторным работам для студентов специальности 2301. Часть 2. - Томск: Ротапринт ТИАСУРа, 1988. – 27 с.

7. Коновалов Г.Ф., Коноваленко О.В. Системы автоматического управления с электромагнитными порошковыми муфтами. – М.: Машиностроение, 1976.

8. Радиоавтоматика / Под ред. В.А. Бесекерского. – М.: Высшая школа, 1985.