Синтез систем с неполной информацией о воздействиях

Ранее, при динамическом синтезе систем РА полагали, что характеристики управляющих воздействий и помех известны, т.е. заданы их математические ожидания и спектральные плотности случайных составляющих.

На практике это не всегда так. Характеристики воздействий обычно известны не полностью. Кроме того, они изменяются в процессе работы системы, поэтому показатели качества работы могут оказаться ниже расчетных.

Построение систем РА с использованием адаптивных систем позволяет исключить зависимость показателей качества работы от изменения характеристик воздействия и нестабильности параметров устройств. На практике используют так называемые робастные системы (от английского слова robust – грубый). Техническая реализация таких систем РА, по сравнению с адаптивными системами, намного проще, что является их существенным преимуществом.

Синтез робастных систем может быть выполнен различными методами. Применительно к задачам синтеза систем РА целесообразно использовать метод, основанный на известных средних квадратических значениях управляющего воздействия и его производных. Данный метод не связан с конкретной формой спектральной плотности управляющего сигнала, поэтому ее изменение не приводит к несоблюдению точности работы системы РА.

Рассматриваемый метод синтеза систем РА сводится к выбору частотной характеристики ошибки из условия непревышения средней квадратической ошибкой заданного значения. После этого можно сформулировать требования к частотной характеристике разомкнутой системы.

Дисперсия ошибки относительно управляющего воздействия в соответствии с выражением (6.22) определяется как

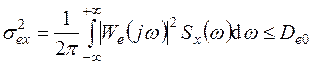, (7.43)

где W_е(jw) – частотная характеристика ошибки; D_e0 – допустимое значение дисперсии ошибки.

Представим квадрат АЧХ ошибки в следующем виде:

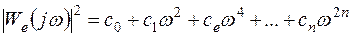. (7.44)

Тогда дисперсия ошибки (7.43)

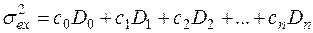, (7.45)

где D₀ – дисперсия управляющего воздействия; D₁ – дисперсии производных; с_i – постоянные коэффициенты.

Задача синтеза системы состоит в выборе характеристики W_е(jw), удовлетворяющей условию (7.43). Если известна только дисперсия управляющего воздействия D₀, то из выражения (7.45) следует, что с₀ = D_e0/D₀ и частотная характеристика ошибки проектируемой системы должна удовлетворять условию

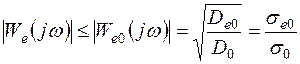, (7.46)

где |W_е0(jw)| – АЧХ ошибки, составленная по априорным сведениям об управляющем воздействии.

Таким образом, ошибка не должна превышать значения (7.46) в диапазоне частот, в котором возможны спектральные составляющие управляющего воздействия.

В том случае, если известна только дисперсия первой производной управляющего воздействия D₁, то с₁ = =D_е0/D₁ и частотная характеристика ошибки проектируемой системы должна удовлетворять условию

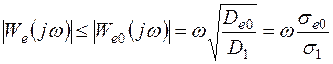. (7.47)

Если известна только дисперсия второй производной управляющего воздействия, то

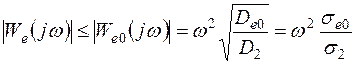. (7.48)

От ограничений, накладываемых на АЧХ ошибки, можно перейти к требованиям, которым должна удовлетворять частотная характеристика разомкнутой проектируемой системы. Из выражений (4.30) и (4.34) следует, что

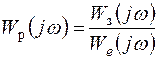. (7.49)

Так как на частотах меньше частоты среза |W_з(jw)| » 1, то условия (7.46) – (7.48) выполняются, если

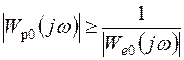, (7.50)

а ФЧХ разомкнутой системы может быть произвольной.

На частотах больше частоты среза |W_з(jw)| » |W_р(jw)| и поэтому вид частотной характеристики разомкнутой системы не влияет на точность системы РА и может быть произвольным, но при этом требования к запасам устойчивости должны соблюдаться.

Выполнение условия (7.50) гарантирует, что динамическая ошибка будет не выше заданной.

Очевидно, что выражениям (7.46) и (7.50) (рис. 7.9) соответствует прямая линия, параллельная оси частот и отстоящая от нее на 20 lg s₀/s_e0, условиям (7.47) и (7.50) – прямая с наклоном – 20 дБ/дек, которая пересекает ось абсцисс на частоте, равной s₁/s_e0, а условиям (7.48) и (7.50) – прямая с наклоном – 40 дБ/дек, которая начинается на оси абсцисс с частоты . Эти прямые образуют запретную область, в которой не должна располагаться низкочастотная часть логарифмической АЧХ разомкнутой проектируемой системы РА. Частоты, соответствующие точкам излома запретной области, вычисляют по формулам

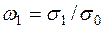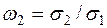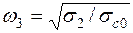; ; . (7.51)

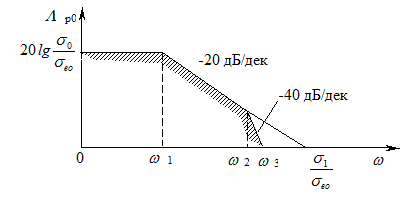
Рис. 7.9 - ЛЧХ запретной области относительно динамической ошибки

Рассмотрим ограничения на вид АЧХ разомкнутой проектируемой системы из-за действия помехи, спектральная плотность которой известна и постоянна в пределах полосы пропускания системы РА (помеха в виде белого шума). Тогда дисперсия ошибки из-за действия помехи определяется в виде

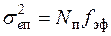, (7.52)

где f_эф – эффективная полоса пропускания системы;

N_п – уровень спектральной плотности белого шума помехи.

Задача синтеза системы РА заключается в том, чтобы суммарная средняя квадратическая ошибка системы не превышала допустимого значения:

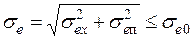, (7.53)

где s_еп – средняя квадратическая ошибка из-за действия помехи.

Условие (7.53) накладывает противоречивые требования к проектируемой системе РА. С одной стороны, средняя квадратическая ошибка относительно сигнала должна быть меньше s_е0, так как в противном случае не будет выполнено условие (7.53), а с другой – не должна превышать этого значения и составляющая ошибки s_еп. Поэтому эффективная полоса пропускания проектируемой системы определяется неравенством

. (7.54)

Таким образом, при синтезе системы РА необходимо обеспечить одновременное удовлетворение условий (7.50) и (7.54). Если эти условия выполнить одновременно невозможно, то при заданном значении s_е0 решения задачи проектирования робастной системы РА не существует.

Определим, какие ограничения накладывает условие (7.54) на АЧХ разомкнутой системы. С этой целью рассмотрим типовую логарифмическую АЧХ, низкочастотные участки которой содержат асимптоты с наклонами –20, –40 или –60 дБ/дек. При этом, всегда в области частоты среза наклон логарифмической АЧХ равен –20 дБ/дек, так как только в этом случае можно обеспечить необходимый запас устойчивости по фазе.

В [8] показано, что для систем РА с такими наклонами логарифмической АЧХ разомкнутой системы эффективная полоса пропускания системы с достаточной для практики точностью определяется по формуле

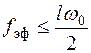, (7.55)

где w₀ – частота, соответствующая точке пресечения асимптоты логарифмической АЧХ с наклоном –20 дБ/дек с осью абсцисс; l – коэффициент, равный1, 2 или 3, в зависимости от наклона асимптоты, для которой определена частота w₀. Согласно (7.54) и (7.55),

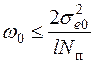. (7.56)

Это выражение определяет крайнее допустимое положение логарифмической АЧХ разомкнутой проектируемой системы РА, т.е. границу запретной области, в которой не должна располагаться логарифмическая АЧХ разомкнутой системы. Построение запретной области осуществляется следующим образом. На оси абсцисс (рис. 7.10) через точку 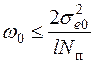проводят прямую с наклоном –20 дБ/дек, а через точки w_о/2 и w_о/3 прямые с наклонами –40 и –60 дБ/дек. В результате формируется запретная область, заштрихованная на рис. 7.10, а.

Требования к точности работы проектируемой системы РА относительно возмущающего воздействия выполняются, если ее логарифмическая АЧХ не заходит в запретную область.

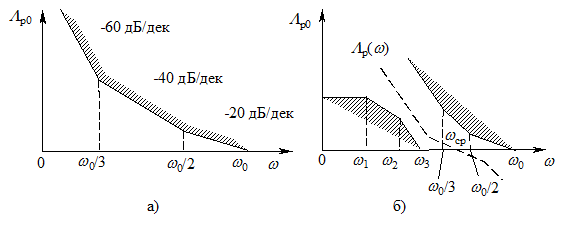
Рис. 7.10 - ЛЧХ запретной области относительно возмущающего

воздействия (а) и ЛЧХ общей запретной области (б)

На рис. 7.10, б показаны две запретные области, определенные ранее. Для обеспечения в проектируемой системе РА заданной точности необходимо, чтобы выбранная логарифмическая АЧХ разомкнутой системы не располагалась в запретных областях и удовлетворяла требованиям к запасам устойчивости. На рис. 7.10, б такая характеристика показана пунктиром. Если запретные области на рис. 7.10, б перекрываются, то синтез робастной системы при заданных точностных характеристиках невозможен. Для гарантированного получения заданной точности должен быть обеспечен некоторый интервал между левой и правой запретными областями. Минимальная ширина этого интервала должна составлять около четверти декады.