Типовые примеры и методы их решения

Пример 1.5.1. Предприятие получило следующие кредиты под разные простые процентные ставки: 36 тыс. руб. на 240 дней под 35% годовых; 28 тыс. руб. на 150 дней под 32% годовых; 60 тыс. руб. на 100 дней под 38% годовых; 52 тыс. руб. на 80 дней под 34% годовых. Определите: а) средний срок кредита; б) среднюю процентную ставку; в) средний срок и среднюю процентную ставку одновременно; г) среднюю величину кредита.

Решение. а) Вначале сделаем некоторые замечания по поводу использования формулы (32), представляющей один из вариантов определения среднего срока кредита. Конечно, в формуле периоды n_k измеряются в любых единицах времени (годы, кварталы, месяцы, дни и т.д.), согласованных с размерностями соответствующих процентных ставок i_k (годовые, квартальные, месячные, дневные и т.д.). Однако вид формулы (32) позволяет определять средний срок, не особенно заботясь о согласовании размерностей исходных сроков и процентных ставок. Так, если, например, сроки n_k даны в днях (вообще в любых, но единых для всех сроков единицах времени), а i_k представляют собой годовые процентные ставки, то, не занимаясь переводом n_k в годы, по формуле (32) сразу получаем средний срок 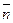в днях. Аналогичные соображения можно высказать и в связи с применением формул (30), (34), (36).

Полагаем P₁ = 36 тыс. руб., Р₂ = 28 тыс. руб., P₃ = 60 тыс. руб., P₄ = 52 тыс. руб. Несмотря на то что i₁ = 0,35; i₂ = 0,32; i₃ = 0,38 и i4as 0,34 – годовые процентные ставки, в соответствии со сказанным выше, средний срок будем измерять в днях, а исходные сроки переводить в годы не будем, т.е. n₁ = 240 дней, n₂ = 150 дней, n₃ = 100 дней, n₄ = 80 дней. По формуле (32) получим:

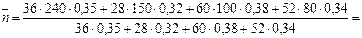
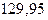дня,

т.е. n = 130 дней.

Если же срок каждого кредита измерять в годах, считая, что в году 360 дней, то n₁ = 0,667 года, n₂ = 0,417 года, n₃=0,278 года, n₄ = 0,222 года и

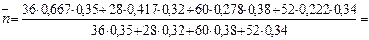
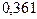года,

или 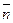= 0,361•360 = 129,96 дня, т.е. 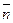= 130 дней. Естественно, получили тот же самый результат.

Для проверки правильности результата найдем начисляемые проценты на каждый кредит при исходных сроках, считая в году 360 дней, и сложим эти проценты:

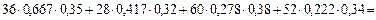
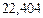тыc. руб.

Теперь найдем сумму процентов при замене всех сроков на средний срок:

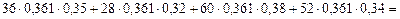
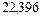тыс. руб.

Таким образом, получили (в пределах точности вычислений) одну и ту же сумму - 22,4 тыс. руб. Если исходный срок каждого кредита в годах взять с большим количеством знаков после запятой, то сумма начисляемых процентов на каждый кредит при исходных сроках составит 22,396 тыс. руб.

Формулу (32) можно записать и таким образом:

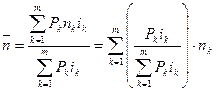
т.е. средний срок равен взвешенной сумме исходных сроков, где весом для каждого срока п_k служит доля произведения 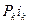, которую оно составляет от общей суммы 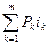, причем очевидно, что сумма всех весов обязательно равна единице. Выполняя вычисления для данного случая, получим:

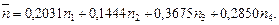
Конечно, 0,2031 + 0,1444 + 0,3675 + 0,2850 = 1. Заметим, что из-за приближенных вычислений сумма весов может незначительно отличаться от единицы.

б) Как и в пункте а), измеряя сроки в днях, воспользуемся формулой (30):

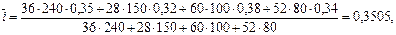или 35,05%.

Записывая формулу (30) таким образом:

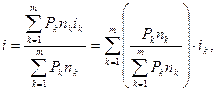
получаем представление 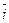в виде взвешенной суммы процентных ставок. Для нашего случая:

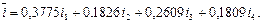
Обратим внимание на тот факт, что, применяя формулы (29), (30), (33) и (34), ставки можно выражать как в десятичных дробях, так и в процентах. Это утверждение следует из вида формул. Если, в частности, исходные ставки даны в процентах, то в результате применения формул соответствующие ставки сразу будут выражены в процентах.

в) В этом случае нельзя одновременно применять формулы (30) и (32). Можно показать, что если средний срок кредита рассчитывается по формуле (32), то среднюю процентную ставку надо рассчитывать по формуле (29). А если средняя процентная ставка находится по формуле (30), то средний срок кредита надо находить по формуле (31). Обычно время учитывается при расчете среднего срока кредита. Следовательно, воспользуемся формулами (32) и (29). По формуле (32) 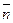=130 дней, а по формуле (29):

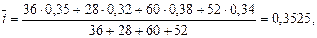
т.е. отличается от 35,05% - средней процентной ставке, найденной в предыдущем пункте. Заметим, что, применяя формулу (29), мы фактически решаем следующую задачу: найти среднюю процентную ставку, когда кредиты выданы на одинаковый срок (130 дней).

Если бы применяли формулы (30) и (31), то 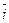= 35,05% и 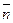= 130,68 дней или 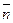=131 день.

По существу задача одновременного определения среднего срока кредита и средней процентной ставки имеет бесчисленное множество решений, так как величины 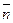и 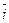можно находить просто ю равенства начисленных процентов:

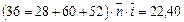, т.е. .

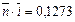Определяя подходящим образом 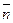, находим 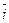(или наоборот). Только надо учитывать соответствие размерносте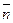й и 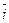. Так, если 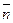измеряется в годах, то 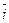- годовая процентная ставка; если 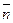измеряется в днях, то 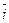- дневная процентная ставка и т.п. Например, пусть 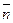=130 дней, тогда

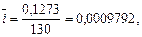
т.е. 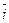= 0,09792 % в день, или, умножая на 360, получаем 35,25% в год.

г) Среднюю величину кредита 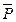можно определить по формуле, аналогичной формулам (30) и (32):

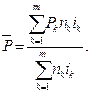
Подставляя вместо букв численные значения, находим, что 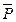=40,884 тыс. руб.

Подобным образом, как и в предыдущем пункте, можно одновременно находить среднюю величину кредита и среднюю процентную ставку или одновременно находить среднюю величину кредита и средний срок, но эти задачи на практике встречаются реже, чем задача определения среднего срока и средней процентной ставки.

В разобранном примере значения средней процентной ставки, найденной по различным формулам, не отличались значительно друг от друга. Но так бывает не всегда.

Пример 1.5.2. Выданы следующие кредиты под простые процентные ставки: 340 тыс. руб. на 1 день под 20% годовых и 1 тыс. руб. на 340 дней под 40% годовых. Сравните между собой средние процентные ставки, определенные разными способами.

Решение. Пусть P₁= 340 тыс. руб., Р₂ = 2 тыс. руб., n₁ = 1 день, n₂ = 340 дней, i₁ = 0,3, i₂ = 0,4 .

Если воспользоваться формулой (29), то:

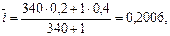
а если применить формулу (30), то:

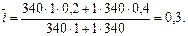
Таким образом, 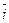, найденное по формуле (29), практически совпадает с одной из исходных процентных ставок i₁ = 20%; а 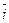, найденное по формуле (30), является средним арифметическим ставок i₁ = 20% и i₂ = 40% . Это хорошо видно из представления средней ставки в виде взвешенной суммы исходных ставок:

а) для формулы (29) 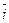= 0,9971i₁, + 0,0029 i₂;

б) для формулы (30) 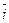= 0,5 i₁ + 0,51i₂.

Пример 1.5.3.Заемщик взял 27 января у одного кредитора под одну и ту же простую процентную ставку в 40% суммы в размере 10 тыс. руб., 6 тыс. руб., 20 тыс. руб. и 16 тыс. руб. со сроками погашения соответственно 1 марта, 14 мая, 25 июня и 18 августа того же года. Определите средний срок погашения всех ссуд и сумму, которую заемщик должен будет отдать кредитору, если в расчет принимаются точные проценты с точным числом дней и согласно соглашению для кредитора важно только то, чтобы величина начисленных процентов оставалась неизменной. Год невисокосный.

Решение. Всего заемщик взял у кредитора сумму в 52 тыс. руб. Считая, что на эту сумму сразу начисляются проценты и так как i₁ = i₂ = i₃ = i4 = 0,4, по любой формуле для определения средней процентной ставки получим 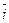= 0,4.

Несмотря на то что процентные ставки i₁, i₂, i₃, i₄ являются годовыми, в соответствии со сделанными выше замечаниями средний срок погашения всех ссуд будем измерять в днях и отсчитывать от дня первого планового платежа, т.е. n₁ = 0, n₂ =74, n₃ =116, n₄ =170. Взятые суммы измеряем в тыс. руб.: Р₁ =10, P₂ =6, P₃ =20, P₄ =16. Следовательно, сразу воспользовавшись формулой (31), являющейся в этой ситуации частным случаем формулы (32), получаем:

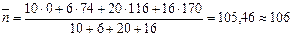дней.

Отсчитывая от 1 марта 106 дней, получим 15 июня - дату, когда заемщик может отдать единовременно Весь долг.

Поскольку кредитор выдал суммы 27 января, найдем, что 15 июня заемщик должен отдать долг в размере:

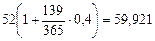тыс. руб.

Если бы в расчет принимались обыкновенные проценты с точным числом дней, то средний срок погашения ссуды остался бы тот же (т.е. 15 июня - дата единовременного возврата долга), однако размер возвращаемой суммы, естественно, увеличился:

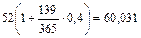тыс. руб.

Пример 1.5.4. Банк собирался выдать ссуды в размере 15 тыс. руб., 25 тыс. руб. и 20 тыс. руб. на сроки соответственно 2, б и 9 месяцев под простые ставки 36,40 и 44% годовых, причем проценты удерживались сразу. Под какую единую ставку банк согласится выдать эти ссуды, если он намерен взыскать при выдаче ссуд ту же величину процентов, как в первоначальном контракте с клиентом? Чему будет равен средний срок ссуды при таком изменении контракта?

Решение. Так как банк сразу удерживает проценты, то клиент на руки получает меньшую по величине ссуду, чем объявлено банком. Например, при ссуде 20 тыс. руб. на 9 месяцев под простую ставку 44% годовых клиент получает 20 (1-0,75^. 0,44) =13,4 тыс. руб. и должен будет вернуть банку через 9 месяцев 20 тыс. руб., т.е. на сумму 13,4 тыс. руб. в течение полугода фактически происходит наращение по простой учетной ставке 40%. Таким образом, при определении новой ставки можно воспользоваться формулой (34) определения среднего значения простой учетной ставки.

Измеряя ссуды в тыс. руб., а сроки - в месяцах, полагаемf₁ =15, F₂= =25, f₃ =20; n₁ =2, n₂ =6, n₃ =9;d₁ =0,36, d₂ =0,4, d₃ = 0,44. Отсюда:

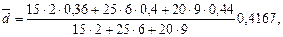или 41,67%

Поскольку уже определена средняя ставка, то для нахождения среднего срока воспользуемся формулой (35):

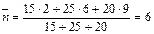месяцев.

Если же, как это обычно делается, время учитывать при определении среднего срока, то по формулам (36) и (33) получим:

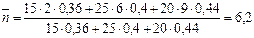месяца;

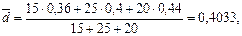или 40,33%

Пример 1.5.5. Банк выдает предпринимателю три ссуды соответственно на 180, 300 и 240 дней под простые ставки 38,45 и 40% годовых. После того как банк при выдаче ссуд взыскал простые обыкновенные проценты, предприниматель получил на руки суммы 30 тыс., 20 тыс. и 50 тыс. руб. Определите средний срок ссуды.

Решение. Поскольку проценты удержаны сразу, то на выданные суммы по существу происходит наращение по соответствующим учетным ставкам. Пусть P₁ = 30 тыс. руб., Р₂ = 20 тыс. руб., P₃ = 50 тыс. руб., d₁ = 0,38, d₂ = =0,45, d₃ = 0,4. Воспользуемся формулой (36). Можно либо в ней заменить F_k на 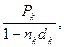либо вначале найти 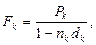а затем применить формулу (36).

Поступим в соответствии с последним способом, т.е. вначале найдем суммы, которые надо вернуть банку. Обратим внимание, что в данном случае при вычислениях исходные сроки необходимо перевести в годы: n₁= =180/360=0,5 года, n₂ = 300/360=0,833 года, n₃ = 240/360 = 0,667 года. Применяя формулу (20), получим:

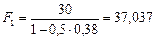тыс. руб.

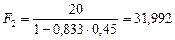тыс. руб.

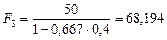тыс. руб.

А теперь воспользуемся формулой (36), причем для упрощения расчетов заметим, что 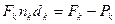. Следовательно,

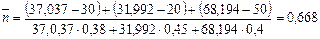года,

т.е. 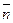= 360 • 0,668 = 240,48 дня. Округляя, получим средний срокссуды, равный 241 дню.

Полезно представлять себе и другой способ решения. Можно вначале определить по формуле (25) эквивалентные простые процентные ставки:

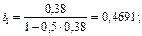
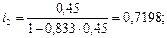
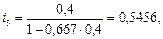
а затем воспользоваться формулой (30):

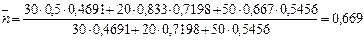года.

Пример 1.5.6. Банк использовал в течение 4 месяцев депозиты на суммы 40,20 и 80 тыс. руб., размещенные соответственно на 1, 2 и 1 месяц по простым процентным ставкам 34, 30 и 42% годовых. Определите стоимость привлеченных средств за 4 месяца для банка в виде средней годовой процентной ставки.

Решение. Полагаем Р₁ = 40 тыс. руб., Р₂ = 20 тыс. руб., Р₃ = 80 тыс. руб.; i₁ = 34%; i₂ = 30%; i₃ = 42% и воспользуемся формулой (29). Так как исходные ставки берем в процентах (а это, как уже отмечалось, благодаря виду формулы можно сделать), то и результат получим в процентах:

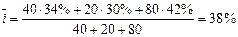
Заметим, что другой способ определения стоимости привлеченных средств основан на использовании формулы (23), где через Р обозначена использованная сумма средств; через F - Р - проценты, выплаченные за использование суммы Р в течение времени п. Таким образом, эта стоимость (обозначим ее через 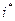) определяется по формуле

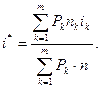
Поскольку для любого k=1,2,…,m справедливо 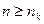, то нетрудно показать, что для 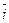из формулы (29) выполнено неравенство 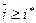. Если 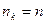, для любого k = 1,2,...,m, то .

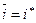В нашем примере n₁=1 месяц, п₂ = 2 месяца, п₃ = 1 месяц, n = 4 месяца, поэтому

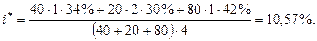
Если бы все депозиты были размещены в течение 4 месяцев, то получили бы i^* = 38%.

В ситуации, когда банк выдает денежные средства, ставк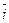и и 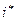определяют доходность для банка выданных средств. Величину 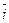называют также средневзвешенной доходностью.

Валютные расчеты

Основные положения

· В процессе взаимного обмена национальных валют устанавливается их курс, представляющий собой цену денежных единиц одной страны, выраженную в денежных единицах другой страны. Само определение курса валют называется их котировкой. Полная котировка предполагает определение курса покупателя (покупки) и курса продавца (продажи), согласно которым банки покупают и продают валюту. Единица низшего разряда установленной котировки называется пунктом.

· Курс валют в зависимости от формы его выражения называется обменным или девизным. Обменный курс показывает, сколько единиц отечественной валюты можно получить в обмен на единицу иностранной, т.е. это цена иностранной валюты, выраженная в единицах отечественной валюты. Девизный курс, являясь обратной величиной к обменному, показывает, сколько единиц иностранной валюты можно получить за единицу отечественной, т.е. это цена отечественной валюты, выраженная в единицах иностранной валюты. Определение обменного курса также называют прямой котировкой, а девизного курса - косвенной котировкой.

· Кроме обменного и девизного используются также и кросс-курсы валют, представляющие собой соотношения между двумя валютами, следующие из их курсов по отношению к некоторой третьей валюте.

· Девизы называются конвертируемыми, если есть возможность их свободного обмена (конверсии) на валюту других стран по действующему курсу.

· Финансовая операция, связанная с инвестированием денежных средств в валюте, в общем виде представляет собой последовательность следующих действий: конвертирование средств в другую валюту; размещение на рынках финансовых инструментов полученных средств на некоторый срок; обратная конвертация средств, полученных от инвестирования, в исходную (или иную) валюту.