Основные сведения из технической механики жидкости

Техническая гидроаэромеханика изучает законы движе­ния, относительного покоя и взаимодействия жидкости с твердыми телами, которые либо находятся в ней, либо ее ограничивают. Под жидкостьюпонимают такую мате­риальную среду, медленная деформация которой при по­стоянном объеме возможна под действием ничтожно ма­лых сил. Жидкости делятся на два класса: малосжимае­мые - капельныеи сжимаемые - газы. При движении газов со скоростями, значительно меньшими скорости звука, сжимаемостью газа можно пренебречь. В этом случае при исследовании движения газов применяют уравнения движения капельных жидкостей.

Техническая механика жидкости базируется на ос­новных законах сохранения массы, энергии и импульса, которые широко применяются в технике.

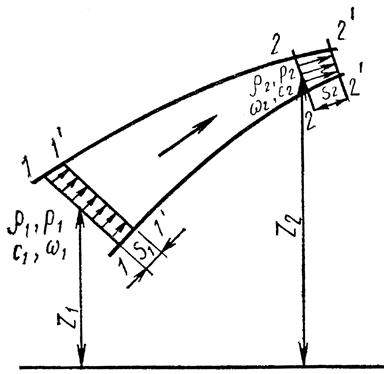
Уравнение неразрывности потока.Рассмотрим уста­новившееся движение жидкости в канале произвольного сечения (рис. 1). Пусть поток движется со скоростью с от сечения 1 - 1к сечению 2 - 2. В соответствии с зако­ном сохранения массы вещества та масса жидкости, ко­торая находится между сечениями 1 - 1 и 2 - 2, для рас­сматриваемого случая движения должна быть постоян­ной. Это означает, что масса жидкости, прошедшая че­рез живое сечение канала площадью будет равна массе жидкости, прошедшей через живое сечение кана­ла площадью , т. е.

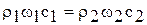, (16)

где 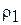и - плотность жидкости, проходящей через сечение 1 - 1и 2 - 2соответственно.

Выражение (16), являясь следствием закона сохра­нения массы, называется уравнением неразрывностипо­тока жидкости. Из уравнения неразрывности потока, часто записываемого в виде:

, (17)

следует, что, если предположить существование внутри установившегося потока жидких струек, для каждой из которых должно выполняться условие (17), то они нигде не могут закончиться. Эти струйки либо должны простираться от одной границы рассматриваемого про­странства до другой, либо замыкаться. В тех случаях, когда несжимаемые (капельные) жидкости или газы движутся под действием относительно малых перепадов давления и весь поток рассматривается как одна жидкая струйка, произведение называют объемным рас­ходом потока, а произведение 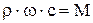- массовым рас­ходом.

Уравнение движения.Известно, что основными си­лами, действующими в движущейся жидкости, являют­ся массовые и поверхностные. Если канал, в котором движется жидкость, является неподвижным, то единст­венной массовой силой, действующей в жидкости, будет вес. К поверхностным силам относятся силы гидродина­мического давления и силы трения.

Рис. 1. Схема потока к вы­воду уравнения сохранения массы

Количественной мерой различных форм движения материи служит понятие, называемое в физике энер­гией. Если тело движется, то оно обладает энергией; если тело обладает энергией, оно может совершить ра­боту, которая в дальнейшем (в соответствии с принци­пами сохранения энергии) может перейти в другую фор­му энергии (например, в тепловую).

Рис. 2. Схема потока к вы­воду уравнения сохранения энергии

Рассмотрим установившееся движение вязкой жидко­сти с учетом ее сжимаемости. Как известно, при движе­нии сжимаемых жидкостей работа сил трения оказыва­ет двоякое действие: с одной стороны, являясь реактив­ной силой, она тормозит поток, действуя в противопо­ложном движению направлении; с другой стороны, рабо­та сил трения, целиком превращаясь в теплоту, возвра­щается в поток в виде тепловой энергии, которая может расходоваться на расширение жидкости и, следователь­но, на ускорение ее движения.

Выделим некоторый объем в трубке тока движущей­ся жидкости и ограничим его сечениями 1-1 и 2-2(рис. 2). Рассматривая установившееся движение, за­пишем для этого объема уравнение сохранения энергии в следующей формулировке: работа внешних сил плюс подведенная теплота расходуются на изменение механи­ческой и внутренней энергии рабочего тела. Как извест­но, внешними силами, действующими при перемещении жидкости от сечения 1-1к сечению 2-2, являются силы давления и силы трения. Пусть за некоторый про­межуток времени tпод действием сил давления произо­шло перемещение объема жидкости, заключенного меж­ду сечениями 1-1 и 2-2,в сечения 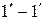и . Это означает, что вблизи сечения 1-1( рис. 2) исчез­нет элемент массы

,

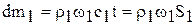а около сечения 2-2появится равный ему элемент массы

.

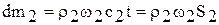Работа сил давления, действующих на площадь сече­ния 1-1, равна ,а на площадь сечения 2-2 - .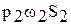

Спроектируем все силы на направление движения массы жидкости. Силы гидродинамического давления, действующие на боковую поверхность выделенного объе­ма, составляющих в направлении движения не дадут, и их работа по перемещению массы жидкости равна нулю. Таким образом, суммарная работа сил давления, под действием которых произошло перемещение жидкости из сечения 1-1 в сечение 2-2, определится выражением:

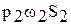- = , (18)

где , 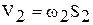– объем жидкости, прошедший соответственно через сечение 1-1 и 2-2 за время t.

Разделив каждый из объемов 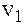и на массу жидкости, находящейся в этом объеме, вместо выражения (18) получим выражение для удельной работы сил давления

,

где 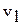и 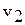-удельный объем жидкости, прошедшей через сечения 1-1и 2-2соответственно.

Обозначим удельную работу сил трения, возникающую в потоке движущейся жидкости при перемещении ее из сечения 1-1 в сечение 2-2,DR. Таким образом, суммарная удельная работа внешних сил,совершаемая при перемещении потока жидкости из сечения 1-1 в сечение 2-2, с учетом направления действия этих сил запишется в виде .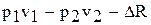

Вследствие работы вязких сил возможный приток теплоты в трубку тока между сечениями 1-1 и 2-2будет равен МDq, где Dq - количество теплоты, полу­ченное каждой единицей массы жидкости, прошедшей путь между этими сечениями. Таким образом, Dq - удельное количество теплоты, поступающей в массу жидкости между сечениями 1-1 и 2-2.

В соответствии с законом сохранения энергии удельная работа внешних сил и подведенная теплота должны привести к изменению удельных механической и внутренней энергий потока жидкости. Удельную внутреннюю энергию массы жидкости обозначим через U. Тогда, если принять, что потенциальная энергия обусловливается только полем сил тяжести (gZ), содержание энергии в массе элемента жидкости dm,прошедшей через сечение 1-1, будет равно:

,

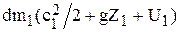а через сечение 2-2

,

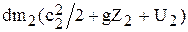где 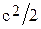- удельная кинетическая энергия элемента массы.

Масса жидкости, находящейся между сечениями 1-1 и 2-2, остается постоянной, поэтому изменение удельной энергии при перемещении жидкости из сечения 1-1 в сечение 2-2определится как разность удельных энер­гий элементов массы 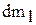и . Таким образом, закон сохранения удельной энергии для выделенного элемен­та трубки тока может быть записан в виде

. (19)

Полученное выражение (1.4) часто используется в дифференциальной форме:

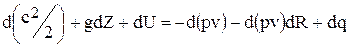. (20)

Уравнение сохранения энергии (20) может быть до­полнено уравнением, вытекающим из первого начала термодинамики, согласно которому подведенная к си­стеме теплота увеличивает ее внутреннюю энергию и со­вершает работу расширения, т. е.

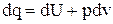. (21)

Подставляя выражение (21) в уравнение (20) и имея в виду

получаем:

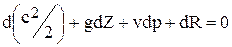. (22)

После интегрирования имеем выражение:

, (23)

представляющее собой уравнение Д. Бернулли, учиты­вающее как сжимаемость жидкости, так и работу сил трения. Каждый член уравнения (23) определяет удель­ную энергию или удельную работу. Рассмотрим несколь­ко частных случаев записи этого уравнения.

1. Жидкость реальная, несжимаемая. Для несжимаемой жидкости имеем

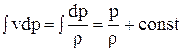
и уравнение (23) можно записать в виде:

,

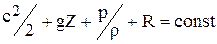где R-потеря удельной энергии.

Рассматривая гидравлику капельных жидкостей, уравнение Д. Бернулли удобно записывать в виде сум­мы напоров. Для этого энергию и работу относят к весу жидкости.

Для записи уравнения (23) в виде напоров каждый член этого уравнения надо разделить на величину g, тогда получим:

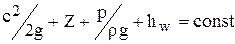, (24)

где 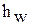- потери напора.

2. Жидкость идеальная, несжимаемая. Как известно, в случае движения идеальной жидкости удельная работа сил трения (или потери) равна нулю и уравнение (24) приобретает вид:

.

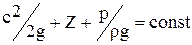3. Жидкость идеальная, сжимаемая. В этом случае R = 0, а интегрирование выражения 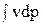зави­сит от функциональной связи между удельным объемом v и давлением p. Эта связь определяется только тер­модинамическим процессом. Так, при изотермическом течении жидкости можно воспользоваться уравнением состояния, согласно которому

.

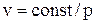При адиабатическом течении жидкости эта связь определяется из уравнения адиабаты:

,

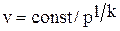где 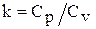-показатель адиабаты (здесь С_р и С_v - удельная теплоемкость соответственно при постоянном давлении и объеме).

В этом случае уравнение Д. Бернулли имеет вид:

для изотермического течения

,

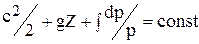для адиабатического течения

.

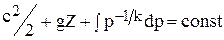В тех случаях, когда течение газа происходит под действием относительно малого перепада давлений, его сжимаемость в процессе движения можно не учитывать. В этом случае уравнение Д. Бернулли (23) принято записывать в виде уравнения для единицы объема пе­ремещаемой жидкости:

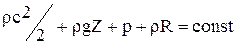. (25)

Имея в виду, что член rdZсущественно мал по срав­нению со всеми другими слагаемыми выражения (25), а 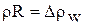, уравнение (25) можно представить в сле­дующем виде:

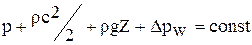. (26)

Уравнение Д. Бернулли имеет различные формы записи для решения многих практических задач.

Гидравлические сопротивления.Для расчета водо­проводных сетей уравнение Д. Бернулли часто исполь­зуется в виде выражения (24), а для расчета вентиля­ционных сетей - в виде выражения (26). Каждое из этих уравнений содержит в качестве слагаемого член, учитывающий работу сил трения в потоке и называе­мый «потерей напора» 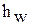или «потерей давления» .

На практике встречаются два вида гидравлических потерь: потери по длине и местные потери. Потери по длине наблюдаются в каналах постоянного сечения и увеличиваются пропорционально длине канала. Они зависят как от состояния внутренней поверхности стенок канала, так и от режима движения жидкости. В качест­ве геометрической характеристики, определяющей со­стояние поверхности стенок канала, принята относитель­ная эквивалентная шероховатость 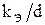. Режим движе­ния жидкости определяется числом Рейнольдса 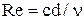, где с-характерная скорость движения потока жидкости, d-характерный размер потока, n - кинема­тическая вязкость жидкости.

Потери на участке длиной 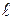вычисляются по форму­ле Дарси-Вейсбаха, Для определения потерь напора она используется в виде:

,

потерь давления

.

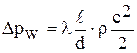Если потери по длине возрастают пропорционально длине канала, то потери в местных сопротивлениях от длины не зависят. Эти потери возникают всегда, когда имеется деформация потока. Под деформацией понима­ют сужение и последующее расширение потока, вызванные либо изменением направления движения (поворот сети), либо установкой в сети трубопроводной арматуры (краны, вентили, задвижки, шиберы, дроссели, шайбы, муфты и т. д.).

Потери напора (или давления) в местных сопротив­лениях также тесно связаны с работой сил трения. Для понимания механизма потерь, возникающих при турбу­лентном движении в местных сопротивлениях, рассмот­рим явление, называемое внезапным расширением по­тока. Пусть поток, вытекая из трубы диаметром ,по­падает в трубу большего диаметра 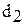(рис. 3). Дви­гаясь в продольном направлении со скоростью c,части­цы жидкости массой m обладают количеством движе­ния 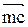. Вследствие поперечных пульсаций скорости эти частицы попадают в область, находящуюся вне преде­лов струи, вытекающей из узкого сечения. В результате проявления вязкости часть количества движения такой жидкой частицы передается тем частицам, которые на­ходятся вне узкой части струи. Эти жидкие частицы, получив некоторую часть количества движения, начи­нают перемещаться в продольном направлении, расши­ряя тем самым зону жидкости, находящуюся в движе­нии. Так, в результате поперечных пульсаций при пере­даче количества движения от одной частицы к другой происходит постепенное расширение потока. Увеличение площади сечения

Рис. 3. Схема движения потока в местном сопротивлении

расширяющейся струи происходит вместе с увеличением расхода потока жидкости вдоль нее. Поскольку должно выполняться условие неразрыв­ности потока, то расход жидкости, вытекающей из сече­ния 1-1, должен быть равен ее расходу, вытекающему из сечения 2-2. Следовательно, та часть жидкости, ко­торая была вовлечена в движение вязкими силами, должна вернуться. Таким образом, в расширяющейся части потока возникает постоянно вращающаяся масса жидкости (валец). Энергия, расходуемая потоком на поддержание движения в вальце за счет работы вязких сил, и является потерей напора в местном сопротивле­нии. 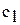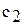Если и - скорости потока соответственно в се­чениях 1-1 и 2-2,то потери определяют по формуле Борда - Карно:

; .

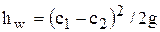Таким образом, в любом местном сопротивлении всег­да имеются сужение потока, а затем его расширение. К сожалению, до настоящего времени не существует ме­тодов теоретического определения площади сечения струи при сужении потока в трубопроводной арматуре. Поэтому потери в местных сопротивлениях принято оп­ределять по формулам:

; .

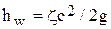Коэффициент местного сопротивления z зависит от соотношения площадей узкого и широкого се­чений:

,

поэтому он определяется экспериментально.

Таким образом, если иметь в виду, что гидравличе­ская сеть состоит из n линейных, последовательно рас­положенных участков различных длины и диаметров, и в этой сети имеются mразличных местных сопротив­лений, то суммарные потери в сети определяются по формуле:

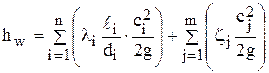
или

.

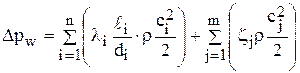Уравнение сохранения импульса.Теорема о сохране­нии импульса, хорошо известная из общей механики, очень часто применяется в задачах, связанных с уста­новившимся движением жидкости. Согласно этой тео­реме изменение количества движения массы жидкости в единицу времени равно сумме всех внешних сил, дей­ствующих на эту массу. Особенность применения этой теоремы для массы жидкости состоит в том, что для ее применения требуются данные о состоянии потока только на границе выделенного объема жидкости. Это позволяет получить сведения о таких гидродинамических явлениях, детали которых внутри рассматриваемого объема учтены быть не могут. Действительно, при уста­новившемся движении на место каждой ушедшей части­цы внутри выделенной массы придет другая, обладаю­щая теми же свойствами (плотностью, скоростью и т. д.). Поэтому для определения количества движения доста­точно знать только то, что происходит на границах вы­деленной массы жидкости. Рассмотрим поток жидкости, изображенный на рис. 1. Изолируем массу жидкости, находящуюся между сечениями 1-1и 2-2. В единицу времени переносится количество движения: через контрольную поверхность 1-1

,

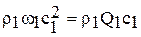через контрольную поверхность 2-2

.

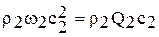Изменение количества движения равно:

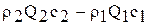. (27)

В сечениях 1-1и 2-2из внешних сил действуют только силы гидродинамического давления, поэтому равнодействующая всех сил будет равна:

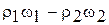. (28)

Воспользовавшись формулировкой закона сохране­ния импульса и выражениями (27) и (28), получим для течения жидкости в канале уравнение сохранения импульса в виде:

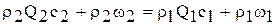
или

. (29)

Полученное уравнение сохранения импульса (29) совместно с уравнением Д. Бернулли (23) и уравнением неразрывности (17) составляют основу при решении многих инженерных задач технической механики жид­кости.

Циркуляция скорости.Изучение работы лопастных нагнетателей тесно связано с использованием такого по­нятия, как циркуляция скорости. Назовем криволинейным интегралом скорости вдоль кривой АВ интеграл от скалярного произведения вектора скорости с на линей­ный элемент длины 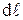кривой АВ,т.е.

.

Если a есть угол между векторами с и 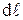, то

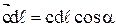
Рис. 4. К вычислению циркуляции скорости по замкнутому кругу

Криволинейный интеграл скорости, взятый вдоль замкнутого контура L(рис. 4), называется циркуля­цией скоростии обозначается буквой Г. Применяя для интеграла вдоль замкнутого контура знак можно записать:

(30)

При решении ряда задач гидродинамики пользуются теоремой Томсона: в потенциальном однородном пото­ке жидкости циркуляция скорости по любому замкнутому контуру во время движения жидкости остается постоянной.

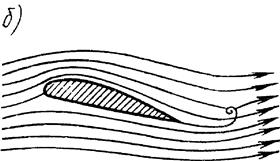
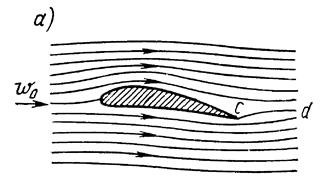
в)	Рис. 5. Схема движения потока при обтекании профиля: а - поверхность раздела при потенциальном потоке; б - вихрь, образовавшийся из поверхности раздела, в - циркуляционный по­ток вокруг профиля

Из этой теоремы можно получить множество различных следствий. Если, например, движение жидкости начинается из состояния покоя, т. е. в начальный момент, а циркуляция скорости вдоль каждой замкнутой жидкой линии заведомо равна нулю, то и в дальнейшем она остается равной нулю. Это означает, что потенци­альный поток не может стать вихревым.

Однако существуют потенциальные течения, в кото­рых циркуляция скорости в целом для всего потока не равна нулю. Необходимым для этого условия яв­ляется многосвязностьобласти, в которой происходит течение. Под многосвязной понимают такую область или плоскость, где замкнутые кривые нельзя стянуть в точку, не разрывая этих кривых. Область становится многосвязной, когда, например, поток жидкости обте­кает какое-либо препятствие - цилиндр или другое тело. В этом случае за телом образуется вихрь, который сры­вается и уносится потоком, оставляя вокруг профиля циркуляцию скорости, равную по величине и противо­положную по направлению (в соответствии с теоремой Томсона).

Рассмотрим механизм возникновения циркуляции скорости при обтекании потенциальным потоком жидко­сти аэродинамического профиля (рис. 5). При асим­метричном обтекании профиля в кормовой части встре­чаются два потока, имеющие различные скорости обте­кания. Поверхность, которая условно делит эти два по­тока, называется поверхностью раздела (на рис. 5, а линия cd). Вследствие неустойчивости поверхность раз­дела распадается, сворачиваясь в вихрь (рис. 5,б). Так как поток потенциальный, то сумма вихрей, обра­зующаяся в потоке, должна обеспечить в нем нулевую циркуляцию скорости по любому замкнутому контуру, не охватывающему обтекаемое тело. Поэтому оторвав­шийся от профиля вихрь вызывает вокруг него циркуля­цию скорости, равную по абсолютному значению своей циркуляции, но противоположно направленную. С цир­куляцией тесно связано возникновение подъемной силы.

Рис. 6. Схема обтекания по­тока вязкой жидкости вра­щающегося цилиндра

Как видно из рис. 5, в, при сложении циркуляционно­го и потенциального потоков скорость последнего над профилем увеличивается, а под профилем - уменьшает­ся. В соответствии с уравнением Д. Бернулли давление под профилем возрастет и, следовательно, возникнет суммарная сила давления, действующая в направлении верхней кромки профиля.

Циркуляция скорости может возникнуть при обтека­нии тела как потенциальным, так и вязким потоком жидкости. Для иллюстрации рассмотрим поперечное об­текание потоком вязкой жидкости цилиндра, вращающе­гося с постоянной скоростью (рис. 6). Как известно, вблизи поверхности твердого тела в жидкости возни­кает тонкий пограничный слой. Поскольку вязкие силы в этом слое существенны, очевидно, что те частицы жидкости, которые находятся вблизи вращающегося ци­линдра, приобретут движение в направлении вращения цилиндра. Циркуляция скорости, причиной возникнове­ния которой является трение, создает силу, действую­щую на цилиндр в направлении, перпендикулярном на­правлению потока. Поэтому эта сила называется по­перечной. Поперечная сила всегда направлена от той стороны вращающегося тела, на которой направление вращения и направление потока противоположны к той стороне, на которой эти направления совпадают. Воз­никновение при указанных условиях поперечной силы называется эффектом Магнуса(по имени ученого, впер­вые открывшего это явление в 1852 г.).

Циркуляцию скорости можно определить, если рас­смотреть в качестве примера простейший случай, когда жидкость вращается как твердое тело с угловой ско­ростью вокруг некоторой оси. Возьмем в плоскости, перпендикулярной оси вращения, площадку, ограничен­ную окружностью радиусом r с центром на оси враще­ния и вычислим циркуляцию скорости вдоль этой окруж­ности. Так как окружная скорость течения жидкости в точках окружности равна 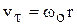и направлена по касательной к окружности, то циркуляция скорости вдоль выбранного контура (окружности) равна:

.

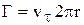Подставляя в полученное выражение значение окруж­ной скорости, имеем

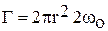. (31)

Таким образом, циркуляция скорости по замкнутому контуру равна площади контура, умноженной на удво­енную угловую скорость вращения жидкости. В курсах гидромеханики показано, что циркуляцию скорости мож­но вычислить подобным образом для любого замкну­того контура, проведенного в массе жидкости.