Математические методы описания линейных стационарных непрерывных систем
3.1.Общая характеристика методов
Всякая система, рассматриваемая с точки зрения зависимости выходных и входных величин как функций времени, носит название динамической системы. Система слежения и ее отдельные звенья относятся к динамическим системам. Для исследования динамических систем используются временные и частотные методы.
Временные методы используют дифференциальные уравнения и полученные с их помощью передаточные функции, переходные и весовые функции.
Частотные – используют частотные передаточные функции и логарифмические частотные характеристики.
Временные методы используются при исследовании линейных нестационарных систем. Для стационарных систем предпочтительно применение частотных методов.
Задачей исследования системы является определение реакции системы на входное воздействие, либо определение параметров систем.
3.2.Использование дифференциальных уравнений
Для составления дифференциального уравнения (ДУ), связывающего входные и выходные величины в системе, составляют дифференциальные (или алгебраические) уравнения, для всех звеньев, входящих в систему, на основе физики происходящих в них процессов. Число таких дифференциальных уравнений равно числу звеньев системы. Затем, оставляя входную и выходную величины в качестве основных, избавляются от промежуточных величин, производя последовательную подстановку одного уравнения во второе. Для упрощения процесса подстановки уравнения записывают в сокращенной форме.
В общем виде ДУ можно записать следующим образом:
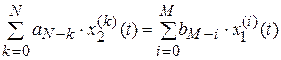 , при
, при 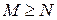 (3.1)
(3.1)
x2(t), x1(t) – выходные и входные величины соответственно; a,b – коэффициенты.
ДУ может быть записано в сокращенной форме.
Введем обозначение 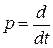 .
.
Теперь мы можем формально вынести за знак суммы значения x2(t) и x1(t).
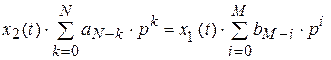
или
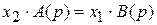 (3.2)
(3.2)
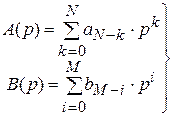 дифференциальные полиномы.
дифференциальные полиномы.
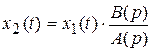 ,
,
или же можно записать в сокращенной форме:
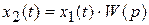 ,
,
где 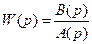 ─ операторный коэффициент передачи.
─ операторный коэффициент передачи.
Приведенную форму записи определяют как алгебраизированную (символическую).
Общее решение ДУ определяет изменение во времени управляемой величины при заданном входном воздействии, и позволяет, таким образом, полностью описать процессы в следящей системе. Общее решение ДУ является суммой общего решения однородного ДУ, получаемого из уравнения (1) приравниванием нулю его правой части, и частного решения неоднородного ДУ.
Однородное ДУ определяет характер собственных колебаний в системе. Его решение позволяет исследовать систему на устойчивость.
Неоднородное ДУ определяет реакцию системы на внешние воздействия. Его решение позволяет оценить точность воспроизведения задающего воздействия.
3.3.Использование передаточных функций
Для получения алгебраической формы записи надо перейти в область изображений по Лапласу.
Пусть система описывается уравнением (3.1) .
Применим преобразование Лапласа к обеим частям уравнения (3.1), учитывая, что:
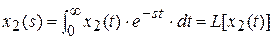 ,
,
где 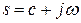 ─ переменная Лапласа;
─ переменная Лапласа;
и 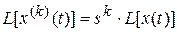 при нулевых начальных условиях (*
при нулевых начальных условиях (* 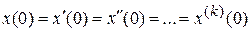 .
.
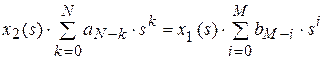 ,
,
отсюда найдем х2
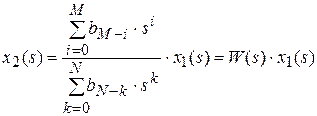 ,
,
где W(s) – передаточная функция ─ реакция системы на входное воздействие в области изображений Лапласа.
Таким образом, передаточная функция W(s) определяется как отношение изображений по Лапласу выходной и входной величин при нулевых начальных условиях.
В последующем изложении W(s) и W(p) мы будем именовать передаточной функцией, имея в виду, что s- комплексная переменная, а p- оператор дифференцирования.
В данном случае мы получили алгебраическую форму записи ДУ. Формально она может быть получена из упрощенной символической формы заменой оператора дифференцирования на переменную s и оригиналов на изображения:
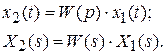
Для нахождения оригинала может быть использовано обратное преобразование Лапласа:
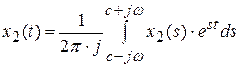 .
.
Обратное преобразование выполняют путем разложения изображения на простейшие дроби и последующего использования таблиц.
3.4. Использование переходной и весовой функций
Переходной функцией называют реакцию системы на ступенчатую единичную функцию, которую определяют как 1(t) (рис. 3.1):
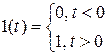 .
.
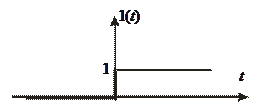
Рис. 3.1. Единичная ступенчатая функция
Переходная функция используется при исследовании переходных режимов следящих систем. Переходная характеристика – графическое изображение переходной функции. Типовые переходные характеристики следящих систем изображены на рис. 3.2.
Устойчивые системы

Неустойчивые системы
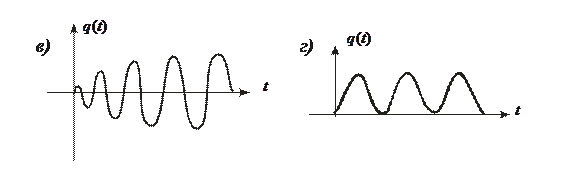
Рис. 3.2. Переходные характеристики
Переходная характеристика может быть найдена аналитически. Запишем реакцию системы на 1(t) в виде ДУ в сокращенной форме:
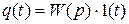 ,
,
где W(p) – операторный коэффициент передачи.
Перейдя в область изображений по Лапласу, получим следующие выражения:
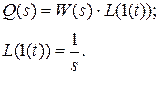
Осуществив обратное преобразование Лапласа, получим переходную функцию q(t).
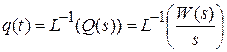 .
.
Весовая функция (импульсная характеристика) – реакция системы на воздействие в виде δ-функции, определяемой как
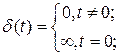
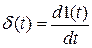 .
.
Отметим некоторые свойства δ-функции:
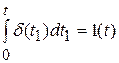 ;
;
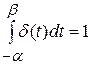 .
.
Весовая функция h(t) равна:
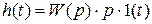 .
.
Переходя в область изображений, получим следующие выражения:
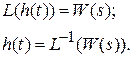
Таким образом, весовая и передаточная функции связаны преобразованием Лапласа.
Весовая функция используется для определения выходной величины с помощью интеграла Дюамеля:
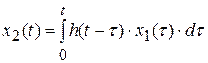 . (3.3)
. (3.3)
В соответствии с условием физической реализуемости: реакция системы на входное воздействие появляется не раньше воздействия, т. е
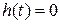 , при t<0,
, при t<0,
можно записать:
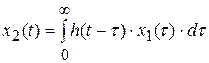 . (3.4)
. (3.4)
Для определения установившегося значения можно полагать, что воздействие началось в момент 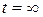 и для расчета использовать выражение:
и для расчета использовать выражение:
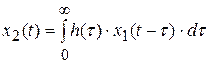 .
.
3.5. Использование частотных передаточных функций
Частотная передаточная функция (комплексный коэффициент передачи) определяет реакцию системы на гармоническое входное воздействие и используется для анализа следящих систем. Ее можно найти, используя ДУ (3.1), если полагать, что 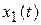 – гармоническое воздействие в комплексной форме определяется выражением
– гармоническое воздействие в комплексной форме определяется выражением
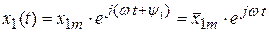 , (3.5)
, (3.5)
где 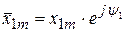 - комплексная амплитуда.
- комплексная амплитуда.
Будем искать частное решение неоднородного ДУ (1) в виде:
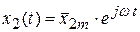 , (3.6)
, (3.6)
где 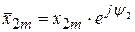 .
.
Подставляя (3.5), (3.6) в (3.1) и учитывая, что
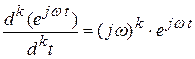 ,
,
получим:
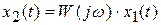 ,
,
где 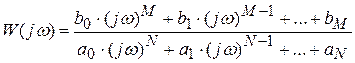 ─ частотная передаточная функция (комплексный коэффициент передачи).
─ частотная передаточная функция (комплексный коэффициент передачи).
Частная передаточная функция – это отношение комплексных амплитуд входных и выходных гармонических воздействий при нулевых начальных условиях.
W(jω) можно получить формально из W(s), заменой s на jω.
W(jω)можно представить а показательной и алгебраической форме:
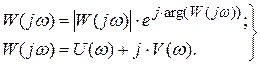
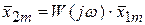
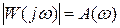 - модуль частотной передаточной функции.
- модуль частотной передаточной функции.
W(jω) на комплексной плоскости изображается в виде вектора. При изменении частоты в интервале ( 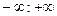 ) конец вектора прочерчивает кривую, называемую амплитудно-фазовой характеристикой (АФХ) (рис. 3.3).
) конец вектора прочерчивает кривую, называемую амплитудно-фазовой характеристикой (АФХ) (рис. 3.3).
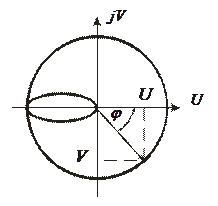
Рис. 3.3. Амплитудно-фазовая характеристика
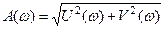 – амплитудно-частотная характеристика (АЧХ).
– амплитудно-частотная характеристика (АЧХ).
АЧХ – зависимость амплитуды выходного сигнала от частоты при неизменной амплитуде входного сигнала.
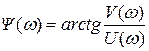 ─ фазочастотная характеристика (ФЧХ).
─ фазочастотная характеристика (ФЧХ).
ФЧХ определяет зависимость фазового сдвига выходного сигнала относительно входного от частоты. Она симметрично относительно начала координат.
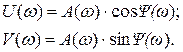
Годограф – кривая, прочерчиваемая концом вектора, при изменении частоты ω в интервале ( 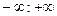 ).
).
3.6. Использование логарифмических частотных характеристик
Метод логарифмических частотных характеристик (ЛЧХ) используется как для анализа, так и для синтеза следящих систем. Метод построения ЛЧХ состоит в графическом изображении АЧХ и ФЧХ в логарифмическом масштабе. Особенно удобен метод, использующий асимптотические логарифмические амплитудно-частотные характеристики ( ЛАЧХ). Для некоторых систем, называемых мимнимально-фазовыми, достаточно построить лишь ЛАЧХ, так как она определяет все свойства системы. К минимально-фазовым относят системы, у которых корни характеристических уравнений, составленных из числителя и знаменателя передаточной функции имеют отрицательные вещественные части.
Метод построения асимптотических ЛАХ состоит в следующем. Выражение для ЛАЧХ и ЛФЧХ записываются в виде
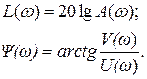
Частота откладывается по оси абсцисс в логарифмическом масштабе, а усиление – в децибелах (дБ) по оси ординат. Логарифмическая фазочастотная характеристика (ЛФЧХ) строится под ЛАЧХ с общей осью частот.
Метод построения асимптотических ЛАХ рассмотрим на примере.
Пусть передаточная функция разомкнутой системы определяется выражением
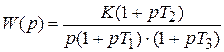 .
.
Заменой переменной перейдем к частотной передаточной функции
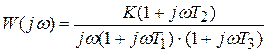 ,
,
где Т1, Т2, Т3 – постоянные времени соответствующих звеньев; К – коэффи циент усиления или добротность (имеет размерность частоты).
Модуль частотной передаточной функции А(ω) последовательно включенных звеньев определяется как произведение модулей этих звеньев. а аргумент – как сумма фазовых сдвигов звеньев.
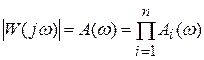 ;
;
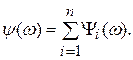
Обычно полагают, что 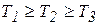 . Пусть Т1 > Т2, > Т3.
. Пусть Т1 > Т2, > Т3.
Обозначим 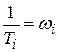 – сопрягающая частота;
– сопрягающая частота; 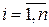 . Тогда
. Тогда
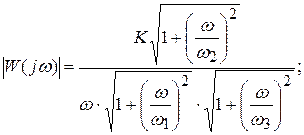
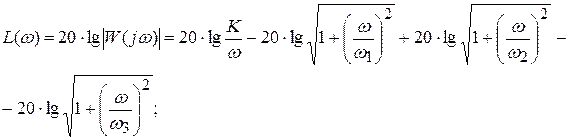
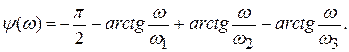 ;
;
При построении асимптотических ЛАХ используется следующее правило:
Если 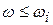 , то пренебрегают вторым слагаемым, т.е.
, то пренебрегают вторым слагаемым, т.е. 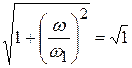 .
.
Если 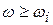 , то пренебрегают единицей,
, то пренебрегают единицей, 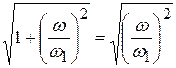
При этом в точке сопряжения ошибка не превышает нескольких дБ.
Асимптотическая ЛАХ для n последовательно включенных звеньев состоит из n+1 асимптоты, каждая из которых строится в диапазоне частот:
1ая: 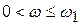 ;
;
2ая: 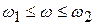 ;
;
… … … … …
n+1: 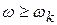 .
.
Построим L(ω) (рис. 3.4).
Уравнение для первой асимптоты ( 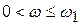 ):
):
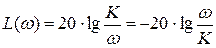 ,
,
при ω = K, L(ω) = 0.
Наклон асимптоты будет равен –20 дБ на декаду.
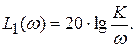
Вторая асимптота строится в диапазоне частот ( 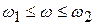 )
)
в соответствии с уравнением:
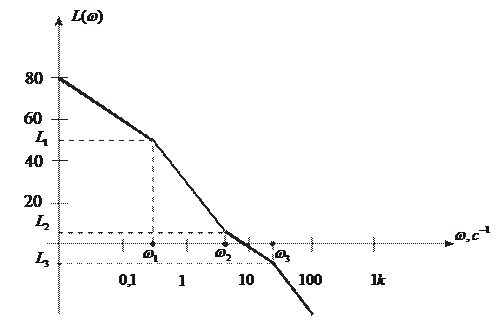
Рис. 3.4. Логарифмическая амплитудно-частотная характеристика
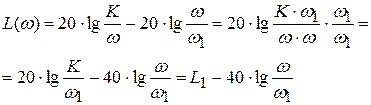 .
.
Наклон асимптоты будет равен –40 дБ на декаду.
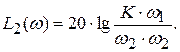
Третья асимптота строится в диапазоне частот ( 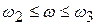 ). Уравнение третьей асимптоты:
). Уравнение третьей асимптоты:
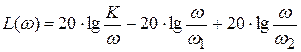
Это уравнение прямой, проходящей через точки L (ω2) и L (ω3),
где 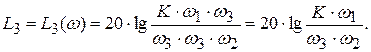 .
.
Таким образом, можно записать:
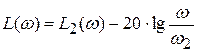
В точке L2 асимптота изменяет свой наклон на +20 дБ, итоговый наклон третьей асимптоты составляет –20 дБ.
Четвертая асимптота строится в диапазоне частот ( 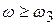 ) в соответствии с уравнением:
) в соответствии с уравнением:
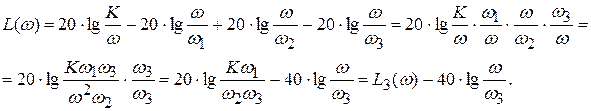
Таким образом, при переходе через сопрягающую частоту ω3 асимптота меняет свой наклон на –20 дБ, и в итоге имеет наклон –40 дБ/дек.
Выводы:
1.При переходе текущего значения частоты через очередную сопрягающую частоту наклон асимптоты изменяется на +20 дБ, если множитель 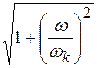 находится в числителе выражения для расчета АЧХ и изменяется на –20 дБ, если этот множитель находиться в знаменателе.
находится в числителе выражения для расчета АЧХ и изменяется на –20 дБ, если этот множитель находиться в знаменателе.
2. Наклон каждой асимптоты кратен 20 дБ /дек.
По ЛАЧХ можно восстановить частотную передаточную функцию.
3.7. Передаточные функции следящих систем
Из изложенного выше следует, что любая из передаточных функций: операторный коэффициент передачи W(p), передаточная функция W(s) и частотная передаточная функция (комплексный коэффициент передачи) W(jw) может быть получена путем замены переменных в известном выражении для одной из вышеназванных передаточных функций.
Определим передаточные функции, связывающие входные и выходные переменные в замкнутой следящей системе, представленной математической моделью (рис. 3.5).
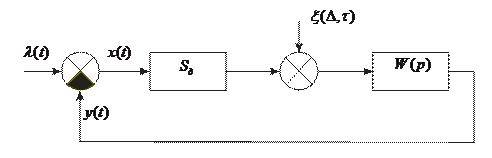
Рис. 3.5. Структурная схема следящей системы
Исходные соотношения:
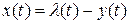 – ошибка слежения. (3.7)
– ошибка слежения. (3.7)
В свою очередь
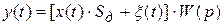 (3.8)
(3.8)
Подставим (3.8) в (3.7) и сгруппируем слагаемые. В результате получим
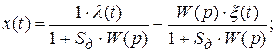
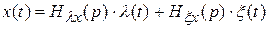 ,
,
где 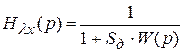 и
и 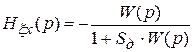 ─ соответственно передаточные функции от воздействия к ошибке и от возмущения к ошибке.
─ соответственно передаточные функции от воздействия к ошибке и от возмущения к ошибке.
Найдены, таким образом, передаточные функции, связывающие ошибку слежения с входным воздействием и с флюктуационной составляющей.
Теперь подставим (3.7) в (3.8) и сгруппируем слагаемые
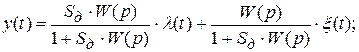
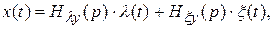
где 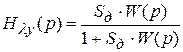 и
и 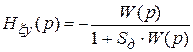 .
.
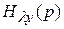 и
и 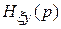 – передаточные функции от воздействия к управляемой величине (связывающие входную и выходную величины) и от возмущения к управляемой величине.
– передаточные функции от воздействия к управляемой величине (связывающие входную и выходную величины) и от возмущения к управляемой величине.
Можно значительно упростить процесс определения передаточной функции, если использовать следующую формулу:
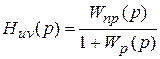 ,
,
где u – входное воздействие, а v – выходная величина;
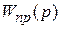 – передаточная функция прямой цепи, связывающей входное воздействие и выходную величину.
– передаточная функция прямой цепи, связывающей входное воздействие и выходную величину.
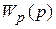 – передаточная функция разомкнутой системы (размыкается в точке подачи обратной связи и определяется как передаточная функция от ошибки x(t) к управляемой величине y(t) .
– передаточная функция разомкнутой системы (размыкается в точке подачи обратной связи и определяется как передаточная функция от ошибки x(t) к управляемой величине y(t) .
3.8. Передаточные функции в обобщенной структурной схеме радиотехнической следящей системы
Основная передаточная функция – передаточная функция замкнутой системы. Определяется отношением изображений по Лапласу управляемой величины и задающего воздействия:
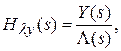
где 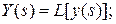
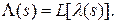
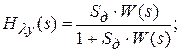
Передаточная функция разомкнутой системы – отношение изображений по Лапласу управляемой величины и ошибки слежения.
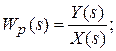
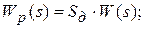
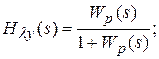
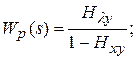
Передаточная функция от воздействия к ошибке – отношение изображений ошибки и задающего воздействия:
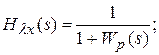
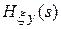 – передаточная функция от возмущения к управляемой величине:
– передаточная функция от возмущения к управляемой величине:
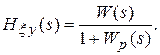
3.9. Типовые динамические звенья следящих систем
Для упрощения анализа следящих систем сложные динамические звенья, описываемые дифференциальным уравнениями высоких порядков, разбивают на ряд простых таким образом, чтобы дифференциальные уравнения, описывающие их работу, были не выше второго порядка:
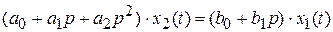 .
.
Этому уравнению соответствует передаточная функция
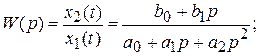
Всё множество динамических звеньев, независимо от назначения, конструктивных особенностей, элементной базы классифицируется по виду дифференциального уравнения, описывающего работу звена или его передаточной функции. По этому признаку классификации различают следующие типы динамических звеньев:
- позиционные;
- интегрирующие;
- дифференцирующие.
К позиционным звеньям относятся: безынерционное, апериодическое звено 1-ого порядка, апериодическое звено 2-ого порядка, колебательное звено.
К дифференцирующим звеньям относятся: идеальное дифференцирующее, инерционное дифференцирующее, форсирующее.
К интегрирующим звеньям относятся: идеальное интегрирующее, инерционное интегрирующее, изодромное.
Апериодическое звено 1ого порядка описывается ДУ следующего вида:
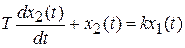 или
или 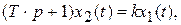
где 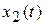 – выходная величина;
– выходная величина; 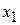 (t) – входная величина; Т─ постоянная времени звена; k─ коэффициент передачи.
(t) – входная величина; Т─ постоянная времени звена; k─ коэффициент передачи.
Передаточная функция
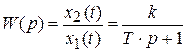 ;
;
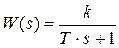 ,
,
где 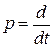 ;
; 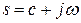 .
.
К этим звеньям относятся исполнительные двигатели, усилители мощности, магнитные усилители , RC – фильтры.
АЧХ звена определяется выражением:
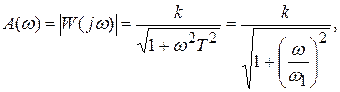
где 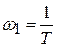 – сопрягающая частота.
– сопрягающая частота.
ФЧХ звена: 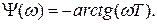
Переходная характеристика:
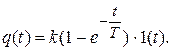
Весовая функция
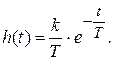
Графическое изображение переходной и весовой функции (рис. 3.6):

Рис. 3.6. Переходная и весовая характеристики апериодического звена
Логарифмическая амплитудно - частотная характеристика
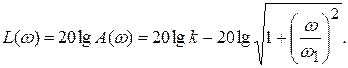
Длительность переходного процесса tп = 3T; q(tп) = 0,95q.
Полоса пропускания 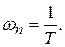
При уменьшении постоянной времени Т увеличивается ωп, и при Т = 0 переходная характеристика будет повторять входной процесс,и в результате получим звено, описываемое уравнением
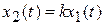 ;
;
такое звено называется безынерционным 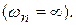 ;
;
Передаточная функция, АЧХ и ФЧХ звена соответственно равны:
W(s) = k; A(ω) = k;Ψ(ω) = 0.
К безынерционным звеньям обычно относят звенья, ширина спектра сигналов, на входах которых значительно уже полосы пропускания.
Рассмотрим пример RC – цепи (рис.3.7)
Такая цепь относится к апериодическому звену и имеет передаточную функцию
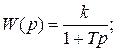
где T =R1R2C/R1+R2.
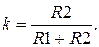

Рис.3.7. Пример апериодического звена
При 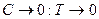 и апериодическое звено трансформируется в безынерционное звено.
и апериодическое звено трансформируется в безынерционное звено.
К колебательным звеньям относят звенья, описываемые дифференциальным уравнением следующего вида:
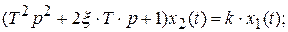
где ξ – коэффициент затухания (для звеньев автоматических систем ξ = 0,5…0.7).
К таким звеньям относятся RLC контура, акселерометры и др.
Обозначим 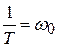 (собственная частота) и разделим почленно все слагаемы числителя и знаменателя на Т2; в результате получим:
(собственная частота) и разделим почленно все слагаемы числителя и знаменателя на Т2; в результате получим:
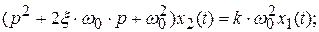
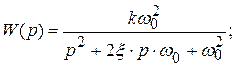
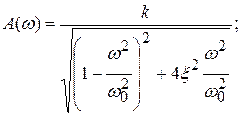
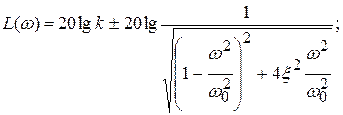
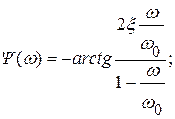
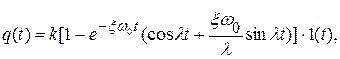
где 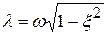 – частота затухающих колебаний;
– частота затухающих колебаний;
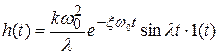 .
.

Рис. 3.8. Переходная и логарифмическая амплитудно-частотная характеристики колебательного звена.
По мере увеличения ξ, длительность переходного процесса увеличивается, частота колебаний уменьшается и при 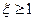 процесс может быть описан ДУследующего вида:
процесс может быть описан ДУследующего вида:
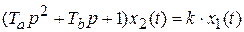 или
или
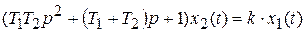 ,
,
где 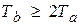 ,
, 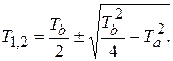
Такое звено называется апериодическим звеном 2-го порядка. Передаточная функция звена определяется выражением
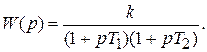
Апериодическое звено 2ого порядка может быть представлено как два последовательно соединенных апериодических звена 1ого порядка. Характеристики звена:
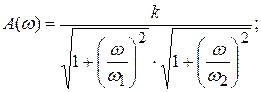
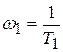 и
и 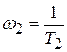 – сопрягающие частоты.
– сопрягающие частоты.
ЛАЧХ (рис.3.9): 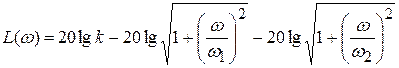
ФЧХ: 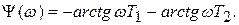
Переходная характеристика (рис.3.9): 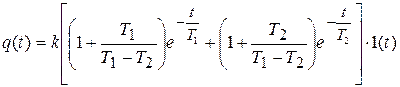 .
.

Рис. 3.9. Переходная и логарифмическая амплитудно-частотная характеристики апериодического звена 2-го порядка
Дифференцирующие звенья.К идеальным дифференцирующим звеньям
относят звенья, выходная величина которых пропорциональна производной входной величины:
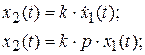
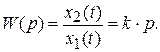
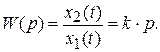
В автоматических системах единственным примером идеального дифференцирующего звена является тахогенератор.
Величина k имеет размерность времени, называется постоянной времени дифференцирования и обозначается Т.
Она может быть определена, если входные и выходные величины имеют одну и ту же физическую природу следующим образом: постоянная времени определяется как интервал времени от момента подачи на вход линейно изменяющегося напряжения до момента времени, когда напряжение на выходе сравняется с напряжением на входе (рис. 3.10).


Рис.3.10. К определению постоянной времени идеального дифференцирующего звена
Характеристики идеального дифференцирующего звена:
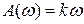 ;
; 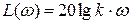 ;
; 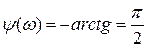 ; q(t) = k δ(t);
; q(t) = k δ(t);
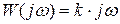 .
.

Рис. 3.11. ЛАЧХ идеального дифференцирующего звена
К инерционным дифференцирующим звеньям относятся звенья, имеющие следующие характеристики:
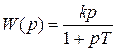 ;
; 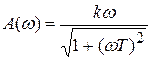 ;
; 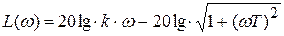 ;
; 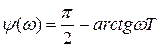 .
.

Рис.3.12. Переходная характеристика инерционного
дифференцирующего звена

Рис. 3.13. ЛАЧХ инерционного дифференцирующего звена
Примером инерционного дифференцирующего звена является RC цепь (рис. 3.13).

Рис. 3.14. Схема инерционного дифференцирующего звена
Форсирующее звено представляет собой параллельное соединение безынерционного и идеального дифференцирующего звеньев:
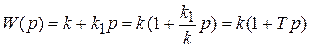 .
.
Звено используется для коррекции передаточных функций систем (компенсирует запаздывание фазы, вносимое интегрирующими звеньями).
Характеристики звена (рис.3.14):
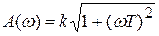 ;
;
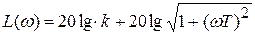 ;
; 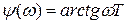 .
.

Рис. 3.15. Характеристики форсирующего звена
Интегрирующие звенья. К идеальным интегрирующим звеньям относят звенья, выходная величина у которых равна интегралу от входной величины:
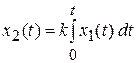 ;
;
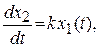
где 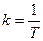 ; Т – постоянная времени звена.
; Т – постоянная времени звена.
Если физическая природа входной и выходной величин одинакова (например, напряжение) постоянная времени определяется как интервал времени от момента подачи на вход постоянного напряжения до момента времени, когда напряжение на выходе сравняется с напряжением на входе ( рис.3.15).


Рис.3.16. К определению постоянной времени идеального
интегрирующего звена
Характеристики идеального интегрирующего звена (рис. 3.16) определяются следующими выражениями:
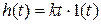 ;
; 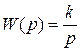 ;
; 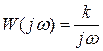 ;
; 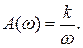 ;
;
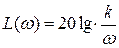 ;
; 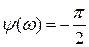 .
.
Примером такого звена является исполнительный двигатель, у которого угол поворота ротора равен интегралу от входного напряжения.

Рис.3.17. Характеристики идеального интегрирующего звена
К инерционным интегрирующим звеньям относятся звенья, передаточная функция которых определяется выражением:
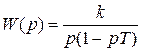 ;
;
Другие характеристики звена (рис.3.17):
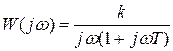 ;
; 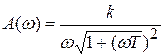 ;
;
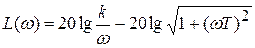 ;
; 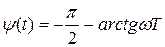
Это звено можно рассматривать как последовательное соединение апериодического звена 1-го порядка и идеального интегратора.

Рис.3.18. Характеристики инерционного интегрирующего звена
Изодромное звено представляет параллельное соединение безынерционного и идеального интегрирующего звеньев:
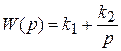 =
= 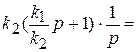
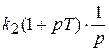
где 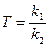 .
.
Характеристики звена:
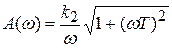 ;
; 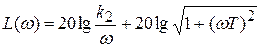 ;
; 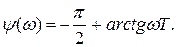
Переходная характеристика и ЛАЧХ звена изображены на рис.3.18.

Рис.3.19. Характеристики изодромного звена
Звено временного запаздывания не входитв приведенную выше классификацию, однако вследствие широкого применения в схемах следящих систем целесообразно привести его характеристики:
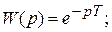
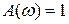 ;
; 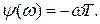 .
.
Звено может быть представлено как n последовательно соединенных апериодических звеньев 1 – го порядка.
Дата добавления: 2020-10-25; просмотров: 526;











