Метод наибольшего давления в пузырьке газа

Основан на измерении давления, при котором происходит отрыв пузырька газа (воздуха), выдуваемого в жидкость через капилляр.

Силы поверхностного натяжения препятствуют образованию пузырька (при этом создаётся новая поверхность раздела фаз жидкость - газ). При медленном продавливании пузырька из капилляра в жидкость в нем возникает избыточное внутреннее давление, которое определяется поверхностным натяжением жидкости и кривизной поверхности пузырька. В момент отрыва пузырька от кончика капилляра внутреннее давление максимально и пропорционально σ.

Измерения проводят на приборе Ребиндера^(*) (см. рис.2.9). Кончик капилляра погружают в жидкость так, чтобы он лишь касался жидкости и приподнимал мениск вверх на 1 - 2 мм. При таком условии поправкой на гидростатическое давление при образовании пузырьков можно пренебречь. Измеряют давление Р₀, необходимое для выдавливания пузырька газа в жидкость с известным поверхностным натяжением σ₀ (обычно воды), а затем - Р_e исследуемой жидкости.

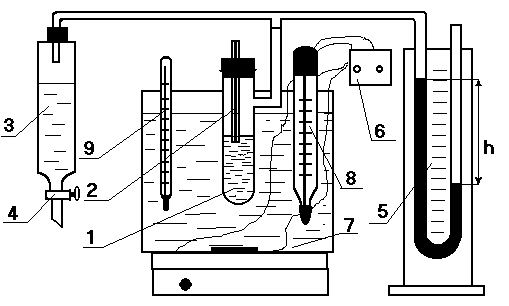
Рис.2.9. Схема установки для измерения поверхностного натяжения методом наибольшего давления в пузырьке газа:

1 – измерительная ячейка, 2 – капилляр, 3 – аспиратор, 4 – кран, 5 – манометр, 6 – регулятор температуры, 7 – термостат, 8 – контактный, 9 – термометр

Под действием приложенного извне избыточного давления ΔР через капилляр продавливается пузырек воздуха. По мере роста пузырька радиус кривизны уменьшается и становится минимальным при r= r_о (когда поверхность пузырька принимает форму полусферы). При увеличении объема пузырька радиус кривизны возрастает r> r_о, следовательно, капиллярное давление Р_σ=2σ/r при r= r_о достигает максимума Р_σ=2σ/r_о.

При ΔР> 2σ/r_о капиллярное давление не может уравновесить приложенного давления ΔР, и пузырёк теряет устойчивость:

σ= ½ ΔР_max r_о

Нужно вводить поправки на сферичность поверхности.

Метод отрыва кольца (Дю-Нуи). Измеряется усилие F, необходимое для отрыва от поверхности жидкости тонкого кольца r_k, хорошо смачиваемого жидкостью (θ=0). Метод похож на метод Вильгельми:

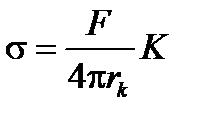, (2.24)

где К – поправочный коэффициент., зависит от геометрии кольца.