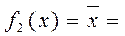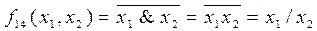Переключательные функции одного и двух переменных
Логические основы информатики. Основные понятия и определения
1.1. ЭВМ— программно-управляемый цифровой автомат
Внедрение цифровых устройств явилось огромным достижением ученых и инженеров конца ХХ века. Их преимущество над аналоговыми основано на следующих факторах:
цифровые устройства допускают большую степень интеграции в составе микросхем, в настоящее время в одной микросхеме размещают десятки миллионов транзисторов;
в отличие от аналоговых устройств данные в цифровых устройствах не зависят от температуры окружающей среды, влажности, давления, напряжения питания;
точность цифровых устройств неограниченна, в настоящее время выпускаются 64- и 128-разрядные процессоры, относительная точность которых составляет 10-12.
Электронные цифровые машины с программным управлением представляют собой пример одного из наиболее распространенных в настоящее время типов преобразователей дискретной информации, называемых дискретными и или цифровыми автоматами. С точки зрения пользователя вычислительная машина представляется в виде некоего «черного ящика», выполняющего достаточно сложные и многочисленные операции при решении самых разнообразных задач. О том, как устроен этот «черный ящик», можно получить достаточно подробные сведения, проведя тщательный анализ процессов представления, преобразования и переработки информации. Необходимо выделить несколько важных положений.
1. Прежде всего, любая вычислительная машина (ВМ) работает автоматически (будь то большая или малая ЭВМ, персональный компьютер, микропроцессор или Супер-ЭВМ). В этом смысле ВМ как автомат может быть описана структурной схемой, представленной на рис. 1.1. Элементы этой структурной схемы применительно к электронным вычислительным машинам (ЭВМ) универсального назначения могут быть определены следующим образом (рис. 1.2).

Рис. 1.1. Обобщенная блок –схема автомата
В качестве исполнительных элементов в автомат включаются;
— арифметико-логическое устройство (AЛУ);
— память;
— устройства ввода—вывода информации.
Управляющим элементом автомата является устройство управления (УУ), которое собственно обеспечивает автоматический режим работы.
Вспомогательными устройствами автомата могут быть всевозможные дополнительные средства, улучшающие или расширяющие возможности автомата.

Рис. 1.2. Структурная схема ЭВМ
Это положение подкрепляет две фундаментальные идеи. Первая состоит в том, что ЭВМ — автомат для переработки и преобразования цифровой или дискретной информации. Это означает, что вся подаваемая на вход ЭВМ информация (текстовая, графическая, числовая и т. п.) должна быть преобразована в набор цифр или чисел, представленных в выбранной системе счисления. Вторая идея заключается в том, что ЭВМ управляется специальной программой, которая может либо вводится в ЭВМ, либо храниться в ее памяти. Программа выполняется автоматически команда за командой (ЭВМ — программно-управляемый цифровой автомат). Следует подчеркнуть очень важные функции памяти ЭВМ.
Память (запоминающее устройство) — функциональная часть ЭВМ предназначенная для хранения и (или) выдачи входной информации, промежуточных и окончательных результатов, вспомогательной информации.
В памяти машины находятся также программы решения задач, через команды которых осуществляется управление работой всей машины.
Основные параметры, характеризующие память, — емкость и время обращения к памяти.
Емкость памяти — количество слов информации, которое можно записать в память. При этом словом является упорядоченная последователь символов алфавита конечной длины. Ячейка памяти — часть памяти содержащая слово.
Ёмкость памяти можно выразить количеством содержащихся в ней слов или ячеек. Длина ячейки памяти измеряется количеством битов (один бит равен одному двоичному разряду) или байтов (один байт содержит восемь битов). Ячейка памяти может вмещать информацию разной длины или разного формата. Формат измеряется словом, двойным словом или полусловом в зависимости от принятого для данной ЭВМ способа представления информации.
Время обращения — интервал времени между началом и окончанием ввода (вывода) информации в память (из памяти). Оно характеризует затраты времени на поиск места и запись (чтение) слова в память (из памяти).
Для построения запоминающих устройств в качестве физических элементов используют электронные схемы, ферритовые магнитные материалы, магнитные ленты и диски, оптические запоминающие элементы и т. д.
Основным преобразователем цифровой информации являемся арифметико - логическое устройство АЛУ. Арифметико-логическое устройство (АЛУ) — функциональная часть ЭВМ, которая выполняет логические и арифметические действия, необходимые для переработки информации, хранящейся в памяти. Оно характеризуется временем выполнения элементарных операций; средним быстродействием т. е. количеством арифметических или логических действий (операций), выполняемых в единицу времени (секунду); набором элементарных действий, которые оно выполняет. Важной характеристикой AЛУ является также система счисления, в которой осуществляются все действия.
В современных вычислительных устройствах основным исполнительным элементом является процессор (П) или микропроцессор (МП), который содержит в себе АЛУ, память (как правило, оперативную память), блок управления.
Устройство управления (УУ) - часть центрального процессора. Оно вырабатывает распределенную во времени и пространстве последовательность внутренних и внешних управляющих сигналов, обеспечивающих выборку и выполнение команд. Эти команды задают последовательность простейших низкоуровневых операций, таких как пересылка данных, сдвиг данных, установка и анализ признаков, запоминание результатов др. Такие элементарные низкоуровневые операции называют микрооперациями, а команды, формируемые устройством управления, называют микрокомандами. Последовательность микрокоманд, соответствующая одной команде, называется микропрограммой.
Для формального описания цифрового автомата широко применяют аппарат алгебры логики, являющейся одним из важных разделов математической логики.
Основные понятия и определения алгебры логики
Основное понятие алгебры логики — высказывание. Высказывание —некоторое предложение, о котором можно утверждать, что оно истинно или ложно. Например, высказывание «Земля — это планета Солнечной системы» ИСТИННО, а о высказывании «на улице идет дождь» можно сказать, истинно оно или ложно, если указаны дополнительные сведения о погоде в данный момент.
Любое высказывание можно обозначить символом х и считать, что х= 1, если высказывание истинно, а х = 0 — если высказывание ложно.
Логическая {булева) переменная — такая величина х, которая может принимать только два значения: х = {0,1}.
Высказывание абсолютно истинно, если соответствующая ей логическая величина принимает значение х = 1 при любых условиях. Пример абсолютно истинного высказывания — высказывание «Земля – планета Солнечной системы».
Высказывание абсолютно ложно, если соответствующая ей логическая величина принимает значение х = 0 при любых условиях.
Например, высказывание «Земля — спутник Марса» абсолютно ложно.
Логическая функция (функция алгебры логики) — функция f(х1, х2,..,хn), принимающая значение, равное нулю или единице на наборе логических переменных x1, x2, ..., xn .
В ЭВМ обрабатывается числовая информация, представленная в двоичной системе счисления (0 и 1). Любую схему ЭВМ можно рассматривать как устройство, имеющее n входных сигналов и m выходных. Поступления на входы некоторой последовательности 0 и 1 вызывает появление на выходах вполне определенной последовательности 0 и 1.
В ЭВМ различают два больших класса схем: класс комбинационных (логических) схем и класс конечных автоматов. В комбинационных схемах значение выходных сигналов в момент времени t однозначно определяется входными сигналами в тот же момент времени. В конечных автоматах выходные сигналы определяются не только входными сигналами, но и состоянием схемы (конечные автоматы содержат элементы памяти).
Построение схем ЭВМ решается с помощью аппарата математической логики. При этом используется только самая простая ее часть – алгебра логики. Основным понятием в той части алгебры логики, на которой основывается ее применение к построению схем ЭВМ, является понятие переключательной функции.
| Таблица 1.1 |
| x1 | x2 | x3 | f(x1,x2,x3) |
Переключательной или булевой функцией называется функция f(x1, ,x2, … xn), способная принимать как и ее аргументы x1, … , xn только два значения
0 или 1. Любая переключательная функция (ПФ) может быть задана таблицей ее значений в зависимости от значений ее аргументов. Такая таблица называется таблицей истинности.
Пример. Зададим ПФ трех аргументов f(x1, x2, x3). Так как каждый из аргументов принимает лишь 2 значения, поэтому мы имеем 8 различных комбинаций 3 переменных. Эти комбинации называют набором. Наборы обычно пишут в так называемом естественном порядке, когда наборы принимают значения (000), (001), … Для получения следующего набора прибавляют 1 к правому разряду – применяется как бы сложение чисел. Наборам присваивается номер, равный двоичному числу, соответствующему данному набору. Сопоставляя каждому набору одно из двух значений ПФ, мы и получим таблицу истинности (например, представленную в табл.1.1).
|
Возьмем какую либо комбинационную схему (КС) (рис.1.3).
 |
Рис.1.3. Комбинационная схема
Если значения ПФ отождествить с выходным сигналом КС, а аргументов - с входными сигналами, то ПФ будет описывать процесс преобразования входных сигналов в выходные, т.е.
y1 = f1(x1,x2,…,xn);
y2 = f2 (x1,x2,…,xn);
.
ym = fm (x1,x2,…,xn).
Любые сложные схемы ЭВМ строятся из простых схем, которые называют логическими элементами.
Логическим элементом называется электронная схема, реализующая элементарную ПФ, имеющая количество входов, равное числу аргументов ПФ и только один выход.
При составлении сложных схем используют два приема: последовательное соединение элементов и перестановку входов элементов. Последовательное соединение логических элементов показано на рис.1.4. 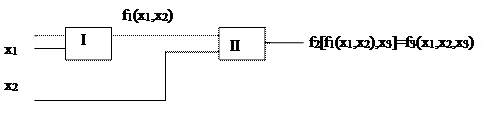
Рис.1.4. Последовательное соединение элементов
Последовательное соединение двух логических элементов позволяет получить функцию f3 трех аргументов. Подстановка в функцию вместо ее аргументов других функций называется суперпозицией.
Перестановка входов элементов показана на рис.1.5.
В общем случае функция f4(x1,x2,x3) отличается от функции f3(x1,x2,x3). Замена одних аргументов функции другими или изменение порядка записи аргументов называется подстановкой аргументов.

Рис.1.5. Перестановка входов элементов
В алгебре логики доказывается, что из ПФ одного и двух аргументов с помощью операций суперпозиции и подстановки можно получить все ПФ от большого числа аргументов. Практически это означает, что из логических элементов с одним и двумя входами можно построить любую сколь угодно сложную комбинационную схему.
Переключательные функции одного и двух переменных
Рассмотрим некоторые ПФ одного и двух аргументов. В табл. 1.2 представлены все 4 функции одного аргумента.
Таблица 1.2
| x | f0(x) | f1(x) | f2(x) | f3(x) |
|
ù х (читается не х).
Все ПФ двух аргументов приведены в табл.1.3.
Таблица 1.3
| х1 | х2 | f0 | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 | f11 | f12 | f13 | f14 | f15 |
Функции f0(x1,x2) и f15(x1,x2) не зависят от значений аргументов: f0(x1,x2)=0 и f15(x1,x2)=1. Функции f3(x1,x2), f5(x1, x2), f10(x1,x2) и f12(x1,x2) являются фактически функциями одного аргумента:

 f3(x1,x2)=x1, f5(x1,x2)=x2, f10(x1,x2)=x2 и f12(x1,x2)=x1.
f3(x1,x2)=x1, f5(x1,x2)=x2, f10(x1,x2)=x2 и f12(x1,x2)=x1.
Рассмотрим часто встречающиеся ПФ. Функция f1(x1,x2) реализует операцию конъюнкции или логического произведения. Как видим из табл.1.3 , функция f1(x1,x2) равна 1, когда и x1 и x2 равны 1. Конъюнкция обозначается как
f1(x1,x2)=x1 & x2 = x1 Ù x2 = x1 x2 (читается x1 и x2).
Функция f7(x1,x2) реализует операцию дизъюнкцию или логического сложения. Функция равна 1, когда или x1 или x2 равны 1. Дизъюнкция обозначается как
f7(x1,x2)=x1 Ú x2.
 Функция f14(x1,x2) реализует операцию отрицания конъюнкции. Из табл.1.3 видно, что когда конъюнкция f1(x1,x1) равна 0, то функция f14(x1,x2) равна 1, а если f1(x1, x2) равна1, то f14(x1,x2) равна 0, т.е. f14(x1,x2)=f1(x1,x2). Эта операция получила название “штрих Шеффера” и обозначается различными способами:
Функция f14(x1,x2) реализует операцию отрицания конъюнкции. Из табл.1.3 видно, что когда конъюнкция f1(x1,x1) равна 0, то функция f14(x1,x2) равна 1, а если f1(x1, x2) равна1, то f14(x1,x2) равна 0, т.е. f14(x1,x2)=f1(x1,x2). Эта операция получила название “штрих Шеффера” и обозначается различными способами:
|
Функция f8(x1, x2) реализует операцию отрицания дизъюнкции. По аналогии с функцией отрицания конъюнкции, из табл.1.3 видно, что f8(x1, x2)=f7(x1, x2). Эта операция также получила отдельное название – “стрелка Пирса” и обозначается следующим образом:
 | |||
|
Функция f6(x1, x2) реализует операцию логической неравнозначности или еще ее называют суммой по модулю два. ПФ равна 1, если аргументы x1 и x2 не равны между собой.
Остальные ПФ двух аргументов рассматривать не будем. В действительности, для реализации сколь угодно сложной ПФ не обязательно использовать все 16 ПФ двух аргументов. Можно ограничиться некоторым набором, с помощью которого можно строить любые ПФ.
Система ПФ, из которых с помощью операций суперпозиции и подстановки можно получить любую сколь угодно сложную ПФ, называется функционально полной системой переключательных функций (ФПС ПФ). Существует несколько ФПС ПФ:
- дизъюнкция, конъюнкция и отрицание;
- отрицание конъюнкции;
- отрицание дизъюнкции и другие.
Возникает вопрос, какие ФПС ПФ представляют наибольший практический интерес? Выбор ФПС ПФ с технической точки зрения эквивалентен выбору типов логических элементов, из которых может быть построена любая логическая схема. Оказывается, что наиболее удобной для решения задач синтеза схемы является ФПС ПФ, содержащая дизъюнкцию, конъюнкцию и отрицание.
Вопросы по лекции
1. В чем достоинства цифровой электроники по сравнению с аналоговой?
2. Что называется автоматом?
3. Что означает выражение «ЭВМ – программно управляемый автомат»?
4. Расскажите о функциональной структуре ЭВМ.
5. Расскажите о назначении и характеристиках памяти ЭВМ. Виды памяти.
6. Расскажите о назначении и характеристиках АЛУ ЭВМ.
7. Расскажите о назначении и характеристиках УУ ЭВМ.
8. Как связаны законы математической логики с принципами организации ЭВМ?
9. Что такое переключательная функция?
10. Как задается переключательная функция?
11. Что такое комбинационная схема?
12. Что такое базис?
13. Что такое инверсия?
14. Что такое булев базис?
15. Что такое универсальный базис?
16. Сколько переключательных функций 1-го аргумента?
17. Сколько переключательных функций 2-х аргументов?
18. При каких значениях аргументов переключательная функция конъюнкция равна 1?
19. При каких значениях аргументов переключательная функция дизъюнкция равна 1?
20. Что такое ФПС ПФ?
21. Определите число различных ПФ при n =4;
22. Постройте таблицу истинности для:

23. Постройте таблицу истинности для:
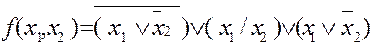
24. Постройте таблицу истинности для:

25. Постройте таблицу истинности для:

26. Постройте таблицу истинности для:
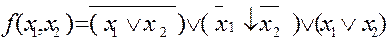
27. Постройте таблицу истинности для:
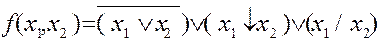
Дата добавления: 2020-10-25; просмотров: 810;