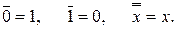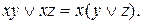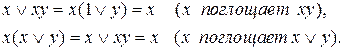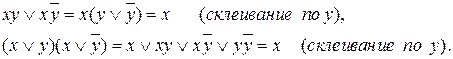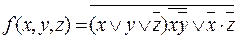Понятие синтеза комбинационных схем

Устройство, работа которого может быть представлена на языке алгебры высказываний, принято называть логическим. Пусть такое устройство имеет n выходов и m входов. На каждый вход может быть подан произвольный символ конечного множества Х, называемого входным алфавитом. Совокупность входных символов, поданных на входы устройства, образует входное слово Р_i в алфавите Х. На выходе устройства появляются выходные слова Q_j, составленные из символов выходного алфавита Y. В силу конечности алфавитов X, Y и слов Pi, Qj (длина слова всегда равна m, а выходного слова - h) общее количество различных входных и выходных слов также конечно.

Элементарный такт работы устройства состоит в том, что при появлении на входе слова Р_i устройство выдает на выходах комбинацию символов Y_i, образующих слово Q_j. Если слово Q_j определяется только входным словом на данном такте, то устройство называется конечным автоматом без памяти, или комбинационной схемой.

Алгоритм функционирования комбинационного устройства будет определен, если задать таблицу соответствия {P_i}->{Q_j} для всех слов P_i. Если входной алфавит X состоит из K различных символов, в таблице соответствия будет K m строк. Так как символы входного и выходного алфавитов принимают только два значения (в данном случае «1» или «0»), то при синтезе и анализе логического устройства применяется булева алгебра.

Под синтезом комбинационной схемы подразумевается построение логической схемы проектируемого устройства в заданном базисе логических элементов. Исходным материалом к синтезу является словесное описание работы устройства.

Синтез комбинационных схем связан с преобразованиями логических выражений, которые содержат ПФ. Приведем достаточно очевидные формулы для ФПС ПФ, содержащей операции дизъюнкции, конъюнкции и отрицания.

Формулы для отрицания:

Формулы для дизъюнкции:

Формулы для конъюнкции:

Правило действия со скобками:

Операция поглощения:

Операция склеивания:

Формулы де Моргана:

Приведенные соотношения дают правила преобразования логических выражений, с помощью которых получают эквивалентные выражения. Новые выражения могут оказаться проще, а это приведет к экономии оборудования и повышению быстродействия устройств ЭВМ.

Пример 2.1. Выражение

можно упростить следующим образом: