Закон Ома и Джоуля-Ленца в классической электронной теории

Основные положения классической теории

Электропроводности металлов

Согласно теории Друде-Лоренца носителями тока в металлах являются свободные электроны, что объясняет высокую электропроводность металлов. Ионы в процессе протекания тока через металл участия не принимают. Если бы это было так, то протекание тока через металл сопровождалось переносом вещества. В действительности этого не наблюдается (опыт Рикке).

Основные положения классической электронной теории металлов следующие:

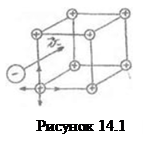1. Металлы имеют кристаллическую решётку, в узлах которой находятся положительные ионы (рис.14.1). Эти ионы не могут перемещаться по кристаллу, а испытывают лишь небольшие колебания около своих положений равновесия.

2. Между узлами кристаллической решётки движутся свободные электроны, называемые электронами проводимости.

3. При наличии внешнего электрического поля Е на хаотическое движение свободных электронов накладывается их упорядоченное (направленное) движение – так называемый дрейф электронов в определённом направлении.

4. Электроны проводимости при своём движении сталкиваются с ионами решётки, столкновения между электронами проводимости не учитывается.

5. Внешнее поле не влияет на концентрацию носителей тока и среднее время их свободного пробега.

Закон Ома и Джоуля-Ленца в классической электронной теории

Согласно закону равномерного распределения энергии по степеням свободы, на один электрон приходится средняя кинетическая энергия теплового движения

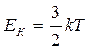
( k - постоянная Больцмана, Т – температура (на каждую степень свободы приходится энергия, равная 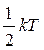, электрон рассматривается как материальная точка; следовательно, свободный электрон обладает тремя степенями свободы)).

При тепловом движении электроны испытывают соударения.

Путь, проходимый электронами между двумя последовательными соударениями, называют длиной свободного пробега <ℓ>(рис.14.2).

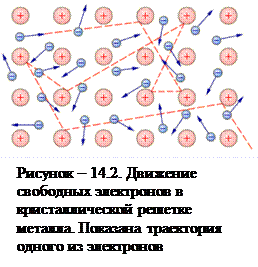Предположим, что при каждом соударении электрон полностью передаёт свою энергию ионам решётки и начальная скорость последующего движения электрона равна нулю.

Если по проводнику течёт постоянный ток, то внутри проводника существует электрическое поле, напряжённостью Е. На каждый электрон со стороны электрического поля действует сила F=eE, где е – заряд электрона. Под действием этой силы электрон приобретает ускорение а, которое можно определить из равенства m_ea =еЕ, откуда

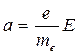(14.1)

( m_e - масса электрона).

Если <t>– среднее время между двумя последовательными соударениями, то к концу свободного пробега электрон приобретает скорость

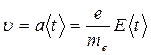(14.2)

Средняя скорость упорядоченного движения электронов

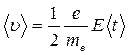(14.3)

(начальная скорость считается равной нулю, поэтому движение равноускоренное).

Среднее время между двумя последовательными соударениями можно определит, если знать длину свободного пробега и среднюю скорость теплового движения <υ_τ>:

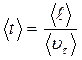(14.4)

Вообще, 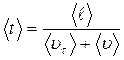, но соотношение (14.4) справедливо, так как уже было показано, что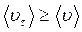

Подставив <ℓ> из (3.99) в формулу (3.98), получим

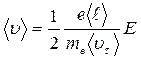(14.5)

Подставив в формулу j = ne<υ> (13.37) , получим

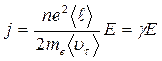(14.6)

(где

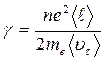(14. 7)

- удельная проводимость материала проводника (величина, обратная его удельному сопротивлению)).

v Единица удельной проводимости – сименс на метр (См/м)

Из выражения (3.101), представляющего закон Ома, следует: плотность тока пропорциональна напряжённости электрического поля, что совпадает с (3.81).

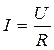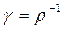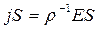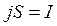Из формулы (3.101) легко получить закон Ома в виде , для этого её правую и левую части надо умножить на S – площадь поперечного сечения проводника. Учитывая, что , получаем , но , а 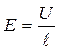(поле внутри проводника длиной ℓ считаем однородным); следовательно,

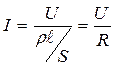(14.8)