Приведение к нормальным формам
Как, анализируя формулу в нормальной форме, можно сделать вывод о ее общезначимости или невыполнимости? Возьмем ДНФ, т.е. представление формулы в виде дизъюнкции конъюнкций К1ÚК2Ú...ÚKn. Для того, чтобы сделать вывод о ее общезначимости, нужно анализировать всю формулу целиком: каждая конъюнкция общезначимой формулы может быть истинной только на нескольких интерпретациях. В то же время, вывод о невыполнимости дизъюнкции конъюнкций можно сделать легко: каждая конъюнкция ДНФ невыполнимой функции должна быть невыполнима, а это очень легко проверить: конъюнкция литер невыполнима тогда и только тогда, когда она содержит хотя бы одну пару противоположных литер. Полностью аналогично можно использовать представление в виде КНФ, но для определения общезначимости функции. Очевидными следствиями предыдущих теорем являются:
Теорема 2.3 Для того, чтобы формула R была логическим следствием формул F1, F2, ..., Fk, необходимо и достаточно, чтобы каждый конъюнкт дизъюнктивной нормальной формы представления формулы F1F2...FkØR содержал пару противоположных литер. ÿ
Теорема 2.4 Для того, чтобы формула R была логическим следствием формул F1, F2, ..., Fk, необходимо и достаточно, чтобы каждый дизъюнкт конъюнктивной нормальной формы представления формулы F1F2...FkÞR содержал пару противоположных литер. ÿ
Пример 2.7 Докажем правильность схемы рассуждения “Узнала - спросила” примера 2.4 приведением к ДНФ: (ØСкÞØУ) (ØСпÞØСк)УØСп = (СкÚØУ)(СпÚØСк)УØСп =
(СкСпУØСп) Ú (СкØСкУØСп) Ú (ØУСпУØСп) Ú (ØУØСкУØСп).
Поскольку каждый конъюнкт содержит пару противоположных литер, эта формула невыполнима, и, следовательно, схема рассуждения “Узнала - спросила” правильна. Заметим, что это доказательство много проще построения и анализа таблиц истинности (таб.2.6). ÿ
Метод резолюции
Этот метод использует тот факт, что если некоторая формула является невыполнимой, то наиболее сильное следствие этой формулы - константа False. Предложенный в 1965г. Дж. Робинсоном [R65] метод резолюции позволяет получить максимально сильное следствие множества формул с помощью систематической процедуры последовательного построения логических следствий формулы, называемых резольвентами. Иными словами, метод резолюции обладает свойством полноты: для формулы Ф следствие Falseобязательно будет получено, если Ф - невыполнима.
Теорема 2.4. Пусть В - логическое следствие формулы А. Тогда А&В º А.
Доказательство теоремы легко проводится на основании определения понятия логического следствия. Действительно, пусть условие теоремы выполнено. Тогда в соответствии с теоремой 2.1, АÞВ º True. Отсюда АºА&TrueºА&(АÞВ) ºА(ØАÚВ) ºА&ØАÚА&ВºFalseÚА&ВºА&В. ÿ
Определение 2.5. Резольвентой двух дизъюнктов D1ÚL и D2ÚØL называется дизъюнкт D1ÚD2. ÿ
Теорема 2.5. Резольвента является логическим следствием порождающих ее дизъюнктов.
Доказательство. Пусть D1ÚL и D2ÚØL - два дизъюнкта. Тогда D1ÚD2 - их резольвента. Легко показать, что формула (D1ÚL)&(D2ÚØL)Þ(D1ÚD2) общезначима. По теореме 2.1 отсюда следует заключение теоремы. ÿ
Метод резолюции доказательства невыполнимости формулы Ф=F1F2...FkØR состоит в том, что формула Ф представляется в КНФ, и к ней конъюнктивно присоединяются все возможные резольвенты ее дизъюнктов и получаемых в процессе доказательства резольвент. Полнота метода резолюции состоит в том, что он гарантирует получение для формулы Ф следствия False, если Ф - невыполнима. Если же, перебрав все возможные резольвенты формулы Ф, мы не нашли пустую резольвенту, то Ф не является невыполнимой.
Пример 2.8. Доказательство правильности рассуждения “Узнала - спросила” сводится к проверке невыполнимости формулы Ф=F1&F2&F3&ØR, где F1=ØСкÞØУ, F2=ØСпÞØСк, F3=У и R= Сп.
Перечислим все дизъюнкты конъюнктивной нормальной формы Ф и построим возможные резольвенты:
| N | Дизъюнкт | Откуда он получен | Интерпретация |
| (1) | СкÚØУ | - первое утверждение: | Известно, что: “Если бы он не сказал ей, она бы не узнала”; |
| (2) | СпÚØСк | - второе утверждение: | и что “Если бы она его не спросила, он бы не сказал ей”; |
| (3) | У | - третье утверждение: | и что “Она узнала”. |
| (4) | ØСп | - отрицание следствия: | Докажем, что "Она спросила”. Предположим противное,т.е. что "Онане спросила”. |
| (5) | ØСк | - резольвента 2 и 4; | Отсюда следует (поскольку по (2): “Если бы она его не спросила, он бы не сказал ей”)что "Он не сказал ей". |
| (6) | ØУ | - резольвента 1 и 5; | Отсюда следует (поскольку по (1):“Если бы он не сказал ей, она бы не узнала”)что "Она не узнала". |
| (7) | ÿ | - резольвента 3 и 6, пустой дизъюнкт | Мы пришли к противоречию: ведь известно же (3), что“Она узнала”. Следовательно, нашепредположениеневерно (оно противоречит фактам), т.е. "Онане спросила”. |
Доказательство методом резолюции сделаем более наглядным, представив его графически:
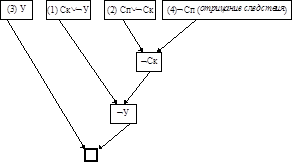
Рис.2.2. Графическое представление доказательства методом резолюции
Доказательство методом резолюции очень близко обычному словесному доказательству от противного. Это демонстрирует интерпретация последовательных формул вышеприведенной таблицы. Проинтерпретируем еще раз это доказательство в естественном языке по графу рис.2.2.
Рассуждение: “Если бы он не сказал ей, она бы и не узнала. А не спроси она его, он и не сказал бы ей. Но она узнала. Следовательно, она спросила.”
Доказательство (см. рис.2.2): “Предположим противное, т.е. что она не спросила. Тогда из второго утверждения следует, что он ей не сказал. Отсюда, и из первого утверждения следует, что она не узнала. Но в третьем утверждении говорится, что она узнала. Таким образом, предположив, что следствие неверно, мы пришли к противоречию. Поэтому следствие верно.”
Для рассуждения примера 2.2: “В хоккей играют настоящие мужчины. Трус не играет в хоккей. Я в хоккей не играю. Значит, я трус(?!)” метод резолюции дает (см таб.2.5):
(1) ØХÚМ - первое утверждение: “В хоккей играют настоящие мужчины”;
(2) МÚØХ - второе утверждение: “Трус не играет в хоккей”;
(3) ØХ - третье утверждение: “Я в хоккей не играю”;
(4) М - отрицание следствия: “Предположим, что неверно, что "Я трус" ”;
Резольвент нет
Мы не можем построить здесь ни одной резольвенты, не говоря уж о пустой. Отсюда можно заключить, что вывод в этом рассуждении не является логическим следствием высказанных утверждений и не следует формально из их истинности. Для доказательства (или опровержения) этого вывода необходимы дополнительные факты.
Определение 2.6. Пусть S - множество дизъюнктов. Резолютивный вывод С из S есть такая конечная последовательность С1,...,Сk дизъюнктов, что Сk = C и каждый дизъюнкт Сi или принадлежит S или является резольвентой дизъюнктов, предшествующих Сi. Вывод пустого дизъюнкта из S называется опровержением S. ÿ
Следующая теорема является важнейшей теоремой теории логического вывода в логике высказываний: она утверждает, что используя единственное правило вывода - резолюцию, мы можем проверить правильность любого заключения из фактов, последовательно получая резольвенты и присоединяя их к исходной формулировке.
Теорема 2.6 (о полноте метода резолюции). Множество дизъюнктов S невыполнимо тогда и только тогда, когда существует резолютивный вывод пустого дизъюнкта из S.
Необходимость. Доказательство того, что при невыполнимости S всегда найдется резолютивный вывод пустого дизъюнкта из S за конечное число шагов, здесь опускается.
Достаточность. Пусть из S существует резолютивный вывод пустого дизъюнкта. Докажем, что S невыполнимо. Поскольку резольвента  есть логическое следствие порождающих ее дизъюнктов Di и Dk, то конъюнктивное присоединение резольвенты  к формуле S не меняет ее значения, поскольку S=ADiDk, а DiDkºDiDk согласно теоремам 2.4 и 2.5. Если среди резольвент Ф существует пустая резольвента, соответствующая ее логическому следствию False,то Ф невыполнима, поскольку эквивалентна формуле с конъюнктивным членом False. ÿ
Перебор всех возможных резольвент можно организовать по-разному, и разные стратегии построения резольвент будут (в среднем) иметь различную эффективность (число шагов вывода до получения положительного или отрицательного ответа). Одной из наиболее эффективных стратегий является стратегия движения “от цели” - получение на каждом шаге резольвент из двух дизъюнктов, один из которых - это цель доказательства (инверсия предполагаемого следствия) или резольвента-потомок этой цели. Эта стратегия особенно эффективна в языках логического программирования, где только небольшое число фактов общей базы данных действительно имеют отношение к заданному вопросу. Мы рассмотрим использование метода резолюции в языках логического программирования ниже.
Другие методы. Использование семантических деревьев для проверки общезначимости или невыполнимости формулы было предложено Куайном. Идея основывается на том, что часто нет необходимости строить все дерево до листьев: в некотором узле значение функции может быть определено сразу для всех листьев, которые могут быть построены из этого узла. Метод Куайна был усовершенствован Девисом и Патнемом, предложившими для проверки невыполнимости формулы предварительно представить эту формулу в КНФ. Функция представляется в виде совокупности дизъюнктов, каждый из которых - просто множество литер, и алгоритм сводится просто к вычеркиванию литер из этих множеств в узлах семантического дерева.
Адекватность логики высказываний. Вопрос об адекватности математической модели при решении конкретных проблем в реальной жизни, как уже говорилось выше, лежит вне самого математического аппарата, это проблема, которую должен решать человек, использующий этот аппарат для решения задач практики. В области формализации рассуждений естественного языка всегда надо быть осторожным, применяя выводы логики высказываний к реальной жизни. Хорошую иллюстрацию этому дает так называемая “задача Кислера”, приведенная в монографии С. Клини “Математическая логика”. Рассмотрим ее в несколько измененной постановке.
Браун, Джонс и Смит обвиняются в преступлении. На допросе они под присягой дали показания:
Браун: Джонс виновен, а Смит невиновен (Д&С).
Джонс: Браун без помощи Смита это не смог бы сделать (БÞC).
Смит: Я невиновен, но кто-то из них виновен (ØC&(БÚД)).
Из этих утверждений следует, что виноват Джонс, а двое других подозреваемых невиновны (докажите!). Но задумаемся, действительно ли мы можем считать эти посылки истинными? Что, если виновный лжет, а невиновный говорит правду? В этом случае нахождение максимально сильного следствия шести посылок:
F1:ØБÞ(Д&С); F3:ØДÞ(БÞC); F5:ØСÞØC&(БÚД);
F2: БÞØ(Д&С); F4: ДÞØ(БÞC); F6: СÞØ(ØC&(БÚД));
приводит к полностью противоположному выводу. Если же мы будем полагаться на информацию только тех, кто невиновен (т.е учитывать только утверждения F1, F3, F5), то мы получим третий результат: установить в точности, кто виновен, без дополнительной информации нельзя. Таким образом, результаты анализа одной и той же ситуации с привлечением одного и того же аппарата - логики высказываний - существенно меняются в зависимости от того, как мы формализуем задачу проверки правильности рассуждений, какие факты мы будем считать установленными.
Другим примером, иллюстрирующим это положение, является доказательство древнегреческого философа Зенона того, что движения нет: “Если тело движется, то движение может происходить либо там, где тело есть, либо там, где тела нет. Но движение не может происходить там, где тело есть, потому что тогда бы оно стояло на месте. Движение не может также происходить там, где тела нет: если там тела нет, то как оно может там двигаться?. Следовательно, тело двигаться не может”. Логическая структура этого доказательства совершенно правильна, но формальная логика не может отвечать за то, что содержание умозаключения неверно. Движение все же есть!
Дата добавления: 2016-07-27; просмотров: 2458;











