Логика высказываний
Формальные модели
Предмет изучения в этой главе - начала математической, или формальной логики. Математическая логика - это наука, которая занимается анализом суждений и доказательств, используемых человеком для обоснования нового знания, произведенного из установленных фактов. В логике используется специально созданный формализованный язык, подчиняющийся своей системе анализа. Логика исследует схемы рассуждений, которые верны в силу одной их формы, независимо от содержания. Фактически, логика - это множество правил манипулирования формулами, представляющими формы рассуждений. Формальная логика игнорирует смысл, содержание предложений естественного языка, для которых формулы логики являются моделями.
Отвлечение от содержания предложений языка в формальной логике есть результат применения операции абстрагирования к рассуждениям естественного языка. Абстрагирование является основным этапом при построении математической модели, оно широко используется в науке для выборочного исследования некоторых аспектов исследуемой проблемы. Цель абстрагирования - выделение тех аспектов, которые существенны для исследования и решения проблемы и игнорирование тех аспектов, которые несущественны, усложняют проблему, делают анализ менее общим или вообще невозможным.
При научном подходе, на уровне рационального исследования, мы имеем дело не с материальными объектами во всем многообразии их свойств, а с абстракциями от материальных объектов. Реальные объекты и ситуации обычно бесконечно сложны, и абстракция применяется для того, чтобы ограничить эту сложность, дать возможность принимать решения. С помощью абстрагирования человек строит формальные модели самых разнообразных по своей природе понятий, процессов и явлений, сущностей реального мира. Такие формальные модели, будучи построенными, далее допускают анализ и преобразование с помощью формальных же средств: абстракции сами могут быть исследованы с точки зрения их свойств (структура, элемент, отношение, и т.д.), и при таком анализе исследователь может отвлечься от окружающей реальности, оставаясь в рамках построенной им знаковой системы. Формальные модели позволяют выразить некоторые свойства объекта в точных терминах математических определений и аксиом так, что затем можно “вывести” свойства этой модели, которые объяснят известные и предскажут новые свойства исследуемой реальной сущности. Именно на основе научного подхода к решению инженерных проблем получено бессчетное число впечатляющих результатов в технике, в связи с чем давно укоренилась поговорка "Нет ничего более практичного, чем хорошая теория". Получая в результате анализа моделей какие-либо выводы, исследователь пытается применить эти результаты к той области реального мира, отображением которой является модель, построенная в результате абстракции. Поскольку все абстракции неполны и неточны, можно говорить только о приближенном соответствии с реальностью тех результатов, которые получены исследованием на моделях. Соответствие законов движения, связей и отношений объектов модели соответствующим элементам реального мира называется адекватностью, и степень адекватности определяет, применимы ли такие результаты к конкретной проблеме в реальном мире. Часто адекватность модели определяется рядом условий и ограничений на сущности реального мира, и для того, чтобы использовать результаты анализа, полученные на модели, необходимо тщательно проверять эти ограничения и условия (или обеспечить их выполнение).
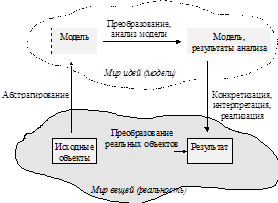
Рис.2.1 Соотношение моделей и реальности
В предыдущей главе стояла проблема построения конечных функциональных преобразователей в реальном мире. Эта проблема была решена полностью в соответствии с рис.2.1. Вместо того, чтобы непосредственно начать строить эти преобразователи из реальных объектов (т.е. использовать чисто эмпирический подход, или подход "тыка"), мы представили эту проблему как задачу построения двоичных функций, реализующих требуемое функциональное отображение (т.е. сначала выполнили абстрагирование). Мы затем использовали систематический метод решения этой математической задачи (преобразование модели). На следующем этапе мы также, рассмотрели, как произвольные двоичные функции могут быть реализованы из электронных переключателей и транзисторов (фактически, мы занимались вопросами конкретизации, реализации абстрактной модели). Адекватность реализации модели логических функций обеспечивается в этой конкретной проблеме поддержанием в определенных границах напряжений и токов в электронных переключателях, определенных временных ограничений на работу переключателей и т. д.. Всеми этими средствами достигается коммутативность диаграммы рис.2.1 в решении этих проблем (коммутативность этой диаграммы мы понимаем здесь как возможность получения одного и того же результата из исходных объектов двумя путями: первый - это непосредственным выполнением преобразований объектов в мире вещей, второй - это выполнением операции “абстрагирование” и переходом в мир моделей, затем выполнением операции “преобразование моделей” и, наконец, выполнением операции “конкретизация” с возвращением в мир реальных объектов).
Отметим, что на рис.2.1 ясно видны различия в задачах фундаментальных и инженерных наук:
* Теоретики занимаются внутренними проблемами теорий: разработкой абстрактных моделей, разработкой методов их преобразования и анализа. Они интересуются проблемами, лежащими на рис.2.1 в области «мира идей». В значительно меньшей степени их интересуют вопросы абстрагирования и адекватности моделей, их интерпретация в различных приложениях.
* Перед инженерами стоит задача построения и анализа реальных объектов, но вместо решения ее непосредственно, они сначала абстрагируются от всех деталей реальности, которые несущественны для решения поставленной проблемы, выбирают модель, которая отражает существенные детали, пользуются разработанными теоретиками методами преобразования и анализа моделей, после чего решают исходную задачу с помощью интерпретации и применения этих теоретических результатов в реальном мире. Для инженеров проблема проверки и обеспечения адекватности используемых моделей является определяющей. Важной является также проблема выбора среди множества формальных моделей такой модели, в рамках которой исходная проблема имеет решение. Чаще всего рамки модели накладывают существенные ограничения на применимость результатов этого подхода в реальном мире. На рис.2.1 область их главных интересов – это проблемы связи мира реального и мира идей, т.е. вопросы адекватного использования существующих моделей для решения конкретных задач практики.
Формальная математическая логика решает проблемы проверки правильности рассуждений в естественном языке (реальный мир), строя свои модели и правила их преобразования. Для этого логика вводит свои языки - систему формальных обозначений (формулы) и правила их преобразования. Поэтому логику можно рассматривать как множество правил манипулирования формулами, описывающими утверждения естественного языка. В результате конкретизации (интерпретации) результатов и выводов формальной логики (новых полученных формул) мы получаем новые предложения естественного языка, можем оценить свойства исходных предложений и т.д. Следует ясно понимать, однако, при каких ограничениях выводы, полученные с помощью формализма математической логики, мы можем использовать в реальной жизни.
Логика высказываний
Из всего разнообразия естественного языка логика высказываний имеет дело только с узким кругом утверждений - повествовательных предложений, которым может быть приписано значение “истина” либо “ложь”. Каждому элементарному утверждению в логике высказываний сопоставляется высказывание, обозначающееся буквой. Истинностные значения, которые можно приписать высказываниям, обычно изображаются “И” и “Л”, “1” и”0” или Trueи False. Кроме простейших высказываний, структура которых не анализируется (они поэтому называются атомами) вводится понятие сложного высказывания или формулы - комбинации более простых высказываний.
Определение 2.1. Формулы логики высказываний определяются рекурсивно над счетным множеством атомов (элементарных высказываний) Á с помощью символов операций (связок) Ø, Þ и скобок “(“ и “)”:
1. Логические константы True, False есть формулы.
2. Любой атом из Á есть формула.
3. Если Р - формула, то Ø(Р) тоже формула.
4. Если Р, Q - формулы, то (PÞQ) - тоже формула.
5. Никаких других формул в логике высказываний нет.ÿ
В логике для сокращения формул используются записи:
(PÚQ) для ((ØP)ÞQ),`
(P&Q) для Ø(Ø(P)Ú(ØQ)),
(PÛQ) для (PÞQ)&(QÞP),
и, кроме того, вводятся правила приоритетов операций для уменьшения скобок в формулах.
Интерпретацией называется придание всем атомам некоторых истинностных значений. Значения формул на всех возможных интерпретациях определяется на основе таблиц истинности для основных символов операций (связок) Ø, Þ:
Таблица 2.1 Таблица 2.2
| Р | ØP | Р | Q | PÞQ | |
| False | True | False | False | True | |
| True | False | False | True | True | |
| True | False | False | |||
| True | True | True |
Совершенно очевидно, что логика высказываний и теория булевых функций имеют теснейшую связь: обе эти модели являются булевыми алгебрами. Истинностные значения True и False в логике соответствуют 1 и 0, пара основных логических связок - отрицание и импликация - составляют базис (базис Фреге), и все остальные производные логические связки соответствуют известным нам булевым функциям. Двоичные переменные, принимающие значения 1 или 0 в теории булевых функций соответствуют высказываниям, принимающим значения True или Falseв логике. Для простоты мы дальше будем пользоваться 1 и 0 или t и f как истинностными значениями и всеми известными нам булевыми функциями в виде логических связок, а также результатами и терминологией, известными нам из теории булевых функций. Логические формулы будем называть логическими функциями (они являются функциями, сопоставляющими каждой интерпретации своих аргументов истинностные значения t или f).
Определение 2.2.Литерой будем называть атом или его отрицание. Две литеры будем называть противоположными, если одна из них является отрицанием другой.ÿ
В формальной логике большую роль играют формулы, принимающие одно и то же значение True на всех интерпретациях. Такие формулы называются общезначимыми или тавтологиями. Формула, принимающая значение False на всех интерпретациях своих аргументов, называется невыполнимой. Импликации в естественном языке соответствует связка “если ... то …”.
При всей похожести теорий, задачи, которые они решают, разные. Теория двоичных функций занимается проблемой реализации преобразователей информации. Формальная логика работает с абстракциями, построенными из предложений и рассуждений естественного языка, и интерпретации ее выводов также лежат в области естественного языка.
Пример 2.1 Проанализируем предложение: “Порядочный человек не может быть вором”. Предложение состоит из двух более простых утверждений, которые мы представим в модели атомами: П - “некто есть порядочный человек”; В - “некто является вором”.
Логическая формула, представляющая приведенное выше предложение, очевидно имеет вид: ПÞØВ. Существует несколько формул, эквивалентных данной: ØПÚØВ; Ø(П&В); ВÞØП. Интерпретируя эти формулы в естественном языке, получим следующие утверждения, которые все эквивалентны между собой:
· ПÞØВ: “Порядочный человек не может быть вором”
· (ØПÚØВ): “Или он не порядочный человек, или же он не вор”;
· Ø(П&В): “Порядочность и воровство несовместимы”;
· ВÞØП: “Если человек вор, то он не является порядочным человеком”.
Другой пример. Утверждение “Симпсон будет признан судом виновным тогда и только тогда, когда все 12 присяжных заседателей признают его виновным” в формульной записи представится так: ВÛ(П1& П2& …&П12). Эквивалентная формула: ØВÛØ(П1& П2& …&П12) по закону де Моргана может быть преобразована так: ØВÛ(ØП1ÚØП2Ú…ÚØП12), что можно интерпретировать как: “Симпсон не будет признан судом виновным тогда и только тогда, когда хотя бы один из 12 присяжных заседателей не признает его виновным”.ÿ
С эквивалентностью этих предложений в естественном языке трудно спорить, но на этом пути все же следует быть осторожным. Например, предложения “Он убил, и ему стало страшно” и “Ему стало страшно, и он убил”, полностью эквивалентные с точки зрения формальной логики, вовсе не эквивалентны в естественном языке. Далее, принятое в формальной логике правило, согласно которому любое высказывание может быть только либо истинным, либо ложным, а третьего не дано, не всегда выполняется в реальной жизни (например, какое истинностное значение приписать предложению “Это предложение ложно”, которое не может быть ни истинным, ни ложным). Особые трудности вызывает соотношение формальной импликации и причинно-следственных отношений в естественном мире. Например, фраза: “Если прошел дождь, то дорога мокрая” утверждает очевидную связь между фактами А (прошел дождь) и В (дорога мокрая), что выражается логической формулой АÞВ. Из житейского опыта мы связываем с этим причинно-следственным отношением также и дополнительное знание: “Если дождя не было, то дорога сухая”, т.е. формула ØАÞØВ тоже справедлива, ее можно считать следствием исходной формулы. Однако две логические формулы АÞВ и ØАÞØВ совершенно различны, из истинности первой формально не следует истинность второй.
Монографии, написанные ведущими специалистами по формальной логике, большое внимание уделяют этой проблеме адекватности - условиям применимости выводов и результатов формальной логики в естественном языке (см., например, [П82]). Результаты формальной логики могут быть применены к высказываниям естественного языка только если выполняются ее постулаты, в частности, высказывания являются только либо истинными, либо ложными (“черно-белый взгляд на мир”), они не включают никаких уровней уверенности-неуверенности и возможности, все причинно-следственные отношения между фактами явно выражены, истинностные значения высказываний статичны, не меняются во времени и т.д. Представляемая здесь ветвь логики формализует лишь самую простую часть тех закономерностей, которым подчиняется мышление и язык. Однако, даже эта часть является удивительной и впечатляющей по своим результатам. Существуют различные интересные расширения классической логики, например, многозначная логика, формализующая конкретный набор степеней уверенности в истинности высказываний, нечеткая логика, в которой можно оперировать с оценками степени уверенности (вероятностями) в истинности высказываний, темпоральная логика, позволяющая формулировать высказываниями о свойствах систем, проходящих изменяющиеся последовательные стадии, и т.д. Эти логики, однако, выходят за рамки нашего рассмотрения.
Дата добавления: 2016-07-27; просмотров: 2184;











