По нормальным и наклонным сечениям

Изгибаемыми называют элементы, подверженные действию одного изгибающего момента или изгибающего момента с поперечной силой.

В качестве примера рассмотрим однопролетную железобетонную балку, свободно лежащую на двух опорах, симметрично загруженную двумя сосредоточенными силами (рисунок 2.19).

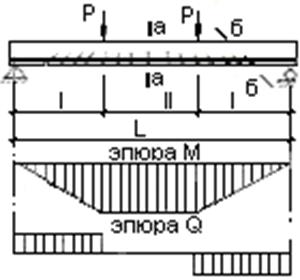Рисунок 2.19- Схема изгибаемого элемента

Участок балки между грузами находится в условиях чистого изгиба; в его пределах действует только изгибающий момент М, поперечная сила Q=0. На определенной ступени загружения в бетоне растянутой зоны этого участка образуются нормальные трещины (направленные перпендикулярно продольной оси балки). На участках одновременного действия М и Q образуются наклонные трещины.

В железобетонных нормально армированных изгибаемых элементах разрушение начинается с растянутой арматуры. По достижении в ней предела текучести резко уменьшается высота сжатой зоны бетона, что вызывает ее разрушение. Лишь в балках с очень большим количеством растянутой арматуры разрушение может начаться со сжатой зоны; при этом напряжения в арматуре будут ниже предела текучести, что экономически невыгодно.

В соответствии с характером разрушения балок по нормальным сечениям различают два случая расчета:

- первый случай, когда расчет ведется в предположении, что первопричиной исчерпания прочности элемента будет достижение в растянутой арматуре расчетных сопротивлений;

- второй случай, когда расчет ведется в предположении, что прочность элемента исчерпывается вследствие разрушения сжатой зоны бетона раньше, чем напряжения в растянутой арматуре достигнут расчетного сопротивления.

Если главные растягивающие напряжения превысят сопротивление бетона растяжению, возникают наклонные трещины.

При дальнейшем увеличении нагрузки наклонные трещины раскрываются и в конечной стадии происходит разрушение элемента вследствие раздробления бетона над вершиной наклонной трещины и развития напряжений в поперечных стержнях-хомутах до предельных значений. Напряжения в продольной арматуре могут и не достигать предельных значений.