ТЕОРЕМА О ГОМОМОРфизМЕ КОЛЕЦ
Пусть К=(К,+,×,1) и К¢=(К¢,+,×,1¢) - кольца, ¦ - гомоморфизм кольца к в кольцо к¢. Обозначим Ker¦={xÎK½¦(x)=0¢}, где 0¢ - нуль кольца К¢. Ker¦ называется ядром гомоморфизма ¦. Покажем, что Ker¦ является, идеалом кольца К. Действительно, Ker¦¹Æ, так как 0Î Ker¦. Для любых а,bÎ Ker¦ имеем ¦(а-b)= ¦(а)-¦(b)=0¢-0¢=0¢, то есть Ker¦ замкнуто в K относительно вычитания. Для любого aÎKer¦ и любого kÎК имеем: ¦(ka)=k¦(a)=k0¢=0¢, то есть kaÎKer¦. аналогично убеждаемся, что akÎ Ker¦. Таким образом, доказано, что Ker¦ есть идеал кольца К. Покажем, что для любых а, b из К равенство ¦(а)=¦(b) выполняется тогда и только тогда, когда 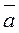 =
= 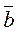 .
.
Пусть ¦(а)=¦(b), тогда ¦(а-b)= ¦(а)-¦(b)=0¢, так как ¦ - гомоморфизм. Поэтому, а-bÎ Ker¦, откуда 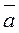 =
= 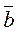 . Теперь допустим, что
. Теперь допустим, что 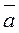 =
= 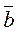 . Тогда а-bÎ Ker¦, откуда ¦(а-b)=0¢, так как Ker¦ - ядро. Отсюда получаем: ¦(а)-¦(b)=0¢ и ¦(а)=¦(b).
. Тогда а-bÎ Ker¦, откуда ¦(а-b)=0¢, так как Ker¦ - ядро. Отсюда получаем: ¦(а)-¦(b)=0¢ и ¦(а)=¦(b).
Теорема. Пусть ¦ - эпиморфизм кольца к на кольцо к¢ с ядром J. Тогда фактор-кольцо к/J изоморфно кольцу к¢.
Доказательство. Пусть K=К/J и K/J=(K/J,+,×, 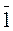 ), где
), где 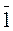 =l+J. Обозначим через j отображение K/J в К¢, определенное следующим образом: j(
=l+J. Обозначим через j отображение K/J в К¢, определенное следующим образом: j( 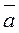 )=¦(а) для каждого элемента
)=¦(а) для каждого элемента 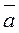 из K/J. В силу предыдущих рассуждений значение j(
из K/J. В силу предыдущих рассуждений значение j( 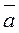 ) не зависит от выбора представителя а в смежном классе
) не зависит от выбора представителя а в смежном классе 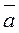 . Далее, отображение j сохраняет главные операции кольца к/J. В самом деле, j(
. Далее, отображение j сохраняет главные операции кольца к/J. В самом деле, j( 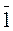 )==1к', и для любых
)==1к', и для любых 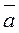 ,
, 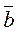 из К/J имеем: j(
из К/J имеем: j( 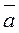 +
+ 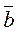 )=j(
)=j( 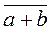 )=¦(a+b)= ¦(a)+¦(b) =j(
)=¦(a+b)= ¦(a)+¦(b) =j( 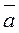 )+j(
)+j( 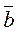 ); j(-
); j(- 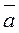 )=j(
)=j( 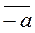 )=¦(-a)=-¦(a)=-j(
)=¦(-a)=-¦(a)=-j( 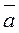 ); j(
); j( 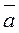 ×
× 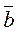 )=j(
)=j( 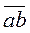 ) =¦(a×b)=¦(a)צ(b)= j(
) =¦(a×b)=¦(a)צ(b)= j( 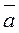 )×j(
)×j( 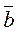 )
)
По условию, ¦ отображает К на К¢. Отсюда следует, что j есть отображение множества К на множество К¢. Отображение j инъективно. В самом деле, из равенства j( 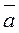 )=j(
)=j( 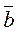 ) следует ¦(a)=¦(b), откуда
) следует ¦(a)=¦(b), откуда 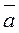 =
= 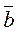 . Следовательно, j является изоморфизмом фактор-кольца к/J на кольцо к¢.
. Следовательно, j является изоморфизмом фактор-кольца к/J на кольцо к¢.
ОПРЕДЕЛЕНИЕ ПОЛЯ
Рассмотрим еще одну алгебраическую структуру и дадим ей несколько эквивалентных определений.
Определение. Пусть (Р,+,×) - кольцо, действие умножения в Р обладает свойством коммутативности и для всяких а,bÎР, а¹0 существует такой xÎР, что а×x=b. Тогда (Р,+,×) называется полем.
Определение. Пусть (Р,+,×) – коммутативное кольцо с единицей и для всякого аÎР, а¹0 существует такой а-1 ÎР, что а×а-1=1. Тогда (Р,+,×) называется полем.
Определение. Алгебру Р=(Р,+,´) будем называть полем, если для элементов множества Р выполняются следующие аксиомы:
А0 (аксиома замкнутости по сложению) "a,bÎР$!cÎР(c=a+b);
А1 (аксиома ассоциативности сложения) "a,b,cÎР(a+(b+c)=(a+b)+c);
А1’ (аксиома коммутативности сложения) "a,bÎР(a+b=b+a);
А2 (аксиома обратимости сложения);
1° $0ÎР"aÎР(a+0=a);
2° "aÎР$-aÎР(a+(-a)=0);
М0 (аксиома замкнутости по умножению) "a,bÎР$!cÎР(c=ab);
М1 (аксиома ассоциативности умножения) "a,b,cÎР(a(bc)=(ab)c);
М1’ (аксиома коммутативности умножения) "a,bÎР(ab=ba);
М2 (аксиома обратимости умножения);
1° $еÎР"aÎР(aе=a);
2° "aÎР$a-1ÎР(aa-1=е);
Д (аксиома дистрибутивности) "a,b,cÎР(a(b+c)=ab+ac ).
Примеры
1. Множество Q является полем
2. Множество Â всех действительных чисел является полем.
Пусть Q 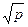 = {a+b
= {a+b 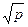 ½a,bÎQ, р - простое число}. Докажем, что Q
½a,bÎQ, р - простое число}. Докажем, что Q 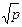 - поле.
- поле.
Определение. Подмножество Р’ поля Р называется подполем поля Р, если относительно операций, определенных в поле Р, множество Р’ само образует поле.
Теорема. Для того, чтобы подмножество Р’ поля Р было подполем поля Р, необходимо и достаточно, чтобы выполнялись следующие условия:
1) "a,bÎP’(a+bÎP’);
2) "a,bÎP’(a-bÎP’);
3) "a,bÎP’(abÎP’);
4) "a,bÎP’(ab-1ÎP’).
Доказать самостоятельно.
Примеры
1. Множество Q является полем, так как сумма, разность, произведение и частное (если делитель отличен от нуля) двух рациональных чисел является рациональным числом.
2. Множество Â всех действительных чисел является полем.
4. Пусть Q 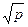 = {a+b
= {a+b 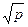 ½a,bÎQ, р -простое число}. Докажем, что Q
½a,bÎQ, р -простое число}. Докажем, что Q 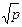 - поле. Пусть a+b
- поле. Пусть a+b 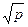 , c+d
, c+d 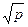 Î Q
Î Q 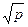 , тогда
, тогда
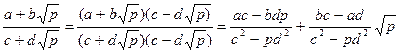 ,
,
но 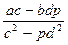 и
и 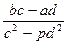 числа рациональные, так как множество рациональных чисел является полем. Таким образом, Q
числа рациональные, так как множество рациональных чисел является полем. Таким образом, Q 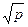 является полем.
является полем.
Упражнения
1. Доказать, что множество ненулевых элементов поля образует группу относительно умножения.
2. В множестве А={а1, а2} заданы действия сложения и умножении таблицами:
| × | а1 | а2 |
| а1 | а1 | а2 |
| а2 | а2 | а1 |
| + | а1 | а2 |
| а1 | а2 | а1 |
| а2 | а1 | а2 |
является ли А кольцом, полем?
3. Доказать, что если Р=(Р,+,×) - поле, то в кольце многочленов P[х] каждый идеал является главным.
4. Доказать, что в любом кольце А имеется нуль, то есть элемент 0 такой, что для всякого аÎА имеет место а+0=а, и для него а×0=0.
5. Кольцо классов вычетов по модулю m является полем тогда и только тогда, когда m - простое число. Доказать.
Дата добавления: 2020-10-25; просмотров: 316;











