ОПРЕДЕЛЕНИЕ ДЛИНЫ СВЕТОВОЙ ВОЛНЫ ПРИ ПОМОЩИ БИПРИЗМЫ ФРЕНЕЛЯ

Интерференцией называется явление взаимодействия двух (или нескольких) волн с одинаковыми периодами, вследствие чего происходит усиление или ослабление амплитуды результирующей волны в разных точках пространства и соответствующее этому перераспределение энергии. Для наблюдения интерференции света необходимо, чтобы взаимодействующие друг с другом волновые процессы были когерентными, то есть, чтобы между ними существовала постоянная разность фаз.

Когерентные световые волны нельзя получить от двух различных источников света, а следует искусственно создать. Существует много методов создания когерентных световых волн, но суть их одна: необходимо разделить волну, излучаемую одним источником, на две части. Если заставить эти две волны пройти разные оптические пути, а потом наложить их друг на друга, будет наблюдаться интерференция. В данной работе для получения когерентных волн используется бипризма.

Бипризма представляет собой две призмы с малыми преломляющими углами α (порядка 30 секунд) сложенные основаниями (рис.1).

Падающий от щели пучок света после преломления в бипризме разделится на два перекрывающихся пучка, как бы исходящих из двух мнимых изображений щели S₁ и S₂ .Так как источники S₁ и S₂ когерентны, то в пространстве за бипризмой будет наблюдаться интерференционная картина, локализованная во всей области пересечения пучков (область АВ на рис. 1).

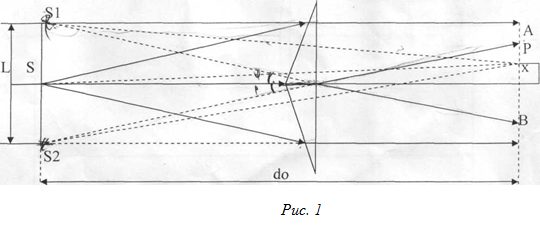Если оптическая разность хода лучей равна целому числу длин волн:

Δ = ± кλ (к=0,1,2,3....) (1)

то разность фаз δ оказывается кратной 2π и колебания, возбуждаемые в точке Р обеими волнами, будут происходить с одинаковой фазой. Следовательно, условие (1) есть условие интерференционного максимума.

Если ∆ равна нечетному числу длин полуволн

Δ = ± (2к + 1) λ/2 (к = 0,1,2...), (2)

то δ = ± ( к2π + π), так что колебания в точке Р находятся в противофазе.

Таким образом, условие (2) есть условие интерференционного минимума.

Пусть S₁ и S₂ (рис.2) – два когерентных источника света, расстояние l, между которыми, мало по сравнению с расстоянием d₀ до экрана.

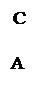
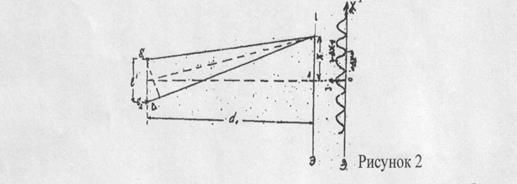
В точке А экрана будет наблюдаться центральная светлая полоса (разность фаз δ = 0).

Определим разность хода ∆, с которой приходят волны в точку С экрана, отстоящую от его середины А на расстоянии x.

При условии, что l и x много меньше d₀ приближенно получим:

,откуда (3)

По условию (1) в точке С будет светлая полоса (максимум нтерференции), если Δ=к λ Тогда расстояние к-ой, светлой полосы от центральной, равное x_к , запишется

x_к=( d₀/ l) · кλ