ОПРЕДЕЛЕНИЕ РАДИУСА КРИВИЗНЫ ЛИНЗЫ С ПОМОЩЬЮ ЯВЛЕНИЯ ИНТЕРФЕРЕНЦИИ

При наложении двух или более световых пучков друг на друга наблюдается усиление света в одних точках пространства и ослабление в других. Это явление называется интерференцией света. Устойчивую интерференционную картину могут давать только когерентные волны, т.е. такие, которые имеют одинаковую частоту и постоянную разность фаз. Для получения контрастной интерференционной картины необходимо также, чтобы их интенсивности были соизмеримы и плоскости колебаний вектора напряженности электрического поля совпадали.

Один из методов получения когерентных волн основан на разделении на две части волны, излучаемой одним источником. Эти волны до попадания в заданную точку пространства проходят различные расстояния (или одинаковые расстояния в средах с различными показателями преломления). Между ними возникает постоянная разность фаз, вследствие чего получается интерференционная картина.

Если разность фаз 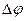в данной точке пространства равна , где m -целое число, то в этом месте происходит усиление колебаний (максимум освещенности), если же разность фаз равна (2m+1)π, то будет наблюдаться ослабление колебаний (минимум освещенности).

Оптическая разность хода ∆ связана с разностью фаз 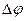соотношением

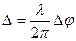. (1)

Зная условия максимумов и минимумов для 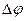, с помощью формулы (1) можно получить условия максимума и минимума для оптической разности хода Δ:

max: 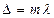(2)

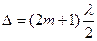min: (3)

где - длина волны интерферирующего света, m = 0, 1, 2, 3 –порядок полосы светлой (темной) полосы интерференции.

Следует отметить, что интерференция будет наблюдаться, если оптическая разность хода не превышает длину когерентности излучения. Длина когерентности есть такая предельная оптическая разность хода, при которой разность фаз при наложении двух волн изменяется не случайно с течением времени. С увеличением номера полосы "m" разность хода растет и при достижении ее величины длины когерентности интерференционная картина исчезает. В качестве примера укажем, что длина когерентности l_к для нелазерных источников света представляет величину порядка 1 мм и меньше. В случае лазерных источников l_к достигает нескольких сантиметров и выше, вплоть до десятков метров.

Интерференционную картину можно получить следующим образом. Если осветить плоско-выпуклую линзу плоской световой волной с большой длиной когерентности ( от лазерного источника), то эта волна частично отразится как от передней выпуклой поверхности, так и от задней плоскости поверхности линзы (рис.1). Две отраженные волны интерферируют друг с другом, и интерференционную картину в виде концентрических темных и светлых колец можно наблюдать на экране. Эти кольца являются примером полос равной толщины. Радиусы колец зависят от радиуса кривизны линзы R и расстояния между линзой и экраном L. Таким образом, измерив радиусы интерференционных колец и расстояние между линзой и экраном, можно определить радиус кривизны линзы. Поскольку диаметр лазерного пучка обычно много меньше размеров линзы, то при выводе рабочей формулы можно использовать приближение параксиальных лучей, т.е. лучей, проходящих вблизи главной оси линзы. В параксиальном приближении интерференционная картина на экране может рассматриваться как результат интерференции двух сферических волн от источников, расположенных в точках S₁ и S₂.

Если оптическая разность хода этих лучей до экрана

l₁ - l₂ = mλ, (4)

то в какой-либо точке на экране будет наблюдаться максимум интерференционной картины, т.е. светлое кольцо.

Опуская вывод формул для определения положения мнимых источников S₁ и S₂. относительно вершины линзы О, запишем выражение для квадрата радиуса 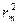светлых колец на экране

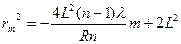(5)

здесь n - коэффициент преломления стекла линзы.

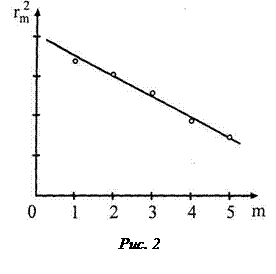
Знак "-" в формуле (5) объясняется тем, что нумерация колец в данной задаче ведется в обратном порядке, т.е. кольцо с минимальным радиусом имеет максимальный номер, соответствующий наибольшей разности хода. Если на экране измерить радиусы колец и построить график зависимо­сти r²(m)=Km , то можно определить радиус R кривизны линзы по угловому коэффициенту К прямой r²(m) (см.рис.2).

Таким образом, радиус кривизны линзы определяется выраже­нием:

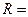
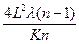(6)

Схема установки представлена на рис.3.

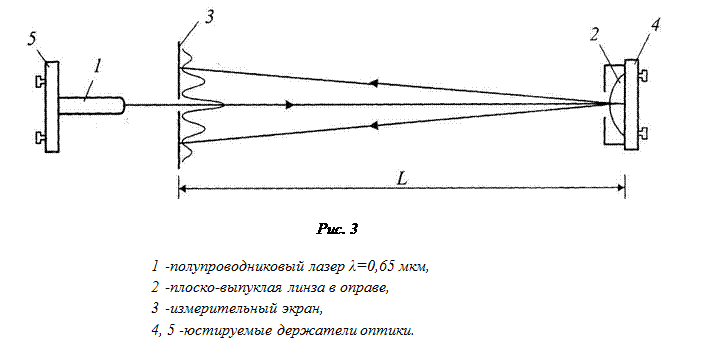
Излучение лазера (1) направляется на линзу (2) со стороны выпуклой поверхности. Для получения контрастной интерференционной картины на обе поверхности линзы нанесено отражающее покрытие Al. Коэффициент отражения от выпуклой поверхности линзы составляет 20% , от плоской поверхности - 100%. Стекло К-8, из которого изготовлена линза, имеет показатель преломления n = 1,52. Длина когерентности l_к излучения используемого лазера больше двух максимальных толщин линзы (в данном случае l_к=20 мм). Для увеличения эффективной длины L>>d свет в установке распространяется по маршруту лазер-линза-экран.

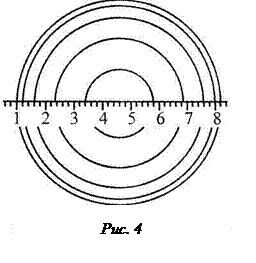На экране нанесена координатная сетка, с помощью которой можно измерить диаметры (радиусы) светлых интерферен­ционных колец (рис.4).