Дисперсия суммы коррелированных и некоррелированных погрешностей

Согласно теории вероятностей дисперсии суммы двух величин в общем случае [10]

D(x+y)=D(x)+D(y)+2k_xy, (2.46)

где D(x) – дисперсия x; D(y) – дисперсия y; k_xy=ρ σ(x)×σ(y) – их взаимный корреляционный момент (ρ – коэффициент корреляции). Отсюда среднее квадратическое значение σ_Σ отклонения суммы этих величин от ее математического ожидания

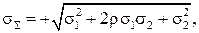(2.47)

Если эти величины между собой некоррелированы, то ρ=0 и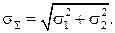

Однако если x и y жестко и положительно коррелированы между собой (ρ=+1), т. е. Δy принимает значения, лишь строго пропорциональные Δx, то всякое положительное отклонение +Δx сопровождается также положительным отклонением +Δy и отклонение Δ(x+y) определяется как Δx+Δy. Это формально следует и из формулы для σ_Σ при ρ=+1, ибо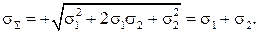

Если же при возрастании x значения y, наоборот, линейно убывают, то ρ= -1 и

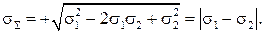(2.48)

Таким образом, оценки жестко коррелированных погрешностей (ρ=±1) должны суммироваться не геометрически, а алгебраически с учетом их знаков, т. е. складывается, когда их знаки совпадают, и вычитаются, когда их знаки оказываются противоположными.

Это правило теории вероятностей в совершенно равной степени относится как к чисто случайным погрешностям, так и к систематическим погрешностям, возникающим от случайного изменения влияющих факторов. Так, например, погрешности измерительных преобразователей зависят от изменений температуры окружающей среды и это влияние хорошо воспроизводится от опыта к опыту и поэтому обычно классифицируются как систематические. Однако при суммировании температурных погрешностей ряда преобразователей они могут оказаться как коррелированными, так и некоррелированными между собой и складываться как алгебраически, так и геометрически.

Практические правила определения результирующей погрешности сложных измерительных устройств

1. Для определения значения оценки результирующей погрешности всего измерительного устройства должны учитываться взаимные корреляционные связи различных составляющих погрешности отдельных преобразователей, поэтому исходными данными для более точного расчета должны служить значения соответствующих оценок именно отдельных составляющих, а не значение оценки суммарных погрешностей преобразователей.

Эти составляющие, прежде всего, разделяются на аддитивные и мультипликативные для их последующего раздельного суммирования.

2. Так как суммировать с учетом корреляционных связей можно лишь средние квадратические значения составляющих, то для каждой составляющей должны быть по исходным данным найдены ее средние квадратические значения.

3. Далее должны быть выделены группы сильно коррелированных между собой составляющих погрешности и внутри этих групп произведено алгебраическое суммирование. К ним, как правило, относят погрешности, вызванные одной общей причиной (общий источник питания, примерно одинаковые изменения температуры и т. д.), когда тесные корреляционные связи определяются логически, и для них принимают ρ равным +1 или –1. Погрешности же, между которыми такие взаимосвязи не обнаруживаются, относят к некоррелированным и для них принимают ρ=0.

4. После того как все группы сильно коррелированных погрешностей выделены и внутри их произведено алгебраическое суммирование, суммарные по группам и оставшиеся вне группы погрешности можно считать уже некоррелированными и складывать по правилу σ_Σ²=Σ σ_i².

Таким образом, находятся лишь средние квадратические значения аддитивной и мультипликативной составляющих результирующей погрешности, которые не учитывают деформации законов распределения при образовании композиций, и остаются неизвестными параметры формы закона распределения результирующей погрешности.