Нахождение рациональных корней многочленов с целыми коэффициентами
Следствие 1 из основной теоремы алгебры утверждает, что всякий многочлен, заданный над полем С, имеет в этом поле сколько корней, какова его степень. Существуют различные методы нахождения корней многочлена. Так, корни многочленов второй, третьей или четвертой степени можно найти, решив соответственно квадратное, кубическое или уравнение четвертой степени. Для решения уравнений высших степеней используются приближенные методы, однако иногда можно найти корни уравнения с целыми коэффициентами точно, а не приближенно. Рассмотрим один из способов, который позволяет найти рациональные корни многочлена с целыми коэффициентами, если таковые имеются.
Теорема 1. Если несократимая дробь 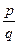 (pÎZ,qÎN) является корнем многочлена f(x)=anxn+an-1xn-1+…+a1x+a0ÎZ[x], тогда p½a0 , а q½an.
(pÎZ,qÎN) является корнем многочлена f(x)=anxn+an-1xn-1+…+a1x+a0ÎZ[x], тогда p½a0 , а q½an.
Доказательство. Так как 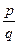 является корнем многочлена f(x), то
является корнем многочлена f(x), то
f( 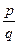 )=an(
)=an( 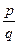 )n+an-1(
)n+an-1( 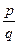 )n-1+…+a1
)n-1+…+a1 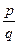 +a0=0.
+a0=0.
Умножим обе части этого равенства на qn, получим
anpn+an-1pn-1q+an-2pn-2q2+…+a1pqn-1+a0qn=0 (*)
(*) Û anpn = -(an-1pn-1q+an-2pn-2q2+…+a1pqn-1+a0qn)
Из этого равенства получаем p½(an-1pn-1q+an-2pn-2q2+…+a1pqn-1+a0qn), следовательно, p½a0qn. Но дробь 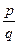 несократимая, то есть (p,q)=1, тогда (p,qn)=1, тогда p½a0. Аналогично докажем второе утверждение. Для этого снова обратимся к равенству (*) и перейдем к равносильному равенству
несократимая, то есть (p,q)=1, тогда (p,qn)=1, тогда p½a0. Аналогично докажем второе утверждение. Для этого снова обратимся к равенству (*) и перейдем к равносильному равенству
(*) Û a0qn=-(anpn+an-1pn-1q+an-2pn-2q2+…+a1pqn-1).
Из этого равенства получаем q½(anpn+an-1pn-1q+an-2pn-2q2+…+a1pqn-1), следовательно, q½anpn. Но дробь 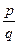 несократимая, то есть (p,q)=1, тогда (pn,q)=1, тогда q½an. Теорема доказана.
несократимая, то есть (p,q)=1, тогда (pn,q)=1, тогда q½an. Теорема доказана.
Следствие 1. Если многочлен f(x) с целыми коэффициентами имеет целый корень, то он является делителем свободного члена.
Доказательство - в качестве упражнения.
Следствие 2. Среди рациональных корней многочлена с целыми коэффициентами f(x)=xn+an-1xn-1+…+a1x+a0 могут быть только целые числа.
Доказательство - в качестве упражнения.
Теорема 2. Если несократимая дробь 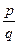 (pÎZ,qÎN) является корнем многочлена f(x)=anxn+an-1xn-1+…+a1x+a0ÎZ[x], тогда "kÎZ (p-kq¹0Þ(p-kq)½f(k)).
(pÎZ,qÎN) является корнем многочлена f(x)=anxn+an-1xn-1+…+a1x+a0ÎZ[x], тогда "kÎZ (p-kq¹0Þ(p-kq)½f(k)).
Доказательство. предположим противное. пусть условие теоремы выполнено, а $ kÎZ (p-kq)¹0, и f(k) не делится на (p-kq). Разделим многочлен f(x) на двучлен (х- k), по теореме Безу f(x)=(х-k)q(x)+f(k), q(x)=bn-1xn-1+…+b1x+b0, тогда f( 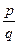 )=(
)=( 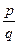 -k)(bn-1(
-k)(bn-1( 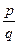 )n-1+…+b1
)n-1+…+b1 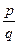 +b0) +f(k)=0. Умножив последнее равенство на qn, получим (p-kq)(bn-1pn-1+...+b1pqn-2+b0qn-1)+f(k)=0. это равносильно (p-kq)( bn-1pn-1+...+ b1pqn-2+ b0qn-1)=-f(k)Þ(p-kq)½f(k)), что противоречит предположению. Теорема доказана.
+b0) +f(k)=0. Умножив последнее равенство на qn, получим (p-kq)(bn-1pn-1+...+b1pqn-2+b0qn-1)+f(k)=0. это равносильно (p-kq)( bn-1pn-1+...+ b1pqn-2+ b0qn-1)=-f(k)Þ(p-kq)½f(k)), что противоречит предположению. Теорема доказана.
Следствие 1. Если многочлен f(x) с целыми коэффициентами имеет целый корень a, то (a-1)½f(1) и (a+1)½f(-1).
Доказательство - в качестве упражнения.
Следствие 2. Если несократимая дробь 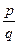 (pÎZ,qÎN) является корнем многочлена f(x) с целыми коэффициентами, тогда (p-q)½f(1) и (p+q)½f(-1).
(pÎZ,qÎN) является корнем многочлена f(x) с целыми коэффициентами, тогда (p-q)½f(1) и (p+q)½f(-1).
Доказательство - в качестве упражнения.
Замечание. На двух доказанных теоремах основан алгоритм нахождения рациональных корней многочленов с целыми коэффициентами:
1) найти все делители свободного члена a0 (как положительные, так и отрицательные);
2) найти все делители старшего коэффициента an (только положительные);
3) составить всевозможные дроби, разделив числа из п.1 на числа из п.2;
4) найти f(1) и f(-1). Если хотя бы одно из них, например х=1 равно нулю, тогда это число – корень многочлена. В этом случае делим f(x) на (х-1) и для частного повторяем алгоритм сначала. Иначе
5) вычеркнуть из полученных в п.3 те числа, которые не удовлетворяют хотя бы одному из условий (p-q)½f(1) и (p+q)½f(-1);
6) проверить по схеме Горнера, будут ли корнями оставшиеся после вычеркивания числа.
Пример. Найти рациональные корни многочлена f(x)=2x3-2x2-x-6.
Делители свободного члена: ±1, ±2, ±3, ±6;
делители старшего коэффициента: 1, 2;
на основании теоремы 1 получим числа, которые могут быть корнями данного многочлена: ±1, ±2, ±3, ±6, 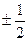 ,
, 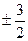 ;
;
f(1)=2-2-1-6=-7, f(-1)=-2-2+1-6=-9;
проверим, какие из чисел ±2, ±3, ±6, 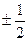 ,
, 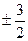 удовлетворяют второй теореме.
удовлетворяют второй теореме.
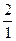
| - 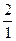
| 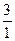
| - 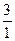
| 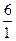
| - 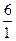
| 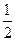
| 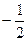
| 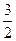
| - 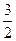
| |
| (p-q)½(-7) | + | - | - | - | - | + | + | - | + | - |
| (p+q)½(-9) | + | - | + | - |
после применения теоремы 2 у нас осталось два числа, которые могут быть корнями данного многочлена х=2 и х= 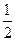 .
.
делим по схеме Горнера f(x) на (х-2) и (х- 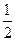 ).
).
| -2 | -1 | -6 | ||
| х=2 | ||||
х= 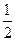 ; ;
| 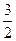 +3¹0 +3¹0
|
Таким образом, х=2 – единственный рациональный корень многочлена f(x)=2x3-2x2-x-6.
Дата добавления: 2020-10-25; просмотров: 1009;











