Основная теорема алгебры

Если рассматривать поле рациональных чисел, то увидим, что далеко не всякий многочлен, заданный над этим полем, имеет рациональные корни. Например, многочлен f(х) = х² - 3 не имеет рациональных корней. То же можно сказать и о многочленах, заданных над полем действительных чисел. В этом поле, например, многочлен f(х)=х²+1 не имеет действительных корней. Самым «обширным» числовым полем является поле комплексных чисел. В этом поле извлекается корень n-й степени из любого комплексного числа. О корнях многочленов, заданных над полем комплексных чисел, можно сказать следующее:

Основная теорема алгебры (теорема о существовании корня). Всякий многочлен f(x), заданный над полем комплексных чисел, степени n ³ 1 имеет, по меньшей мере, один комплексный корень.

Еще в 1629 г. французский ученый Жирар предположил, что любое алгебраическое уравнение n-й степени имеет n корней, действительных и мнимых. В 1746 г. французский ученый Д’аламбер впервые попытался доказать основную теорему алгебры, но его рассуждения оказались нестрогими. В 1799 г. Гауссу удалось получить сравнительно удовлетворительное доказательство. Впоследствии Гаусс нашел еще несколько доказательств основной теоремы.

Так как основная теорема алгебры тесно связана с понятием непрерывности, то она не является чисто алгебраической теоремой.

Здесь будет дано доказательство этой теоремы, в котором многочлен с комплексными коэффициентами рассматривается как комплексная функция комплексного аргумента.

Обычное определение непрерывной функции, рассматриваемое в курсе математического анализа, без особых затруднений можно перенести и на тот случай, когда переменное х и функция f(x) принимают комплексные значения. Приходится лишь вместо абсолютной величины говорить о модуле, а именно: комплексная функция f(x) комплексного переменного х называется непрерывной в точке х_о, если для всякого наперед заданного положительного числа e можно указать такое положительное число d, что для всякого значения х, удовлетворяющего неравенству

|х- х₀| < d, (1)

будет иметь место неравенство

|f(x)-f(x₀)|<e (2)

для соответствующих значений функций. Здесь две вертикальные черточки означают уже не абсолютную величину, а модуль комплексного числа.

Так как х и f(х) принимают комплексные значения, то можно положить, что x=x+ ih и w =f(х)=u+iv. Возьмем, далее, для изображения значений переменного х и функции f(x) две плоскости Р и Q, причем на плоскости Р возьмем прямоугольную систему координат xОh, а на плоскости Q - прямоугольную систему координат uO’v. Каждое значение x=x+ ih комплексного переменного можно изобразить точкой на плоскости P с координатами. (x,h) (или вектором, исходящим из начала O и имеющим конец в этой точке). Соответствующее значение функции w=f(х)=u+iv будет изображаться точкой w на плоскости Q с координатами (u,v). Будем плоскость Р называть плоскостью переменного х, a Q — плоскостью функции f(х).

Возьмем теперь на плоскости Р переменного х круг С некоторого радиуса с центром в некоторой точке плоскости Р. Под замкнутым кругом С мы будем подразумевать все точки этого круга, включая и его границы.

Функция f(x) комплексного переменного называется непрерывной в замкнутом круге С, если она непрерывна в каждой точке этого круга (включая, следовательно, и его границы). В случае, когда функция f(х) непрерывна в любой точке х_о плоскости переменного х, функция f(x) называется непрерывной во всей плоскости. В этом случае мы будем говорить, что f(x) непрерывна, для краткости опуская слова «во всей плоскости»

Обратимся теперь к многочлену f(х) над полем комплексных чисел, т.е. многочлену с комплексными коэффициентами. Если его рассматривать как комплексную функцию комплексного переменного х, то можно доказать следующее

предложение.Многочлен f(x) есть непрерывная функция комплексного переменного х.

Доказательство. Совершенно так же, как в курсе математического анализа, обнаруживается, что сумма и произведение нескольких непрерывных комплексных функций комплексного аргумента х также непрерывны. Отсюда получается, что целая неотрицательная степень х^k и произведение a_kx^k постоянной a_k на степень x^k непрерывны, так как, очевидно, х и постоянная a_k являются непрерывными комплексными функциями комплексного аргумента х. Следовательно, сумма членов a_kx^k (k=0,…,n), то есть многочлен

f(х)=a_nxⁿ+a_n-1x^n-1+…+a₁x+a₀

есть непрерывная комплексная функция комплексного аргумента х.

из этой теоремы легко получается, что модуль |f(x)| также непрерывная функция комплексного переменного х. В самом деле, согласно свойству модуля

||f(x)-f(x₀)||£|f(x)-f(x₀)|. (3)

Но по доказанной теореме о непрерывности многочлена f (x) можно для всякого e> 0 указать такое d> 0, что при |x — х₀|<d будет иметь мести неравенство |f(x)-f(x₀)|<e. Отсюда благодаря неравенству (3) и подавно будет:

||f(x)-f(x₀)||<e при |x — х₀|<d.

Для доказательства основной теоремы алгебры нам понадобится еще несколько лемм и теорем.

Лемма 1 (о многочлене без свободного члена). Для всякого многочлена f(х) a_nxⁿ+a_n-1x^n-1+…+a₁x+a₀ степени n ³1 со свободным членом а₀, равным нулю, можно для любого e> 0 указать такое d> 0, что для всех х, удовлетворяющих неравенству |х|< d, будет иметь место неравенство |f(x)|<e (т. е. при достаточно малых по модулю значениях х рассматриваемый многочлен f(x) может быть сделан по модулю сколь угодно малым).

Доказательство. Возьмем в качестве x₀ значение 0. Многочлен f(х) есть непрерывная функция комплексного переменного x, следовательно, для любого e> 0 можно указать такое d> 0, что при всех х, удовлетворяющих неравенству |х-0|<d, будет |f(x)—f(0)|<e или при |х|< d будет |f(x)|<e, так как, очевидно, f(0) =0. .

Теорема 1 (о модуле старшего члена). Пусть

f(х)=a_nxⁿ+a_n-1x^n-1+…+a₁x+a₀ - многочлен степени n ³1 и А - наибольшая из величин модулей |а_n-1|, |а_n-2|,…, |а₀|. Тогда для любого наперед заданного действительного положительного числа k будет выполняться неравенство

|a_nxⁿ|>k|a_n-1x^n-1+…+a₀|

при |x|> .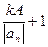

Эта теорема понадобится также в дальнейшем.

Доказательство. Усиливаем очевидное неравенство

|a_n-1x^n-1+…+a₀|£|a_n-1||x|^n-1+…+|a₀|,

заменяя в его правой части |а_n-1|, |а_n-2|,…, |а₀| величиной А:

|a_n-1x^n-1+…+a₀|£А(|x|^n-1+|х|^n-2+…+1),

или, суммируя геометрическую прогрессию,

|a_n-1x^n-1+…+a₀|£А .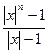

Если взять x>1, то последнее неравенство можно усилить следующим образом:

|a_n-1x^n-1+…+a₀|£А .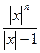

Выясним, для каких значений х

kА 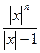<|a_nxⁿ|,

для чего решаем это неравенство:

kА 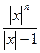<|a_n ||x|ⁿ , kА 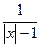<|a_n|,

откуда |х|> .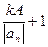

Итак, при |х|> 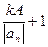, будет |a_nxⁿ|>k|a_n-1x^n-1+…+a₀|, что и требовалось доказать.

На основании теоремы 1 легко получается следующая лемма.

Лемма 2 (о возрастании модуля многочлена). Модуль всякого многочлена f(х) степени n³1 при достаточно больших значениях |х| будет больше любого наперед заданного действительного положительного числа М.

Доказательство. Так как модуль суммы больше или равен разности модулей, то

|f(х)| ³|a_nxⁿ|-|a_n-1x^n-1+…+a₀|. (4)

Применив теорему 1, полагая, k = 2 и |х|> 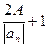, получим:

|a_n-1x^n-1+…+a₀|< 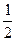|a_nxⁿ|

Таким образом, заменяя в правой части неравенства (4) вычитаемое большей величиной — 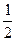|a_nxⁿ|, мы неравенство только усиливаем:

|f(х)|> |a_nxⁿ|- 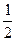|a_nxⁿ|= 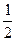|a_nxⁿ|.

Возьмем теперь х таким большим по модулю, чтобы одновременно

|х|> 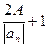и |х|> .

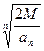Тогда при таких значениях х

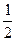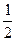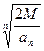|f(х)|> |a_nxⁿ|> |a_n|( )ⁿ,

после соответствующих сокращений: |f(х)|>М, что и требовалось показать.

Мы подошли к лемме, играющей решающую роль в доказательстве основной теоремы алгебры.

Лемма Даламбера. Если многочлен f(х)=a_nxⁿ+a_n-1x^n-1+…+a₁x+a₀¹0, степени n³1 не обращается в нуль при х=х₀,то всегда можно подобрать комплексное число h ¹0, чтобы |f(х₀ + h)|<|f(х₀)| (при этом h может быть даже сколь угодно малым по модулю).

Доказательство. Разложим f(х₀ + h) по степеням h:

f(х₀ + h)= f(х₀)+hf’(x₀)+…+hⁿ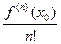

или

f(х₀ + h)= f(х₀)+g(h),

где

g(h)= hf’(x₀)+…+hⁿ .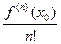

очевидно, что g(h) ¹0, так как 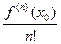=a_n¹0. Пусть c_mh^m - отличный от нуля член наименьшей степени многочлена g(h) (1£m£n). Тогда мы можем написать, что

g(h)= c_mh^m(1+k(h)),

где k(h)¹0 при m<n и k(h)=0 при m=n. Таким образом,

f(х₀+h)=f(х₀)+c_mh^m(1+k(h)),

или

f(х₀+h)= (f(х₀)+c_mh^m )+ c_mh^m k(h).

Так как модуль суммы меньше или равен сумме модулей, а модуль произведения равен произведению модулей, то отсюда получаем неравенство:

|f(х₀+h)|£|f (х₀)+c_mh^m |+|c_mh^m ||k(h)|. (5)

Но k(h) есть многочлен без свободного члена. Следовательно, по лемме 1 можно для e=1 подобрать такое d₁>0, чтобы в случае |h|<d₁ выполнялось условие |k(h)| <1. Усиливаем при |h|<d неравенство (5) следующим образом:

|f(х₀+h)| <|f(х₀)+c_mh^m |+|c_mh^m |.

Теперь подберем аргумент h так, чтобы аргумент c_mh^m отличался от аргумента f(х₀) на p:

arg(c_mh^m)=j+p,

где j - аргумент f(х₀). Так как arg (c_mh^m)= arg c_m +m arg h, то получаем уравнение: arg c_m +m arg h=j+p, из которого находим без труда, что

arg h= 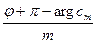=w.

С этого момента будем предполагать, что arg h=w. При таком предположении вектор 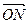, изображающий c_mh^m, лежит на одной прямой с вектором 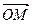, изображающим f(х₀), но направлен в противоположную сторону, в силу чего

|f(х₀)+c_mh^m |=|f(х₀)|- |c_mh^m | и

|f(х₀+h)| <||f(х₀)|- |c_mh^m ||+|c_mh^m |. (6)

Найдем, при каких значениях h будут одновременно выполняться неравенство (6) и неравенство

|c_mh^m | <|f(х₀)|. (7)

Решаем неравенство (7) относительно h:

|c_mh^m |=|c_m||h|^m <|f(х₀)|, откуда

|h|< 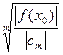=d₂

(корень m-й степени, очевидно, следует брать в арифметическом смысле).

Обозначим теперь через d наименьшее из чисел d₁ и d₂. Тогда при |h|<d и argh=w будут одновременно выполняться неравенства (6) и (7). Но из неравенства (7) следует, что разность |f(х₀)|-|c_mh^m| - положительное действительное число, а потому

||f(х₀)|- |c_mh^m ||=|f(х₀)|-|c_mh^m|.

Таким образом, предполагая |h| <d и argh=w , мы можем неравенство (6) преобразовать в

|f(х₀+h)| <|f(х₀)|- |c_mh^m |+|c_mh^m |,

или после уничтожения подобных членов,

|f(х₀+h)| <|f(х₀)|.

Лемма Даламбера доказана.

Кроме леммы Даламбера, существенное значение в доказательстве основной теоремы будет иметь следующая теорема, относящаяся к действительной функции комплексного переменного, то есть к функции, принимающей только действительные значения при всевозможных комплексных значениях х.

Действительная функция j(х) комплексного переменного х, непрерывная в некотором замкнутом круге С, достигает в этом замкнутом круге своего наименьшего значения, то есть в замкнутом круге С существует такая точка х₀, что j(х₀)£j(х) для всех точек х замкнутого круга С. (Кроме того, функция j(х) достигает в замкнутом круге С и своего наибольшего значения, но в данном случае это обстоятельство не представляет интереса.)

Мы не приводим доказательство, так как оно относится к теории функций комплексного переменного.

Посмотрим, что дает эта теорема для модуля многочлена f(х), являющегося, очевидно, действительной функцией комплексного переменного.

Для большей наглядности мы воспользуемся геометрической иллюстрацией. Восставим в каждой точке плоскости переменного х перпендикуляр с длиной, равной (при заданной единице масштаба) модулю значения многочлена f(х) в точке х. В силу непрерывности модуля многочлена концы перпендикуляров должны образовать некоторую непрерывную поверхность, расположенную над плоскостью переменного х. Возьмем теперь в качестве замкнутого круга С круг на плоскости переменного х с центром в точке О и с произвольным радиусом R. Этому замкнутому кругу С будет соответствовать кусок поверхности.

Так как модуль |f(х)| многочлена f(х) удовлетворяет условиям теоремы, то среди точек замкнутого круга С найдется по меньшей мере одна такая точка х₀, для которой перпендикуляр будет иметь наименьшую длину |f(х₀)|, т. е.

|f(х₀)|£ |f(х)| (8)

для всех точек х замкнутого круга С. Эту точку х₀ мы, назовем точкой минимума |f(х)| в замкнутом круге С.

Мы утверждаем, что при соответствующем выборе радиуса R неравенство (8) будет иметь место уже для точек всей плоскости переменного х, то есть х₀ при соответствующем выборе радиуса R будет точкой минимума |f(х)| на всей плоскости переменного х.

В самом деле, пусть f(х) - многочлен степени n³1. Тогда согласно лемме 2 о возрастании модуля многочлена можно указать такое N > 0, что при |х|>N выполняется |f(х)|>|f(0)|. Возьмем теперь радиус R круга С равным N. Пусть х₀ - точка минимума |f(x)| в замкнутом круге С радиуса N. Тогда для всех точек х этого замкнутого круга будет справедливо неравенство (8); в частности, будет иметь место

|f(х₀)|£ |f(0)|.

Но неравенство (8) будет выполняться и для всех точек х, лежащих вне рассматриваемого круга, так как если |х|> N, то

|f(х) >|f(0)| ³|f(х₀)|.

Теперь мы можем приступить к доказательству теоремы.

Доказательство. Покажем, что упомянутая выше точка х₀ минимума модуля многочлена f(х) на всей плоскости переменного х является корнем f(х). Допустим противное: пусть х₀ не является корнем многочлена f(х). Тогда f(х₀)¹0, и мы можем применить лемму Даламбера. Согласно этой лемме можно указать такое комплексное число h, что

|f(х₀+h)| <|f(х₀)|.

или, обозначив х₀+h=х₁, получим |f(х₁)| <|f(х₀)|. Но последнее неравенство противоречит тому, что х₀ является точкой минимума |f(х)| на всей плоскости х. Следовательно, наше допущение неверно, и f(х₀)=0.

В курсе алгебры нам гораздо интереснее, чем доказательство самой теоремы, ее следствия. Рассмотрим наиболее важные из них.

Следствие 1. Всякий многочлен f(x)ÎC[x], deg f(x)³2 приводим над полем комплексных чисел.

Доказательство. Действительно, по основной теореме алгебры всякий многочлен f(x)ÎC[x], deg f(x)³1 имеет в поле С корень a, тогда по следствию из теоремы Безу f(x)=(х-a)g(x) и deg g(x)³1, следовательно, f(x) приводим над полем комплексных чисел. Обратно, пусть р(х) – неприводим над полем комплексных чисел. Но основной теореме алгебры всякий многочлен р(x)ÎC[x], deg р(x)³1 имеет в поле С корень a₀, следовательно, р(x)=(х-a)g(x), а так как р(х) – неприводим, то g(x)=с и р(x)=(х-a)с, то есть неприводимы над полем С только многочлены первой степени.

Следствие 2. Всякий многочлен f(x)=a_nxⁿ+a_n-1x^n-1+…+a₁x+a₀ степени n³1 имеет в поле С ровно n корней, если считать каждый корень столько раз, какова его кратность.

Доказательство. Докажем методом математической индукции по степени многочлена n.

Если n=1, то f(x)=ax+b, a,b,xÎC. Так как в поле С уравнение ax+b=0 однозначно разрешимо, то многочлен f(x) имеет в этом поле единственный корень, то есть теорема верна.

Предположим, что теорема верна для любого многочлена степени меньшей n, и рассмотрим многочлен n-ой степени f(x). по основной теореме алгебры всякий многочлен f(x)ÎC[x], deg f(x)³1 имеет в поле С корень a, тогда по следствию из теоремы Безу f(x)=(х-a)g(x) и deg g(x)=n-1. Так как deg g(x)<n, то для него справедливо индуктивное предположение, то есть многочлен g(x) имеет ровно n-1 корень с учетом их кратности. Пусть b - произвольный корень многочлена g(x) (b¹a), то есть g(b)=0, тогда f(b)=(b-a)g(b)Ûf(b)=0Û b - корень многочлена f(x). Обратно, если b - произвольный корень многочлена f(x), отличный от a (b¹a), то f(x)=(х-a)g(x)Þ f(b)=(b-a)g(b)=0, а так как в поле нет делителей нуля и (b-a)¹0, то g(b)=0Ûb - корень многочлена g(x). Таким образом, мы доказали, что всякий корень многочлена g(x) является корнем многочлена f(x), а любой, может быть за исключением a , корень многочлена f(x) является корнем многочлена g(x). Можно сделать вывод, что многочлен f(x) имеет (n-1)+1=n корней, то есть теорема верна, следовательно, она верна для любого натурального числа n.

Следствие 3. Если многочлен f(x)=a_nxⁿ+a_n-1x^n-1+…+a₁x+a₀, степени n³1 имеет в поле С различные корни a₁, a₂, …, a_s кратности соответственно k₁,k₂,…,k_s, то

f(х) =a_n(х—a₁)^k1(x—a₂)^k2...(x—a_s)^ks,

и это разложение является для многочлена f(х) единственным с точностью до порядка следования сомножителей в силу единственности разложения многочлена на неприводимые множители.

Следствие 4. Пользуясь разложением многочлена на линейные множители, можно получить так называемые формулы Виета. А именно, пусть

f(x)=xⁿ+a_n-1x^n-1+…+a₁x+a₀ - какой-нибудь многочлен, n³1, с комплексными коэффициентами и со старшим коэффициентом, равным единице. Обозначим его корни через a₁, a₂, …, a_n. Тогда можно написать следующее разложение многочлена f(x) на линейные множители:

xⁿ+a_n-1x^n-1+…+a₁x+a₀=(х—a₁)(x—a₂)...(x—a _n ).

Перемножая линейные множители, получаем

xⁿ+a_n-1x^n-1+…+a₁x+a₀= xⁿ -(a₁+a₂+…+a_n)x^n-1+…+(-1) ⁿa₁a₂…a_n.

Но если два многочлена равны, то их коэффициенты при одинаковых степенях х должны совпадать. Следовательно,

a_n-1=-(a₁+a₂+…+a_n)

a_n-2=a₁a₂+a₁a₃+…+a _n-1a_n

……………………………… (*)

a₀=(-1) ⁿa₁a₂…a_n.

В правых частях соотношений (*) стоят всевозможные произведения корней по одному, по два, по три и т. д. Мы пришли к формулам Виета, выражающим коэффициенты многочлена f(x) через его корни.

Формулы Виета для многочлена f(x)=a_nxⁿ+a_n-1x^n-1+…+a₁x+a₀ , очевидно, имеют вид:

a₁+a₂+…+a_n=-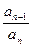

a₁a₂+a₁a₃+…+a _n-1a_n=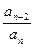

………………………..

a₁a₂…a_n=(-1) ⁿ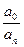

Пример. Найти многочлен четвертой степени со старшим коэффициентом 2, имеющий 1 и - 1 простыми корнями и 5 - двукратным корнем.

Записываем искомый многочлен в виде f(х) =2(x⁴+ax³+bx²+cx+d). По формулам Виета находим, что

a=-(1+5+5-1)=-10,

b=1*(-1)+1*5+5*(-1)+1*5+5*(-1)+5*5=-24,

c=1*(-1)*5+1*5*5+(-1)*5*5+1*(-1)*5=-10,

d=-1*1*5*5=-25.

Следовательно, f(х) =2(x⁴-10x³-24x²-10x-25) =2x⁴-20x³-48x²-20x-50.