МНОГОЧЛЕНЫ НАД ПОЛЕМ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ
Обращаясь к многочленам с действительными коэффициентами, можно вывести еще несколько свойств, связанных с основной теоремой алгебры. Но для этого вспомним свойства комплексно сопряженных чисел.
a=a+bi,  =a-bi,
=a-bi,
a+  =2aÎÂ,
=2aÎÂ,
a  =a2+b2ÎÂ,
=a2+b2ÎÂ,
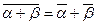 ,
,

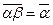
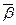 ,
,
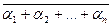 =
= 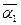
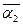 ….
…. 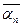 ,
,
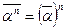 .
.
Если сÎÂ, то 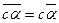 .
.
Теперь рассмотрим следующие свойства многочленов с действительными коэффициентами.
Следствие 5. Комплексные корни многочлена f(x)=anxn+an-1xn-1+…+a1x +a0 степени n³1 с действительными коэффициентами попарно сопряжены, то есть если a - комплексный корень f(x), то и сопряженное число  также корень f(x).
также корень f(x).
Доказательство. Так как a - корень многочлена f(x), тогда
f(a)=anan+an-1an-1+…+a1a+a0 =0.
Отсюда в силу равенства свойств комплексно сопряженных чисел получим
f(  )=an
)=an  n+an-1
n+an-1  n-1+…+a1
n-1+…+a1  +a0 =
+a0 = 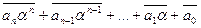 =
=
= 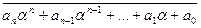 =
= 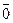 =0,
=0,
то есть f(  )=0, и мы видим, что
)=0, и мы видим, что  также корень f(x).
также корень f(x).
Следствие 6. Комплексно сопряженные корни многочлена f(x)=anxn+an-1xn-1+…+a1x+a0, степени n³1 с действительными коэффициентами имеют одинаковую кратность, т. е. если a - комплексный корень f(x) кратности k, то и число  также корень f(x) кратности k.
также корень f(x) кратности k.
Доказательство. Докажем данное утверждение методом от противного. Пусть a - комплексный корень f(x) кратности k, тогда по следствию 4  также является корнем многочлена f(x). Предположим, что корень
также является корнем многочлена f(x). Предположим, что корень  имеет кратность m и m¹k, не нарушая общности доказательства, можем считать, что m>k. По определению кратного корня имеем
имеет кратность m и m¹k, не нарушая общности доказательства, можем считать, что m>k. По определению кратного корня имеем
 (x-a)k½f(x)Ù (x-a)k+1½ f(x) Ù (x-
(x-a)k½f(x)Ù (x-a)k+1½ f(x) Ù (x-  )m½f(x)Ù (x-
)m½f(x)Ù (x-  )k+1½f(x), то есть
)k+1½f(x), то есть
f(x)=(x-a)k(x-  )mg(x), где g(x) – многочлен степени n-m-k, не имеющий корней a и
)mg(x), где g(x) – многочлен степени n-m-k, не имеющий корней a и  , тогда f(x)=(x-a)k(x-
, тогда f(x)=(x-a)k(x-  )mg(x)=((x-a)(x-
)mg(x)=((x-a)(x-  ))k(x-
))k(x-  ) m-k g(x)=
) m-k g(x)=
=(x2-(a+  )x+a
)x+a  )k(x-
)k(x-  ) m-k g(x)=(x2+px+q)ky(x), где -(a+
) m-k g(x)=(x2+px+q)ky(x), где -(a+  )=pÎÂ, a
)=pÎÂ, a  =qÎÂ,
=qÎÂ,
(x-  ) m-k g(x)=y(x). По теореме о делении с остатком y(x)ÎÂ[x], но
) m-k g(x)=y(x). По теореме о делении с остатком y(x)ÎÂ[x], но
y(x)= (x-  ) m-k g(x), то есть
) m-k g(x), то есть  - корень y(x)ÎÂ[x], а тогда по следствию 4 a также корень y(x), то есть корень a имеет кратность большую k, что противоречит условию. полученное противоречие доказывает наше утверждение.
- корень y(x)ÎÂ[x], а тогда по следствию 4 a также корень y(x), то есть корень a имеет кратность большую k, что противоречит условию. полученное противоречие доказывает наше утверждение.
Следствие 7. Всякий многочлен с действительными коэффициентами степени n³3 приводим над полем действительных чисел.
Доказательство. Действительно, многочлен f(x) по основной теореме алгебры обязательно имеет корень a. Если a действительное число, тогда по следствию из теоремы Безу f(x)=(x-a)g(x), где deg g(x)³2, то есть f(x) приводим над полем Â. Если a=a+bi - комплексное число, тогда по следствию 5,  =a-bi также корень многочлена f(x), тогда по следствию из теоремы Безу
=a-bi также корень многочлена f(x), тогда по следствию из теоремы Безу
f(x)=(x-a)(x-  )g1(x)=(x2+px+q)g1(x), причем (x2+px+q)ÎÂ[x], g1(x) ÎÂ[x] и deg g(x)³1, то есть многочлен f(x) приводим над полем действительных чисел.
)g1(x)=(x2+px+q)g1(x), причем (x2+px+q)ÎÂ[x], g1(x) ÎÂ[x] и deg g(x)³1, то есть многочлен f(x) приводим над полем действительных чисел.
§3. Многочлены с целыми коэффициентами
Пусть многочлен f(x)=bnxn+bn-1xn-1+…+b1x+b0 задан над полем Q, то есть все коэффициенты = рациональные числа. Приведем все коэффициенты к общему знаменателю (это возможно, так как всякое рациональное число может быть представлено в виде обыкновенной дроби) и вынесем за скобки общий числовой множитель, при необходимости сократив полученную дробь, тогда
f(x)= 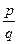 (anxn+an-1xn-1+…+a1x+a0), где aiÎZ,
(anxn+an-1xn-1+…+a1x+a0), где aiÎZ, 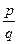 - несократимая дробь. Таким образом, f(x)=
- несократимая дробь. Таким образом, f(x)= 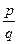 g(x) и g(x)ÎZ[x].
g(x) и g(x)ÎZ[x].
Многочлен с целыми коэффициентами будем называть примитивным многочленом, если все его коэффициенты взаимно просты. Справедлива следующая лемма:
Лемма 1. Всякий многочлен f(x)ÎQ[x] можно единственным образом с точностью до знака представить в виде произведения несократимой дроби на примитивный многочлен.
Доказательство. Выполним следующие операции:
1) приведем все коэффициенты к общему знаменателю s;
2) найдем наибольший общий делитель всех числителей d;
3) вынесем за скобку дробь 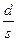 , при необходимости сократив ее.
, при необходимости сократив ее.
Получим требуемое представление f(x)= 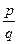 j(x), где
j(x), где 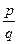 - несократимая дробь, а j(x) – примитивный многочлен.
- несократимая дробь, а j(x) – примитивный многочлен.
Предположим, что такое представление не единственное, то есть f(x)= 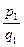 j1(x) и f(x)=
j1(x) и f(x)= 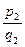 j2(x), где
j2(x), где 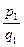 и
и 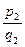 - несократимые дроби, а j1(x) и j2(x) – примитивные многочлены. Тогда
- несократимые дроби, а j1(x) и j2(x) – примитивные многочлены. Тогда 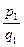 j1(x)=
j1(x)= 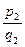 j2(x), это равносильно p1q2j1(x)=p2q1j2(x)=y(x).
j2(x), это равносильно p1q2j1(x)=p2q1j2(x)=y(x).
Так как j1(x) и j2(x) – примитивные многочлены, то p1q2 и p2q1 с точностью до знака являются наибольшими общими делителями коэффициентов многочлена y(x). Следовательно, ½p1q2½=½p1q2½Û 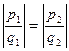 . Очевидно, что с точностью до знака многочлены j1(x) и j2(x) совпадают. Единственность доказана.
. Очевидно, что с точностью до знака многочлены j1(x) и j2(x) совпадают. Единственность доказана.
Лемма 2 (лемма Гаусса). Произведение примитивных многочленов есть примитивный многочлен.
Доказательство
Пусть j1(x)=anxn+an-1xn-1+…+a1x+a0 и j2(x)=bnxn+bn-1xn-1+…+b1x+b0 - примитивные многочлены, то есть an,…,a0,bn,…,b0ÎZ, (an,…,a1,a0)=1 и (bn,…,b1,b0)=1
Покажем, что j(x)=j1(x)j2(x)=c2nx2n+c2n-1x2n-1+...+c1x+c0 также примитивный многочлен. Так как j1 - примитивный многочлен, то для любого простого числа р найдется коэффициент, которой не делится на р. Аналогично для j2.
Предположим противное, что коэффициенты многочлена j(x) не взаимно просты. Пусть некоторое простое число р½ci "i=0¸2n. Так как р не может делить все коэффициенты многочленов j1(x) и j2(x), то можем предположить, что р делит все коэффициенты j1(x) от a0 до ak и не делит ak+1, р делит все коэффициенты j2(x) от b0 до bm и не делит bm+1 . Рассмотрим коэффициент сk+m=akbm+ak+1bm-1+…+ak+mb0+bm+1ak-1+…+bm+ka0.
Очевидно, что все слагаемые кроме первого делятся на р, а первое на р не делится, тогда сумма также не делится на р, то есть р не делит сk+m, что противоречит предположению, следовательно, j(x) - примитивный многочлен.
Теорема. Если многочлен с целыми коэффициентами приводим над полем Q, то он приводим и над кольцом Z.
Доказательство
Пусть f(x)ÎZ[x] приводим над полем Q, то есть f(x)=f1(x)f2(x), f1(x),f2(x)ÎQ[x]. По лемме 1 имеем f1(x)= 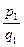 j1(x), f2(x)=
j1(x), f2(x)= 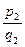 j2(x), где
j2(x), где 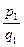 и
и 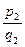 - несократимые дроби, а j1(x) и j2(x) – примитивные многочлены, тогда f(x)=
- несократимые дроби, а j1(x) и j2(x) – примитивные многочлены, тогда f(x)= 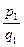
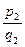 j1(x)j2(x)=
j1(x)j2(x)= 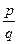 j1(x)j2(x), где
j1(x)j2(x), где 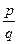 - несократимая дробь, а j1(x)j2(x) по лемме Гаусса примитивный многочлен. Так как j1(x),j2(x)ÎZ[x] и f(x)ÎZ[x], следовательно, ½q½=1 и f(x)=рj1(x)j2(x), то есть приводим над кольцом целых чисел.
- несократимая дробь, а j1(x)j2(x) по лемме Гаусса примитивный многочлен. Так как j1(x),j2(x)ÎZ[x] и f(x)ÎZ[x], следовательно, ½q½=1 и f(x)=рj1(x)j2(x), то есть приводим над кольцом целых чисел.
Из этой теоремы следует, что приводимость многочлена над полем рациональных чисел равносильна приводимости многочлена над кольцом целых чисел и наоборот. Аналогично обстоит дело и с корнями многочленов: если некоторое число a является корнем многочлена f(x), заданного над полем Q, то оно будет и корнем многочлена g(x) с целыми коэффициентами и наоборот.
В элементарной алгебре рассматриваются простейшие способы разложения многочлена с рациональными коэффициентами на множители. Для многочленов второй и третьей степени такое разложение осуществляется довольно просто благодаря следующей теореме.
теорема. Многочлен f(x) второй и третьей степени с рациональными коэффициентами тогда и только тогда приводим над полем рациональных чисел, когда он имеет, по меньшей мере, один рациональный корень.
Доказательство. Пусть f(х) - многочлен второй или третьей степени над полем рациональных чисел. Если f(х) имеет рациональный корень а, то f(х) делится на (х-а), т. е. f(х)=(х-а)f1(x), где f1(x) - многочлен над тем же самым полем рациональных чисел. При этом степень f1(x) будет равна 1 или 2. Таким образом, многочлен f(х) оказался приводимым над полем рациональных чисел.
Обратно, если многочлен f(х) приводим над полем рациональных чисел, то по меньшей мере один из множителей f(x) должен быть линейным; в противном случае произведение множителей имело бы степень, превосходящую 3, что невозможно. Следовательно, f(x)=(х-а)f1(x), где (х-а) и f1(x) - многочлены с рациональными коэффициентами, следовательно, а - рациональный корень f(x).
Пример. Разложить на неприводимые множители многочлен f(х)=х3+3х2+4х+2. Очевидно, что х=-1 – корень данного многочлена. действительно, f(-1)=-1+3-4+2=0. Разделим f(х) на (х+1) по схеме Горнера.
| х=-1 |
Получили f(х)=(х+1)(х2+2х+2). Многочлен х2+2х+2 не имеет рациональных корней и поэтому неприводим над полем рациональных чисел, следовательно, f(х)=(х+1)(х2+2х+2) и есть искомое разложение многочлена f(х).
Для многочленов выше третьей степени дело обстоит уже сложнее. Так, например, многочлен четвертой степени может оказаться приводимым над полем рациональных чисел и тогда, когда он не имеет рациональных корней, а именно он может разложиться в произведение двух неприводимых квадратных множителей. Тем не менее и для многочленов выше третьей степени с рациональными коэффициентами существуют методы разложения на множители. Мы, однако, не будем рассматривать эти практически громоздкие методы и ограничимся решением следующего вопроса: существует ли критерий, позволяющий определить, будет данный многочлен приводим над полем рациональных чисел или нет. Оказывается, такого критерия нет, более того, справедлив критерий, предложенный в 1850 г. Эйзенштейном и носящий его имя.
Критерий Эйзенштейна. Если f(x)=anxn+an-1xn-1+…+a1x+a0 - многочлен с целыми коэффициентами, причем an-1,…,a1,a0 делятся на некоторое простое число р, старший коэффициент аn не делится на р и свободный член а0, делясь на р, не делится на р2, то многочлен f(x) неприводим над кольцом целых чисел (полем рациональных чисел).
Доказательство
Предположим противное: пусть условие теоремы выполнено, но многочлен f(x)=anxn+an-1xn-1+…+a1x+a0 приводим над кольцом целых чисел, то есть f(x)=f1(x)f2(x), где f1(x),f2(x)ÎZ[x]. Пусть
f1(x)=bsxs+bs-1xs-1+…+b1x+b0,
f2(x)=cmxm+cm-1xm-1+…+c1x+c0,
тогда, приравнивая коэффициенты, получим:
a0=b0c0
a1=a0b1+b1a0
………………
ak= 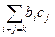
………….
an=bscm.

 Так как р½a0, то есть р½b0c0, то в силу того, что р – простое, р½b0Ú р½c0. Так как р2½a0, тогда р не может делить оба сомножителя. Не ограничивая общности доказательства, будем считать, что р½c0 и р½b0, тогда (р, c0)=1. Не все коэффициенты многочлена f1(x) делятся на р, так как в этом случае на р делилось бы и an=bscm. Пусть bk – первый коэффициент, который не делится на р, то есть р½b0, р½b1,…, р½bk-1 и р не делит bk. Рассмотрим ak=
Так как р½a0, то есть р½b0c0, то в силу того, что р – простое, р½b0Ú р½c0. Так как р2½a0, тогда р не может делить оба сомножителя. Не ограничивая общности доказательства, будем считать, что р½c0 и р½b0, тогда (р, c0)=1. Не все коэффициенты многочлена f1(x) делятся на р, так как в этом случае на р делилось бы и an=bscm. Пусть bk – первый коэффициент, который не делится на р, то есть р½b0, р½b1,…, р½bk-1 и р не делит bk. Рассмотрим ak= 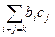 =bkc0+bk-1c1+…+b2ck-2+b1ck-1+b0ck. Получили, что ak, bk-1,…,b2,b1,b0 делятся на р , следовательно, на р делится и bkc0, но (р, c0)=1, тогда р½bk. получили противоречие. Критерий доказан.
=bkc0+bk-1c1+…+b2ck-2+b1ck-1+b0ck. Получили, что ak, bk-1,…,b2,b1,b0 делятся на р , следовательно, на р делится и bkc0, но (р, c0)=1, тогда р½bk. получили противоречие. Критерий доказан.
Из этого критерия сразу получается решение нашего вопроса, а именно: нетрудно теперь убедиться, что неприводимыми над полем рациональных чисел (над кольцом целых чисел) могут быть многочлены любой заданной степени п > 1. Таким образом, поле рациональных чисел налагает на неприводимость многочленов меньше ограничений, чем поле действительных чисел и поле комплексных чисел.
Все доказанное нами по поводу приводимости многочленов над числовыми полями можно обобщить следующим образом.
| C[x] | Â[x] | Q[x], Z[x] |
| Многочлен первой степени неприводим | ||
| Всякий многочлен, степени n³2 приводим | Всякий многочлен, степени n³3 приводим | Существуют неприводимые многочлены любой степени |
Дата добавления: 2020-10-25; просмотров: 851;











