Связка прямых и плоскостей

1.Связкой плоскостей называется множество всех плоскостей, проходящих через одну и ту же точку ; точка называется центром этой связки. Связку плоскостей с центром будем обозначать .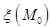

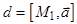Связка плоскостей вполне определяется заданием ее центра . Через любую прямую , не проходящую через центр связки проходит единственная плоскость связки .

Пусть точка произвольная точка пространства, отличная от центра связки 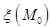, 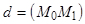. Всякая плоскость пучка проходит через точку и, значит, принадлежит связке 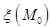. Поэтому через любую точку 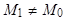проходит пучок плоскостей связки 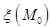. Отсюда следует, что через любую прямую 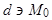проходит пучок плоскостей связки .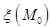

Зададим аффинную систему координат 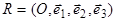в пространстве, и пусть центр связки 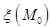плоскостей имеет координаты 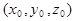. Плоскость , определяемая уравнением 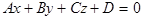, проходит через точку и, значит, принадлежит связке плоскостей 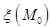тогда и только тогда, когда

.

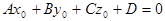Поэтому всякая плоскость определяется уравнением вида:

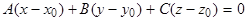(1)

и, обратно, уравнение (1), в котором не равны нулю одновременно, определяет плоскость связки .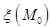

Центр связки плоскостей 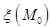может быть задан как точка пересечения трех ее плоскостей , ,

: ,

: ,

:

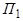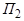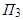
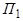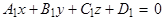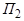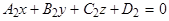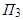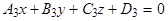
при условии, что

Это условие означает, что плоскости 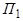, , 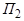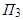имеют единственную общую точку . Отсюда следует, что векторы 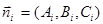, 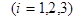линейной независимы, и поэтому вектор соответствующий плоскости можно разложить по векторам базиса :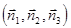

где не равны нулю одновременно. Переходя к координатам, получим :

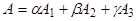
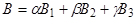(2)

Так как , то 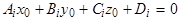( 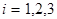) (3). Заменив в уравнении (1) коэффициенты 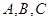по формулам (2) и использовав равенства (3), приведем уравнение (1) к виду:

( )+ ( )+

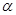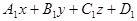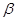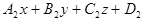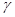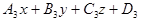+ ( )=0 (4)

Таким образом, произвольная плоскость связки 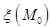определяется уравнением (4) , и всякое уравнение вида (4) при , не равных нулю одновременно, определяет плоскость связки 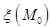. Следовательно, уравнение (4) есть уравнение связки плоскостей 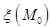. Плоскость однозначно определяется заданием отношений в уравнении (4).

2.Множество плоскостей, параллельных данной прямой 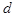, называется связкойплоскостей, параллельныхпрямой 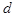. Связка плоскостей параллельных прямой 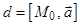, вполне определяется заданием направляющего вектора 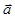этой прямой. Поэтому эту связку плоскостей будем обозначать через .

Плоскость , определяемая уравнением Ax+By+Cz+D=0 принадлежит связке , тогда и только тогда когда 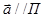, то есть когда .

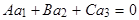3.Связкойпрямых называется множество всех прямых пространства, проходящих через одну и ту же точку ; точка называется центром этой связки. Связку прямых с центром будем обозначать .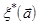

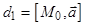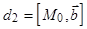
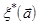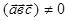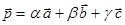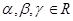Пусть , три прямые связки , не лежащие в одной плоскости: . Прямая , где , не равны нулю одновременно, есть произвольная прямая связки 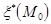, и всякая прямая связки 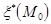имеет направляющий вектор 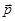, который может быть разложен по трем некомпланарным векторам - направляющим векторам прямых 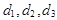из .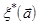

В качестве векторов можно взять координатные векторы 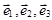аффинной системы координат .

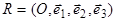Прямая 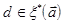однозначно определяется заданием отношений 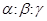координат направляющего вектора 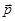прямой 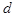относительно базиса ( ), составленного из направляющих векторов трех прямых 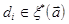, 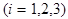не лежащих в одной плоскости.

Через любую точку проходит единственная прямая 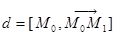связки 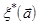. Три прямые связки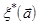 , , 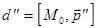принадлежат одному пучку 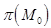прямых тогда и только тогда, когда векторы ,

,

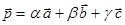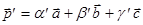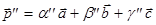
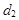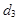
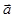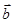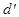
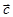
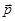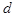
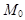
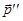
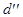
компланарны, то есть

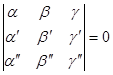
4.Отношение // параллельности на множестве 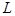всех прямых пространства является отношением эквивалентности.

Элементы фактор-множества 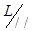называется связкамипараллельныхпрямых или направлениями в широком смысле слова в пространстве. Значит, связка параллельных прямых - это множество всех прямых пространства, параллельных данной прямой ( представителю данной связки).

Связка параллельных прямых вполне определяется заданием какого-либо вектора 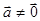,параллельного прямым связки. Поэтому такую связку прямых будем обозначать через .

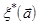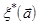Прямая принадлежит связке тогда и только тогда, когда вектор 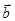коллинеарен вектору :

.

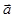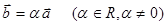Через любую точку пространства 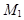пространства проходит единственная прямая 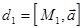связки .

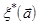Три прямые связки 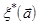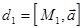, , 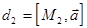принадлежат одному пучку 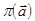прямых тогда и только тогда, когда прямые 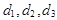в одной плоскости, и, значит, векторы , , 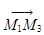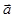компланарны, то есть для таких векторов выполняется условие

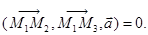
5.Множество 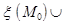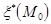называется связкойпрямых и плоскостей с центром 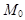. Каждые две (различные) плоскости связки пересекаются по прямой 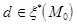и каждая прямая 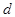связки 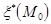является осью пучка плоскостей связки . Следовательно, множество прямых по которым пересекаются плоскости связки , есть связка прямых .

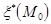И обратно, каждые две (различные) прямые связки 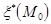определяют плоскость 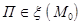через них проходящую , и каждой плоскости 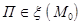принадлежит пучок прямых связки .

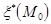Таким образом, связка плоскостей порождает связку 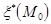прямых и обратно.

Множество 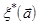называется связкойпрямых и плоскостей, параллельныхпрямой 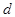с направляющим вектором 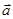. Связка 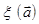плоскостей порождает связку 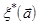прямых и обратно.

Литература

1. Атанасян Л.С., Геометрия ч.I, М., Просвещение,1973.

2. Атанасян Л.С., Базылев В.Т. Геометрия ч.I, М., Просвещение,1986.

3. Базылев В.Т.,Дуничев К.И., Иваницкая В.П. Геометрия ч.I, М., Просвещение,1974.

4. Егоров И.П., Геометрия, М., Просвещение,1979.

5. Погорелов А.В. Геометрия , М., Просвещение,1983.