Математическое моделирование электромеханических переходных процессов в электроприводах
Общие понятия:
Переходным процессом (ПП) в электроприводах называют режимы, которые возникают при переходе от одного установившегося состояния к другому. Основным признаком возникновения ПП является изменение угловой скорости вращения. Одновременно изменяются моменты и силы, действующие на элементы электропривода, а также тепловое состояние этих элементов. В зависимости от характера возмущающих воздействий различают:
а) естественные ПП – пуск, торможение, регулирование скорости вращения, изменение нагрузки на валу;
б) искусственные ПП, которые возникают в результате неисправностей в двигателе, системе передачи, в системе управления или в производственном механизме. При анализе ПП удобно разделять переходные режимы на 2 вида:
1) электромеханические ПП;
2) тепловые ПП.
50.1 Электромеханические переходные процессы
Любой электромеханический ПП в ЭП-х, который характеризуется одновременным изменением угловой скорости, а также моментов воздействующих на элементы ЭП описываются:
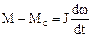 . (1)
. (1)
В зависимости от постановки задачи анализ ПП может заключаться либо в определении временных характеристик ПП-а (длительность пуска, длительность торможения, время изменения скорости от ω1 до ω2) при известных величинах и характера изменения моментов. Либо определения моментов ЭП при известных временных показателях. При анализе используют не классическое уравнение движения, а уравнение движения в инженерных координатах. Замена 

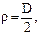 тогда
тогда 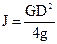 , откуда следует
, откуда следует 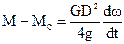 . (2)
. (2)
Уравнение (2) – уравнение движения в инженерных координатах.
G – сила тяжести,
D – приведенный диаметр,
g – ускорение свободного падения,
GD2 – маховый момент.
ЭП как система содержит в своей структуре передаточное звено (звенья) и имеется как минимум 2 вала, вращающиеся с различными скоростями. Поэтому для анализа электромеханического ПП необходимо привести все статические моменты сопротивления и моменты инерции к одному валу (к скорости одного вала (двигателя)). Приведение статических моментов сопротивления и моментов инерции отдельных элементов ЭП К валу двигателя:
МС.М - ? J - ?

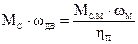 , откуда МС:
, откуда МС: 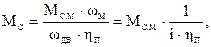
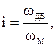
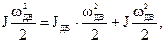
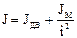 .
.
50.2 Анализ электромеханических переходных процессов
Определение длительности ПП при известных величинах и характере изменения моментов. При любом характере изменения моментов решение задачи в общем виде имеет вид:
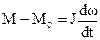 , откуда
, откуда 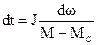 и соответственно
и соответственно 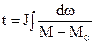 .
.
В зависимости от того какой характер имеют зависимости изменения М и МС от ω сложность решения задачи м/б различной.
Так, если вращающий момент двигателя изменяется нелинейно, МС – const. Пример: АД – поршневой насос. При решении такой задачи вводится эффективный момент двигателя, МЭФ, который определяется по паспортным данным асинхронных двигателей с помощью эмпирических формул различной степенью точности. Время пуска определяется как:
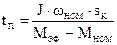 ,
, 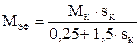 .
.
В случаях, когда и вращающий ЭММ изменяется нелинейно и статический момент, МС изменяются также нелинейно, использование точных аналитических методов становится невозможным, поэтому при решении таких задач применяют либо приближенные графические методы расчета, либо более точные и универсальные – графоаналитические методы, либо более удобные, но менее универсальные - алгоритмические.
В качестве графического метода расчета является метод пропорций. В качестве графоаналитического – метод площадей. В качестве алгоритмического – метод Симпсона.
Все перечисленные методы расчета основаны на том предположении, в соответствии с которым бесконечно малые приращения ω и t, т. е. dω и dt заменяются малыми конечными: 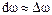 ,
, 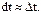
Уравнение движения двигателя электропривода: 
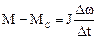 .
.
Для метода пропорций существенным является уравнение:
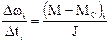 .
.
Графический метод решения уравнения движения обладает преимуществом, которое связано с физичностью процесса, но не обладает точностью, а также громоздок.
Наиболее универсальным и достаточно точным (по сравнению с алгоритмическими методами), обеспечивающим более точное совпадение с экспериментальными данными является графоаналитический метод площадей.
Последовательность расчета времени запуска двигателя рассмотрим с помощью следующего примера: АД с кз ротором приводит во вращение центробежный насос.
Последовательность расчета:
Уравнение механической характеристики АД 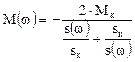 .
.
Уравнение механической характеристики насоса
 |
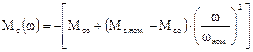 ,
,
Уравнение совместной механической характеристики : Мд(w) = М(w) - Мс(w).

Разбиваем ось координат на ряд участков DwI, при этом, Dw1 =Dw2 = … =Dwi при этом точность расчета будет зависеть от количества участков разбиения.
Совместная механическая характеристика механизма заменяется аппроксимирующей ломаной кривой и считается, что на каждом участке разбиения
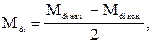 Общая длительность пуска
Общая длительность пуска 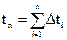 ,где
,где 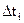 – определяется для каждого участка разбиения по формуле
– определяется для каждого участка разбиения по формуле 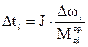 .
.
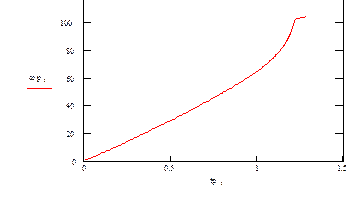
Суммарное время разгона электропривода до номинальной скорости
Расчет времени торможения производим по методу площадей, аналогично предыдущему пункту.
50.3 Тепловые переходные процессы в электроприводах
Процесс работы ЭД сопровождается потерями мощности (активной), которая складывается из потерь в обмотках (эл. потерь), сердечника (магнитных потерь) и механической системы (мех. потерь). Эти потери выражаются в виде нагрева отдельных агрегатов двигателя, количество тепла, выделяющееся в двигателе dQ:
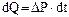 ,
,
dt – длительность работы двигателя, ΔP – потери мощности.
В начальный период работы двигателя после его включения большая часть выделившегося тепла будет приходиться на нагрев самого двигателя, часть рассеивается в окружающую среду (ОС). По мере нагрева ЭД доля в ОС будет увеличиваться, доля тепла, идущего на нагрев двигателя будет уменьшаться. При некоторой температуре Д, равной установившейся (  ) дальнейший нагрев Д прекращается и все тепло выделившееся в Д рассеивается в ОС, устанавливается т. н. установившийся тепловой режим. Значение температуры, равной установившейся будет зависеть от нагрузки Д.
) дальнейший нагрев Д прекращается и все тепло выделившееся в Д рассеивается в ОС, устанавливается т. н. установившийся тепловой режим. Значение температуры, равной установившейся будет зависеть от нагрузки Д.
Реальные тепловые процессы, происходящие в ЭП являются весьма сложными, поэтому для удобства анализа этих процессов примем следующие допущения:
1) двигатель представляет из себя абсолютно однородное тело, теплоемкость по всему объему тела Д одинакова;
2) теплоотдача со всех точек поверхности Д также одинакова.
Для анализа тепловых процессов используются следующие величины:
dQ – общее количество тепла, выделившееся в двигателе; ккал
dQПОГЛ – количество или часть этого тепла, идущее на нагрев самого двигателя;
dQОТД – часть этого тепла рассеивающееся в ОС; ккал
ΔР – потери мощности, кВт;
С – теплоемкость, ккал;
А – теплоотдача, ккал/(гр.·с);
τ – превышение температуры двигателя (температура перегрева двигателя),
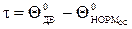 .
.
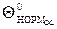 - нормирующая температура,
- нормирующая температура, 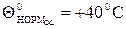 .
.
Дата добавления: 2016-07-22; просмотров: 3133;











