Искусственный нейрон и функции активации
Биологический нейрон содержит сому (тело нейрона), совокупность отростков – дендритов, по которым в нейрон поступают входные сигналы и отросток – аксон, передающий выходной сигнал нейрона другим нейронам. Точка соединения дендрита и аксона называется синапсом. Общее число нейронов в головном мозгу человека превышает 100 миллиардов, при этом один нейрон соединен более чем с 10 тысячами соседних нейронов. Время срабатывания нейрона составляет около одной миллисекунды, чуть меньше тратится на передачу сигнала между двумя нейронами. Таким образом, биологический нейрон – чрезвычайно медленный процессорный элемент, уступающий быстродействию современных компьютеров в миллионы раз. Тем не менее, в целом мозг способен за доли секунды решать задачи, которые не может решить и суперкомпьютер (например, узнать лицо человека, показанное в непривычном ракурсе).
Искусственным нейроном называется простой элемент в виде следующей структуры (рис.6.1) [1].

Рис. 6.1. Искусственный нейрон: 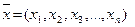 - вектор входных переменных (дендритов);
- вектор входных переменных (дендритов); 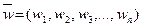 - вектор синаптических весов;
- вектор синаптических весов;
S – сома; y – выход (аксон)
Сначала вычисляется взвешенная сумма V входных переменных (скалярное произведение):
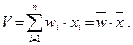
Затем полученная сумма (потенциал нейрона) сравнивается с заданной пороговой величиной W0. Если V 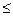 W0, то нейрон «не срабатывает», в противном случае вычисляется функция активации (решающая функция) f . При этом
W0, то нейрон «не срабатывает», в противном случае вычисляется функция активации (решающая функция) f . При этом
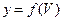 .
.
Величину порогового барьера можно рассматривать как еще один весовой коэффициент при постоянном входном сигнале.
Функции активации могут быть различных видов: линейная, ступенчатая, линейная с насыщением, многопороговая. Наиболее распространенной является сигмоидная функция с выходными значениями в интервале (0,1):
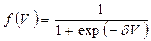
или в интервале (-1,1):
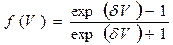 .
.
Коэффициент 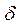 определяет крутизну сигмоида. Поскольку сигмоидная функция является гладким отображением
определяет крутизну сигмоида. Поскольку сигмоидная функция является гладким отображением 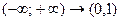 , крутизну
, крутизну 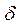 можно учесть через величины весов и порогов, и без ограничения общности можно полагать
можно учесть через величины весов и порогов, и без ограничения общности можно полагать 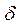 = 1. Чтобы учесть особенности конкретной задачи, могут быть выбраны различные другие функции активации – гауссова, синусоидальная, всплески и т.д.
= 1. Чтобы учесть особенности конкретной задачи, могут быть выбраны различные другие функции активации – гауссова, синусоидальная, всплески и т.д.
Дата добавления: 2016-07-22; просмотров: 2603;











