С ожиданием и ограниченной длинной очереди
Имеется n-канальная СМО с ожиданием, в которой количество заявок, стоящих в очереди, ограничено числом m, т.е. заявка, заставшая все каналы занятыми, становится в очередь, только если в ней находится менее m заявок.
Если число заявок в очереди равно m, то последняя прибывшая заявка в очередь не становится и покидает систему необслуженной.
Системы с ограниченной очередью являются обобщением двух рассмотренных ранее СМО: при m = 0 получаем СМО с отказами, при m = ¥ получаем СМО с ожиданием.
· Вероятность простоя (того, что все обслуживающие аппараты свободны, нет заявок):
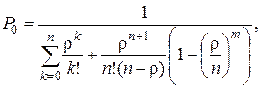 (4.18)
(4.18)
· Вероятность отказа в обслуживанииравна вероятности 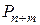 того, что в очереди уже стоят m заявок:
того, что в очереди уже стоят m заявок:
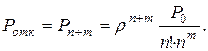 (4.19)
(4.19)
· Относительная пропускная способность есть величина, дополняющая вероятность отказа до 1, т.е. вероятность обслуживания:
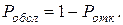
(4.20)
· Абсолютная пропускная способностьопределяется равенством:
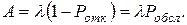 (4.21)
(4.21)
· Среднее число занятых обслуживанием каналов:
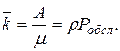 (4.22)
(4.22)
· Среднее число заявок в очереди (средняя длина очереди)
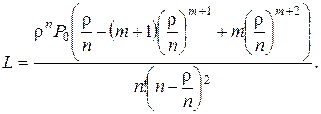 (4.23)
(4.23)
· Среднее время ожидания обслуживания в очереди
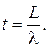 (4.24)
(4.24)
· Среднее число заявок в системе
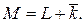 (4.25)
(4.25)
· Среднее время пребывания заявки в системе
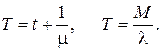 (4.26)
(4.26)
Дата добавления: 2020-10-14; просмотров: 512;











