Структура и классификация систем массового обслуживания
Нередко возникает необходимость в решении вероятностных задач, связанных с системами массового обслуживания (СМО), примерами которых могут быть:
• Билетные кассы;
• Ремонтные мастерские;
• Торговые, транспортные, энергетические системы;
• Системы связи;
• и т.д.
Общность таких систем выявляется в единстве математических методов и моделей, применяемых при исследовании их деятельности.
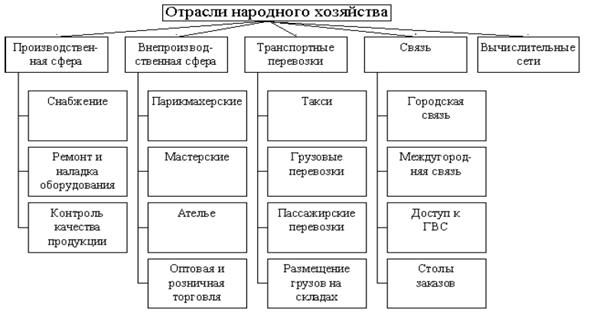
Рис. 4.1. Основные сферы применения ТМО
На вход в СМО поступает поток требований на обслуживание. Например, клиенты или пациенты, поломки в оборудовании, телефонные вызовы. Требования поступают нерегулярно, в случайные моменты времени. Случайный характер носит и продолжительность обслуживания. Это создает нерегулярность в работе СМО, служит причиной ее перегрузок и недогрузок.
Системы массового обслуживания обладают различной структурой, но обычно в них можно выделить четыре основных элемента:
1. Входящий поток требований.
2. Накопитель (очередь).
3. Приборы (каналы обслуживания).
4. Выходящий поток.
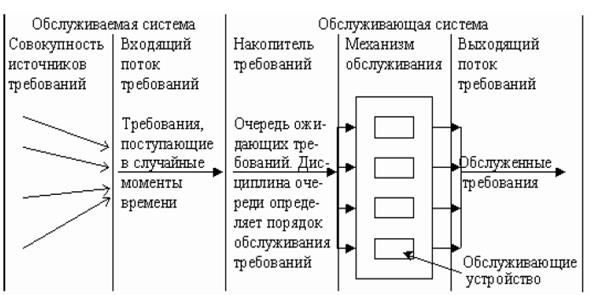
Рис. 4.2. Общая схема систем массового обслуживания
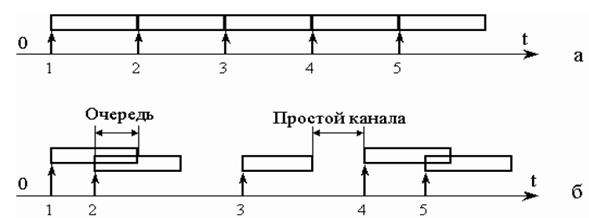
Рис. 4.3. Модель работы системы
(стрелками показаны моменты поступления требований в
систему, прямоугольниками – время обслуживания)
На рис.4.3 а представлена модель работы системы с регулярным потоком требований. Поскольку известен промежуток между поступлениями требований, то время обслуживания выбрано так, чтобы полностью загрузить систему. Для системы со стохастическим потоком требований ситуация совершенно иная – требования приходят в различные моменты времени и время обслуживания тоже является случайной величиной, которое может быть описано неким законом распределения (рис.4.3 б).
В зависимости от правил образования очереди различают следующие СМО:
1) системы с отказами, в которых при занятости всех каналов обслуживания заявка покидает систему необслуженной;
2) системы с неограниченной очередью, в которых заявка встает в очередь, если в момент ее поступления все каналы обслуживания были заняты;
3) системы с ожиданием и ограниченной очередью, в которых время ожидания ограниченно какими-либо условиями или существуют ограничения на число заявок, стоящих в очереди.
Рассмотрим характеристики входящего потока требований.
Поток требований называется стационарным, если вероятность попадания того или иного числа событий на участок времени определенной длины зависит только от длины этого участка.
Поток событий называется потоком без последствий, если число событий, попадающих на некоторый участок времени, не зависит от числа событий, попадающих на другие.
Поток событий называется ординарным, если невозможно одновременное поступление двух или более событий.
Поток требований называется пуассоновским(или простейшим), если он обладает тремя свойствами: стационарен, ординарен и не имеет последствий. Название связано с тем, что при выполнении указанных условий число событий, попадающих на любой фиксированный интервал времени, будет распределен по закону Пуассона.
Интенсивностью потока заявок λ называется среднее число заявок, поступающих из потока за единицу времени.
Для стационарного потока интенсивность постоянна. Если τ – среднее значение интервала времени между двумя соседними заявками, то 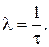 В случае пуассоновского потока вероятность поступления на обслуживание m заявок за промежуток времени t определяется по закону Пуассона:
В случае пуассоновского потока вероятность поступления на обслуживание m заявок за промежуток времени t определяется по закону Пуассона:
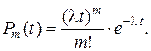
Время между соседними заявками распределено по экспоненциальному закону с плотностью вероятности 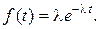
Время обслуживания 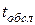 является случайной величиной и подчиняется показательному закону распределения с плотностью вероятности
является случайной величиной и подчиняется показательному закону распределения с плотностью вероятности 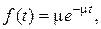 где μ – интенсивность потока обслуживания, т.е. среднее число заявок, обслуживаемых в единицу времени,
где μ – интенсивность потока обслуживания, т.е. среднее число заявок, обслуживаемых в единицу времени, 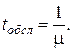
Отношение интенсивности входящего потока к интенсивности потока обслуживания называется загрузкой системы 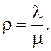
Загрузка – это среднее число заявок, приходящих за среднее время обслуживания одной заявки.
Марковский процесс
Система массового обслуживания представляет собой систему дискретного типа с конечным или счетным множеством состояний, а переход системы из одного состояния в другое происходит скачком, когда осуществляется какое-нибудь событие.
Процесс называется процессом с дискретными состояниями, если его возможные состояния 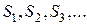 можно заранее перенумеровать, и переход системы из состояния в состояние происходит практически мгновенно.
можно заранее перенумеровать, и переход системы из состояния в состояние происходит практически мгновенно.
Такие процессы бывают двух типов: с дискретным или непрерывным временем.
В случае дискретного времени переходы из состояния в состояние могут происходить в строго определенные моменты времени. Процессы с непрерывным временем отличаются тем, что переход системы в новое состояние возможен в любой момент времени.
Случайным процессом называется соответствие, при котором каждому значению аргумента (в данном случае – моменту из промежутка времени проводимого опыта) ставится в соответствие случайная величина (в данном случае – состояние СМО). Случайной величиной называется величина, которая в результате опыта может принять одно, но неизвестное заранее, какое именно, числовое значение из данного числового множества.
Поэтому для решения задач теории массового обслуживания необходимо этот случайный процесс изучить, т.е. построить и проанализировать его математическую модель.
Случайный процесс называется марковским, если для любого момента времени 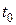 вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент
вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент 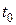 и не зависят от того, когда и как система пришла в это состояние.
и не зависят от того, когда и как система пришла в это состояние.
Переходы системы из состояния в состояние происходит под действием каких-то потоков (поток заявок, поток отказов). Если все потоки событий, приводящие систему в новое состояние, – простейшие пуассоновские, то процесс, протекающий в системе, будет марковским, так как простейший поток не обладает последствием: в нем будущее не зависит от прошлого.
Пример марковского процесса: система 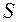 – счетчик в такси. Состояние системы в момент
– счетчик в такси. Состояние системы в момент 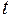 характеризуется числом километров (десятых долей километров), пройденных автомобилем до данного момента. Пусть в момент
характеризуется числом километров (десятых долей километров), пройденных автомобилем до данного момента. Пусть в момент 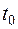 счетчик показывает
счетчик показывает 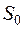 . Вероятность того, что в момент
. Вероятность того, что в момент 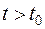 счетчик покажет то или иное число километров (точнее, соответствующее число рублей)
счетчик покажет то или иное число километров (точнее, соответствующее число рублей) 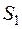 , зависит от
, зависит от 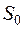 , но не зависит от того, в какие моменты времени изменялись показания счетчика до момента
, но не зависит от того, в какие моменты времени изменялись показания счетчика до момента 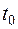 .
.
Многие процессы можно приближенно считать марковскими. Например, процесс игры в шахматы: система 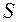 – группа шахматных фигур. Состояние системы характеризуется числом фигур противника, сохранившихся на доске в момент
– группа шахматных фигур. Состояние системы характеризуется числом фигур противника, сохранившихся на доске в момент 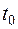 . Вероятность того, что в момент
. Вероятность того, что в момент 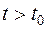 материальный перевес будет на стороне одного из противников, зависит в первую очередь от того, в каком состоянии находится система в данный момент
материальный перевес будет на стороне одного из противников, зависит в первую очередь от того, в каком состоянии находится система в данный момент 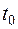 , а не от того, когда и в какой последовательности исчезли фигуры с доски до момента
, а не от того, когда и в какой последовательности исчезли фигуры с доски до момента 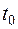 .
.
Дата добавления: 2020-10-14; просмотров: 673;











