К задаче линейного программирования
Игра m×n в общем случае не имеет наглядной геометрической интерпретации. Решение достаточно трудоемко при больших m и n, но может быть сведено к задаче линейного программирования.
Пример решения задачи. Предприятие может выпускать 3 вида продукции А1, А2 и А3, получая при этом прибыль, зависящую от спроса, который может быть в одном из 4-х состояний (В1, В2, В3, В4). Элементы платежной матрицы характеризуют прибыль, которую получат при выпуске i-й продукции при j-м состоянии спроса. Определить оптимальные пропорции в выпускаемой продукции, гарантирующие максимизацию средней величины прибыли при любом состоянии спроса, считая его определенным. Задача сводится к игровой модели, в которой игра предприятия А против спроса В задана платежной матрицей.
Таблица 2.5
Платежная матрица игры
| В1 | В2 | В3 | В4 | α | |
| А1 | |||||
| А2 | |||||
| А3 | |||||
| β |
Прежде чем решить задачу, попытаемся упростить игру, проведя анализ платежной матрицы и отбросив заведомо невыгодные и дублирующие стратегии.
Для игрока В невыгодна вторая стратегия (столбец В2), так как все элементы этого столбца больше или равны элементам столбца В1, то есть при любой стратегии, выбранной игроком А, игрок В проигрывает больше в случае выбора второй стратегии вместо первой.
Поскольку a ¹ b, следовательно седловая точка отсутствует, решение будем искать в смешанных стратегиях.
Чтобы привести игру к задаче линейного программирования, обозначим:
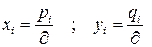 .
.
Получим две взаимно двойственные задачи линейного программирования:
Для первого игрока:
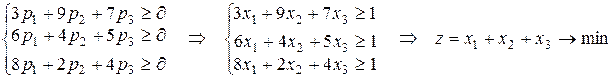 (так как
(так как 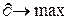 , то
, то 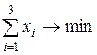 .
.
Поскольку 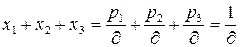 .
.
И для второго игрока:
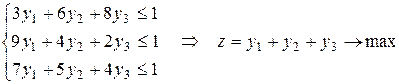
Вторую задачу на максимум решать легче. Решаем ее симплексным методом. Получаем следующий результат:
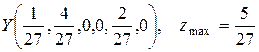 .
.
Последняя запись целевой функции имеет вид:
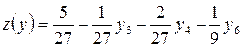 .
.
Следовательно, можем записать решение взаимно двойственной задачи, то есть задачи для первого игрока, используя теорию двойственности. Это решение будет иметь вид:
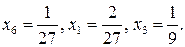
Цена игры 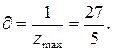
Найдем вероятности выбора стратегий:
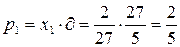 ,
, 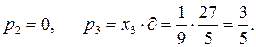
То есть 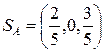 .
.
Данный результат означает, что предприятие должно выпустить 40 % продукции А1 и 60 % продукции А3, а продукцию А2 выпускать не надо. Тогда максимально гарантированное из минимально возможных значений средней величины прибыли составит 5,4 ден. ед., независимо от спроса покупателей.
Дата добавления: 2020-10-14; просмотров: 595;











