Что означают следующие термины и понятия?
| Игра | Комбинаторная игра |
| Игроки | Стратегическая игра |
| Стратегия | Непрерывная игра |
| Ход | Матричная игра |
| Личный ход | Платежная матрица |
| Случайный ход | Решение игры |
| Функция выигрыша | Оптимальные стратегии |
| Парная игра | Максиминная стратегия |
| Множественная игра | Минимаксная стратегия |
| Игра с нулевой суммой | Устойчивость решения |
| Игра с постоянной разностью | Цена игры |
| Конечная игра | Верхняя цена игры |
| Бесконечная игра | Нижняя цена игры |
| Кооперативная игра | Чистая стратегия |
| Коалиционная игра | Смешанная стратегия |
| Бескоалиционная игра | Седловая точка |
Теперь вы должны уметь:
o составлять экономико-математические модели задач, применяя методы теории игр;
o решать матричные игры графическим методом;
o приводить задачи теории игр к задачам линейного программирования;
o определять, разрешима ли игра в чистых стратегиях;
o определять оптимальные смешанные стратегии для игроков, то есть находить вероятности применения чистых стратегий;
o классифицировать игру;
o анализировать результаты решения игры;
o решать игру аналитическим способом, если в игре участвуют только два игрока и у одного из них имеется только две стратегии.
Контрольные вопросы:
1.Понятие игры.
2.Какие проблемы решает теория игр (теория конфликтных ситуаций)?
3.Классификация игр.
4.Что значит решить игру?
5.Что такое платежная матрица?
6.Что называется чистой ценой игры?
7.Когда в игре существует седловая точка?
8.Геометрическая интерпретация игры.
9.Схема решения игры.
10.Понятие смешанных стратегий, когда они необходимы, как применить их на практике.
11.Какие типы экономических задач сводятся к игровой модели?
СЕТЕВОЕ ПЛАНИРОВАНИЕ И УПРАВЛЕНИЕ
Теория графов тесно связана со многими направлениями математического моделирования. Особенно важная взаимосвязь существует между теорией графов и исследованием операций, теорией игр, сетевым планированием и управлением.
Граф – это конструкция из вершин и ребер. Вершины – это точки, а ребра – соединяющие их линии. Ребра могут быть ориентированными дугами. Граф называется Эйлеровым, если существует путь, позволяющий прийти в ту же вершину, из которой вышли, пройдя по каждому ребру, только один раз. Граф называется Гамильтоновым, если существует путь, позволяющий обойти все вершины, заходя в каждую только один раз. Деревом называется граф, любые две вершины которого соединены только одним ребром.
С помощью теории графов в детстве многие из вас решали задачу: нарисовать домик, не отрывая ручки от бумаги, то есть рисовали Эйлеровый граф. Гамильтонов граф применяется курьерами, которым необходимо обойти несколько организаций, естественно, заходя в каждую один раз, и они стремятся минимизировать свой общий путь – так называемая задача коммивояжера.
Пример решения задачи.
Сетевая задача, которая решается как транспортная.
Компания имеет восемь крупных оптовых складов. Отдел сбыта принял решение значительно снизить цену одного дорогостоящего изделия с целью ликвидации образовавшегося запаса этих изделий. Руководство намерено разместить имеющиеся в наличии запасы на указанных восьми складах в соответствии с прогнозами сбыта в этих районах. Таким образом, надо перераспределить некоторую часть запасов. Числа у складов – это избыток или недостаток товара. Склады 2, 4, 5, 6, 7 – промежуточные. Все другие склады – источники, если избыток товаров и стоки – если требуется дополнительный запас. Сij – затраты на перевозку одного изделия со склада i на склад j.
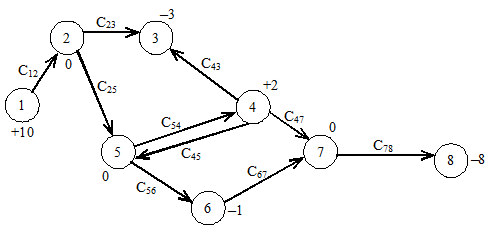
Рис. 3.1. Схема перевозок товаров между складами
Задание для самостоятельной работы. Составить экономико-математическую модель транспортной задачи.
Дата добавления: 2020-10-14; просмотров: 618;











