Однонаправленные функции

Реализация асимметричных криптосистем основана на использовании однонаправленных функций.

Пусть X и Y – некоторые произвольные множества. Функция 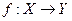называется однонаправленной функцией, если для любого элемента 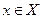можно легко вычислить его образ 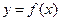, однако, зная элемент 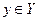, достаточно сложно получить его прообраз 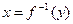, хотя такой элемент x однозначно существует хотя бы один.

Одним из основных критериев, по которому функцию f можно считать однонаправленной, является отсутствие эффективных алгоритмов обратного преобразования 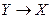, что не позволяет обратить данную функцию за приемлемое время.

Рассмотрим несколько примеров однонаправленных функций, имеющих большое значение для криптографии.

Целочисленное умножение

Вычисление произведения двух очень больших целых чисел P и Q (N=P*Q) является несложной задачей для ЭВМ. Однако, решение обратной задачи, заключающейся в нахождении делителей P и Q большого числа N (в особенности, когда P и Q – большие простые числа), является практически неразрешимой задачей при больших N. Если N»2⁶⁶⁴ и P»Q, то задача факторизации не разрешима за приемлемое время на современных ЭВМ. Поэтому целочисленное умножение является однонаправленной функцией.

Модульная экспонента

Возведение очень большого числа A в очень большую степень x по любому модулю M ( 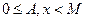), то есть вычисление 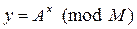является несложной задачей для ЭВМ. Однако решение обратной задачи – нахождения степени x по известным у,A,M такой, что 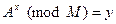(задача дискретного логарифмирования, 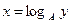), практически не разрешима за приемлемое время на современных ЭВМ (эффективного алгоритма вычисления дискретного логарифма пока не найдено). Поэтому модульная экспонента является однонаправленной функцией.

Кроме однонаправленных функций важное значение для криптографии с открытым ключом имеют однонаправленные функции с «потайным входом», эффективное обращение которых возможно, если известен секретный «потайной ход» (секретное число или другая информация, ассоциируемая с функцией).