Алгоритм шифрования RSA
Алгоритм RSA был предложен в 1978 году Р.Райвестом, А. Шамиром, А. Адлеманом и был назван по первым буквам фамилий его авторов. Данный алгоритм стал первым алгоритмом шифрования с открытым ключом. Надежность данного алгоритма основывается на трудности факторизации больших чисел и вычисления дискретных логарифмов [20,25].
В криптосистеме RSA открытый ключ ОК, секретный ключ СК, исходное сообщение М и шифротекст С являются целыми числами от 0 до N-1, где N – модуль.
Пусть пользователь А является получателем сообщения, которое ему должен переслать отправитель B.
Пользователь A должен вначале сгенерировать ключевую пару RSA, это он делает следующим образом.
Алгоритм формирования ключевой пары пользователем А
1. Выбираем случайные большие простые числа P и Q. Для обеспечения максимальной безопасности P и Q выбирают примерно равной длины и хранят в секрете.
2. Вычисляем модуль 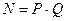 ,
, 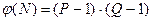 , где
, где 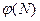 - функция Эйлера.
- функция Эйлера.
3. Открытый ключ ОКА выбирается случайно таким образом, чтобы выполнялись следующие условия:
1<ОКA< 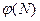 , НОД(ОКА, , НОД(ОКА, 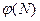 )=1 )=1
| (6.11) |
4. Секретный ключ СКA находится по сформированному открытому ключу так, что
СКА×ОКАº1 (mod 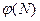 )
или
СКА=ОКА-1 (mod (P-1) × (Q-1)) )
или
СКА=ОКА-1 (mod (P-1) × (Q-1))
| (6.12.) |
Пользователь A может легко найти СКА, используя расширенный алгоритм Евклида, зная числа P и Q, а значит и 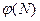 .
.
Любой другой пользователь не может, зная открытый ключ ОКА вычислить СКА, так как ему не известны числа P и Q. Для их нахождения ему потребуется факторизовать известное ему число N, что является вычислительно сложной задачей.
Шифрование и дешифрование сообщений в криптосистеме RSA
Для того, чтобы зашифровать открытое сообщение M, отправитель B должен возвести его в степень открытого ключа пользователя А по модулю N. То есть шифрование выполняется в соответствие с формулой (6.13.).
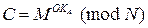
| (6.13.) |
Обращение данной функции, то есть определение значения M по известным значениям С, ОКА, N практически не осуществимо при больших N ( 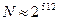 ).
).
Однако знание секретного ключа СКА позволяет обратить данную функцию, то есть решить задачу дешифровки криптограммы C. Для дешифровки криптограммы С необходимо возвести ее в степень секретного ключа пользователя А по модулю N. Таким образом, дешифрование сообщения выполняется в соответствие с формулой (6.14.).
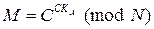
| (6.14.) |
Действительно,
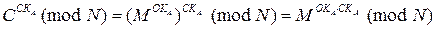
В теории чисел известна теорема Эйлера, утверждающая, что если НОД(x,N)=1, то 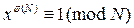 .
.
Согласно 5.12, СКА×ОКАº1 (mod 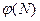 ), то есть СКА×ОКА=k×
), то есть СКА×ОКА=k× 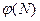 +1. Таким образом,
+1. Таким образом,
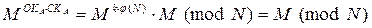
Таким образом, показано, что 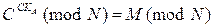 .
.
Получатель А, который создает ключевую пару (ОКА,СКА) защищает два параметра: 1) секретный ключ СКА; 2) пару чисел P и Q. Рассекречивание данных чисел приводит к тому, что злоумышленник сможет вычислить 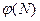 , а значит и вычислить секретный ключ СКА согласно (6.12).
, а значит и вычислить секретный ключ СКА согласно (6.12).
Открытыми в криптосистеме RSA являются только значения ОКА и N.
В настоящее время разработчики криптоалгоритмов с открытым ключом на базе RSA предлагают применять в качестве чисел P,Q,N – числа длиной не менее 200-300 десятичных разрядов.
Пример 6.11.
Зашифруем сообщение DAC по алгоритму RSA. Для простоты вычислений будем оперировать с небольшими числами P и Q.
Действия получателя А
1. Выберем P = 5 и Q = 13
2. Модуль 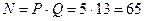
3. 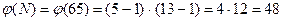
4. В качестве ОКА необходимо выбрать значение, удовлетворяющее условиям 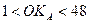 ,
, 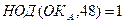 . Пусть ОКА = 5.
. Пусть ОКА = 5.
5. Необходимо найти СКА, такой что 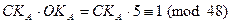 . Это СКА=29. Действительно,
. Это СКА=29. Действительно, 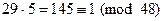 .
.
6. Отправляем пользователю B пару чисел (N=65, ОКА=5)
Действия отправителя B
1. Представим отправляемое сообщение в виде последовательности целых чисел от 0 до 63. Присвоим букве А номер 1, букве B – 2, С – 3, D – 4 и т.д. Тогда открытый текст DAC запишется в виде последовательности чисел 413, то есть M1=4, M2=1, M3=3.
2. Сформируем шифротекст по формуле 6.13.:
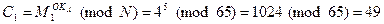 ,
,
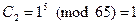 ,
,
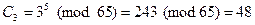 .
.
3. Пользователь B отправляет A криптограмму C1, C2, C3=49, 1, 48.
Действия пользователя A
1. Раскрываем шифротекст по формуле 6.14.:
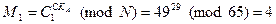 ,
,
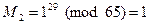 ,
,
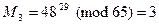 .
.
Таким образом, восстановлено исходное сообщение M1=4=D, M2=1=A, M3=3=C. Исходное сообщение – DAC.
6.6. Выводы
Методы криптографической защиты информации являются основным методом защиты информации от нарушения свойства конфиденциальности.
Выделяют два основных класса криптографических систем - симметричные и асимметричные. Системы первого класса используют для шифрования и дешифрования информации один ключ. Системы второго класса используют ключевую пару, состоящую из открытого ключа и секретно ключа.
Сертифицированным криптографическим алгоритмом в России является симметричный алгоритм ГОСТ 28147-89. Данный алгоритм обязателен для организаций, предприятий и учреждений, применяющих криптографическую защиту данных, относящихся к государственной тайне, хранимых и передаваемых в сетях ЭВМ и в отдельных вычислительных комплексах.
6.7. Вопросы для самоконтроля
1. Что понимают под криптографией?
2. Дайте определение ключа шифрования.
3. Что понимают под криптоанализом?
4. Приведите примеры криптоаналитических атак. Кратко охарактеризуйте их.
5. Какие требования предъявляются к стойким шифрам, используемым для криптографической защиты информации?
6. Сформулируйте закон Керхоффа.
7. Охарактеризуйте подход к криптографической защите, используемый в симметричных криптосистемах.
8. Перечислите недостатки симметричных криптосистем.
9. Охарактеризуйте шифры замены.
10. В чем отличие методов моноалфавитной замены от методов многоалфавитной замены? Приведите примеры шифров каждого из этих классов.
11. Опишите подход к шифрованию, используемый в шифре Цезаря.
12. В чем заключается разница между шифром Цезаря и простой моноалфавитной заменой?
13. В чем заключаются сходство и различие шифров Цезаря, Гронсфельда и Вижинера. Попарно сравните данные шифры.
14. Опишите подход к криптографической защите, используемый в шифре Вернама? В чем его недостатки?
15. В чем заключается шифрование методами перестановки?
16. Опишите подход к шифрованию методами перестановки, основанный на маршрутах Гамильтона.
17. В чем заключается подход к шифрованию методом гаммирования?
18. Дайте определение гаммы шифра.
19. Что является ключом шифрования в шифрах гаммирования?
20. Опишите линейный конгруэнтный метод формирования псевдослучайных последовательностей.
21. Как выполняется криптоанализ, основанный на исследовании частотности символов в тексте?
22. Приведите примеры симметричных алгоритмов шифрования.
23. Опишите схему шифрования информации в алгоритме DES. Какие основные этапы включает данный алгоритм?
24. Каков размер ключа шифрования алгоритма DES?
25. Охарактеризуйте основные режимы шифрования алгоритма DES.
26. Перечислите режимы работы Российского стандарта симметричного шифрования ГОСТ 28147-89.
27. Что понимают под таблицей замен и узлом замены в ГОСТ 28147-89?
28. В чем заключается отличие асимметричных криптосистем от симметричных?
29. Что собой представляет ключевая пара?
30. Охарактеризуйте подход к криптографической защите, используемый в асимметричных криптосистемах.
31. На каком из ключей происходит шифрование информации в асимметричных криптосистемах, а на каком дешифрование?
32. Перечислите требования Диффи-Хеллмана к реализации асимметричных криптосистем.
33. Дайте определение однонаправленной функции и однонаправленной функции с «потайным входом».
34. Приведите примеры однонаправленных функций.
35. Приведите примеры асимметричных алгоритмов шифрования.
36. Опишите схему формирования открытого и закрытого ключей в алгоритме шифрования RSA.
37. Опишите схему шифрования и дешифрования информации в алгоритме RSA.
38. Приведите несколько примеров ключевых пар RSA.
Дата добавления: 2020-10-14; просмотров: 1083;











