Лекция 16. Методы модуляции и сжатия данных
В модемах для телефонных каналов, как правило, используются три вида модуляции:
- частотная;
- относительная фазовая;
- квадратурная амплитудная.
Частотная модуляция весьма помехоустойчива, но при ЧМ неэкономно используется ресурс полосы частот канала. В связи с этим ЧМ применяется в низкоскоростных протоколах, позволяющих осуществлять связь по каналам с низким отношением сигнал/шум.
При использовании ОФМ чаще других видов используется ОФМ-4 или двукратная ОФМ (ДОФМ).
Применение многопозиционной КАМ в чистом виде сопряжено с недостаточной помехоустойчивостью. Поэтому в современных модемах КАМ используется совместно со сверточным кодированием и декодированием Витерби.
Согласованные определенным образом варианты многопозиционной КАМ и сврточного кода, обеспечивающие улучшение энергетической и частотной эффективности называются сигнально-кодовыми конструкциями (СКК) или треллис-модуляцией. СКК позволяют повысить помехозащищенность передачи информации наряду со снижением требований к отношению сигнал/шум в канале на 3-6 дБ. При этом число точек в сигнальном созвездии увеличивается вдвое за счет добавления к информационным битам одного избыточного, образованного путем сверточного кодирования. Задача поиска наилучшей СКК является одной из наиболее сложных задач теории связи. Современные высокоскоростные протоколы (V.32, V.32 bis, V.34 и др.) предполагают обязательное применение СКК.
Как известно,применениесжатия данных позволяет более эффективно использовать емкость дисковой памяти (архиваторы). Не менее полезно применение сжатия данных при передаче информации в любых системах связи. В этом случае появляется возможность передавать значительно меньшие объемы данных и, следовательно, требуются значительно меньшие ресурсы пропускной способности каналов для передачи той же самой информации.
Теоретической предпосылкой возможности сжатия данных выступает известная из теории информации теорема Шеннона. Она утверждает, что в канале без помех можно так преобразовать последовательность символов источника в последовательность символов кода, что средняя длина символов кода может быть сколь угодно близкой к энтропии источника сообщений H(X). Понятие энтропии источника сообщений также введено Шенноном.
Она определяется в соответствии с выражением
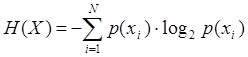 ,
,
где p(xi) – вероятность появления конкретного сообщения или символа xi из N возможных символов алфавита источника. N называется объемом алфавита источника. Энтропия источника H(X) выступает количественной мерой разнообразия выдаваемых источником символов или мерой априорной неопределенности выдачи конкретного символа xi из множества возможных. Чем выше разнообразие алфавита символов источника и порядка их выдачи, тем больше энтропия H(X) и тем сложнее эту последовательность символов сжать.
Энтропия максимальна 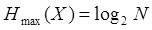 , если символы выдаются источником независимо друг от друга и с равной вероятностью. С другой стороны, H(X) =0, если один из символов выдается постоянно, а появление других невозможно. Единицей измерения энтропии является бит. 1 бит – это та неопределенность, которую имеет источник с равновероятной выдачей двух возможных символов.
, если символы выдаются источником независимо друг от друга и с равной вероятностью. С другой стороны, H(X) =0, если один из символов выдается постоянно, а появление других невозможно. Единицей измерения энтропии является бит. 1 бит – это та неопределенность, которую имеет источник с равновероятной выдачей двух возможных символов.
Энтропия источника H(X) определяет среднее число двоичных символов, необходимых для кодирования символов источника. Так, если символами источника являются буквы русского алфавита (N=32), они передаются равновероятно и независимо друг от друга, то 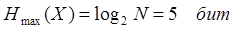 , то есть каждую букву алфавита можно закодировать последовательностью из пяти двоичных символов.
, то есть каждую букву алфавита можно закодировать последовательностью из пяти двоичных символов.
Если символы выдаются источником не с равной вероятностью и не независимо, то энтропия источника 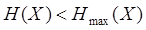 . В этом случае возможно более экономное кодирование. На каждый символ источника может быть затрачено в среднем
. В этом случае возможно более экономное кодирование. На каждый символ источника может быть затрачено в среднем 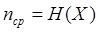 символов кода. Для характеристики достижимой или потенциально возможной степени сжатия используется коэффициент избыточности:
символов кода. Для характеристики достижимой или потенциально возможной степени сжатия используется коэффициент избыточности:
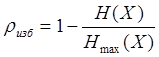 .
.
Для характеристики достигнутой на практике степени сжатия применяют коэффициент сжатия, под которым понимают отношение первоначального объема данных к их объему в сжатом виде.
В качестве примера, поясняющего принцип сжатия, можно привести методы, используемые для построения кодов, называемых эффективными. В чистом виде в современных системах передачи данных они не применяются, однако позволяют проиллюстрировать принципы, заложенные в более эффективных и сложных методах.
Целью эффективного кодирования является устранение избыточности сообщений, поскольку избыточные сообщения требуют большего времени для передачи и большего объема памяти для хранения.
Очевидно, что для уменьшения избыточности кодовых комбинаций, кодирующих символы сообщений, необходимо выбирать максимально короткие кодовые комбинации. Однако для полного устранения избыточности этого недостаточно. При кодировании необходимо учитывать вероятности появления каждого символа в сообщениях и наиболее вероятным символам сопоставлять короткие кодовые комбинации, а наименее вероятным – более длинные.
В качестве иллюстрации – простой пример. Пусть сообщение может состоять из двух слов. Длина первого - один кодовый символ, второго - три кодовых символа. Вероятности появления слов в сообщении соответственно 0,1 и 0,9. Тогда статистически средняя длина слова в сообщении 1*0,1 + 3*0,9 = 2,8 символа. Если слова будут иметь другие вероятности, например, 0,9 и 0,1, то средняя длина слова составит 1*0,9 + 3*0,1 = 1,2 символа. Отсюда видно, что длина кодовой комбинации должна выбираться в зависимости от вероятности появления кодируемого этой комбинацией символа сообщения. Чем чаще он появляется, т.е. чем больше его вероятность, тем более короткую кодовую комбинацию ему следует сопоставить.
Формализуем задачу эффективного кодирования. Пусть входным алфавитом кодирующего отображения является множество сообщений 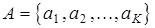 . Пусть выходным алфавитом кодирующего отображения будет множество В , число элементов которого равно m .Кодирующее отображение сопоставляет каждому сообщению аi кодовую комбинацию, составленную из ni символов алфавита В . Требуется оценить минимальную среднюю длину кодовой комбинации. Сравнивая ее со средней длиной кодовой комбинации, вычисленной для какого-либо конкретного кода, можно оценить, насколько данный конкретный код находится близко к эффективному, т.е. безизбыточному коду.
. Пусть выходным алфавитом кодирующего отображения будет множество В , число элементов которого равно m .Кодирующее отображение сопоставляет каждому сообщению аi кодовую комбинацию, составленную из ni символов алфавита В . Требуется оценить минимальную среднюю длину кодовой комбинации. Сравнивая ее со средней длиной кодовой комбинации, вычисленной для какого-либо конкретного кода, можно оценить, насколько данный конкретный код находится близко к эффективному, т.е. безизбыточному коду.
Энтропия сообщения А по определению
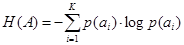 . .
| (4.1) |
Средняя длина кодовой комбинации
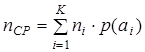 , ,
| (4.2) |
где ni - длина кодовой комбинации, сопоставленной сообщению аi. Максимальная энтропия, которую может иметь сообщение из nСР символов алфавита В, число элементов которого равно m , равна
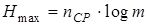 . .
| (4.3) |
Очевидно, что для обеспечения передачи информации, содержащейся в сообщении А, с помощью кодовых комбинаций алфавита В должно выполняться неравенство
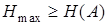
| (4.4) |
или с учетом (4.3) 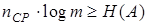 или с учетом (4.1)
или с учетом (4.1)
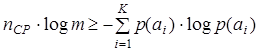 . .
| (4.5) |
При строгом неравенстве (4.4) закодированное сообщение обладает избыточностью, т.е. для кодирования используется больше символов, чем это минимально необходимо. Для числовой оценки избыточности в предыдущей главе использовался коэффициент избыточности
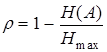 . .
| (4.6) |
Поскольку из (4.3) и (4.4) следует, что 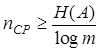 , то ясно, что
, то ясно, что
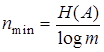 . .
| (4.7) |
Тогда формулу (4.6) для коэффициента избыточности для кода можно переписать в следующем виде
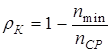 . .
| (4.8) |
Под эффективным кодом понимается код, rК которого равен 0, т.е. для абсолютно эффективных кодов 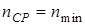 . Тогда и неравенство (4.5) переходит в равенство
. Тогда и неравенство (4.5) переходит в равенство 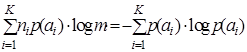 , откуда
, откуда 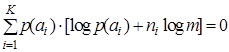 .
.
Предположив очевидное, что А не содержит элементов с p(ai) = 0, получим
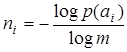
| (4.9) |
для всех i. Но отношение (4.9) не всегда дает целочисленный результат. Следовательно, не для любого набора А с заданным распределением вероятностей p(ai) можно построить абсолютно эффективный код с rК = 0. Тем не менее, всегда можно обеспечить выполнение неравенства 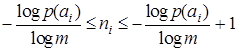 , умножая которое на p(ai) и суммируя по i , получим
, умножая которое на p(ai) и суммируя по i , получим
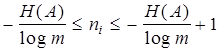 . .
| (4.10) |
Неравенство (4.10) может служить критерием для оценки эффективности какого-либо конкретного кода.
Для построения эффективных кодов используются различные алгоритмы. Одним из них является код Шеннона – Фано. Код Шеннона – Фано строится следующим образом. Символы алфавита источника выписываются в порядке убывания их вероятностей. Затем вся совокупность разделяется на две группы так, чтобы суммы вероятностей в каждой из групп были по возможности одинаковыми. Далее всем символам одной группы в качестве первого кодового символа приписывается 1, а другой группы – 0. Далее каждая из полученных групп в свою очередь разбивается на две подгруппы с одинаковыми суммарными вероятностями и т.д. Процесс повторяется до тех пор, пока в каждой группе останется по одному символу.
Пример 4.1. Закодировать двоичным кодом Шеннона – Фано ансамбль {ai} (i=1,2,...,8), если вероятности символов ai имеют следующие значения
| ai | a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 |
| pi | 0,25 | 0,25 | 0,125 | 0,125 | 0,0625 | 0,0625 | 0,0625 | 0,0625 |
Найти среднее число символов в кодовой комбинации и коэффициент избыточности кода.
Решение.
| ai | pi | кодовая комбинация | ni | pini | H(ai) |
| a1 | 0,25 | 11 | 2 | 0,5 | 0,5 |
| a2 | 0,25 | 10 | 2 | 0,5 | 0,5 |
| a3 | 0,125 | 011 | 3 | 0,375 | 0,375 |
| a4 | 0,125 | 010 | 3 | 0,375 | 0,375 |
| a5 | 0,0625 | 0011 | 4 | 0,25 | 0,25 |
| a6 | 0,0625 | 0010 | 4 | 0,25 | 0,25 |
| a7 | 0,0625 | 0001 | 4 | 0,25 | 0,25 |
| a8 | 0,0625 | 0000 | 4 | 0,25 | 0,25 |
По формуле (4.2) 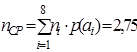 , по формуле (4.1)
, по формуле (4.1) 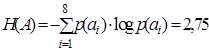 , тогда по формуле (4.7)
, тогда по формуле (4.7) 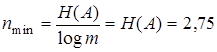 и по формуле (4.8)
и по формуле (4.8) 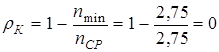 , таким образом, построен абсолютно эффективный код.
, таким образом, построен абсолютно эффективный код.
Алгоритм кодирования Шеннона – Фано имеет простую графическую иллюстрацию в виде графа, называемого кодовым деревом. Граф для кода Шеннона – Фано строится следующим образом. Из нижней или корневой вершины графа исходят два ребра, одно из которых помечается символом 0, а другое – 1. Эти два ребра соответствуют разбиению множества символов алфавита источника на две примерно равновероятные группы, одной из которых сопоставляется кодовый символ 0, а другой – 1. Ребра, исходящие из вершин следующего уровня, соответствуют разбиению получившихся групп на равновероятные подгруппы и т.д. Построение графа заканчивается, когда множество символов алфавита источника будет разбито на одноэлементные подмножества. Каждая концевая вершина графа, т.е. вершина, из которой уже не исходят ребра, соответствует некоторой кодовой комбинации. Чтобы сформировать эту комбинацию, надо пройти путь от корневой вершины до соответствующей концевой, выписывая в порядке следования по этому пути кодовые символы с ребер пути.
Рассмотренная методика Шеннона – Фано не всегда приводит к однозначному построению кода, поскольку в зависимости от вероятностей отдельных символов можно несколькими способами осуществить разбиение на группы.
Пример 4.2. Закодировать двоичным кодом Шеннона – Фано ансамбль {ai} (i=1,2,...,8), если вероятности символов ai имеют следующие значения
| ai | a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 |
| pi | 0,22 | 0,20 | 0,16 | 0,16 | 0,10 | 0,10 | 0,04 | 0,02 |
Найти коэффициент избыточности кода.
Решение.1
| ai | pi | кодовая комбинация | ni | pini | H(ai) |
| a1 | 0,22 | 11 | 2 | 0,44 | 0,4806 |
| a2 | 0,20 | 101 | 3 | 0,6 | 0,4643 |
| a3 | 0,16 | 100 | 3 | 0,48 | 0,4230 |
| a4 | 0,16 | 01 | 2 | 0,32 | 0,4230 |
| a5 | 0,10 | 001 | 3 | 0,30 | 0,3322 |
| a6 | 0,10 | 0001 | 4 | 0,40 | 0,3322 |
| a7 | 0,04 | 00001 | 5 | 0,20 | 0,1857 |
| a8 | 0,02 | 00000 | 5 | 0,10 | 0,1129 |
По формуле(4.2) 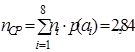 , по формуле (4.1)
, по формуле (4.1) 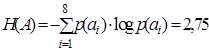 , тогда по формуле (4.7)
, тогда по формуле (4.7) 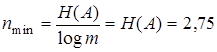 и по формуле (4.8)
и по формуле (4.8) 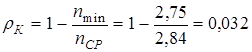 ..
..
Решение.2
| ai | pi | кодовая комбинация | ni | pini | H(ai) |
| a1 | 0,22 | 11 | 2 | 0,44 | 0,4806 |
| a2 | 0,20 | 10 | 2 | 0,40 | 0,4643 |
| a3 | 0,16 | 011 | 3 | 0,48 | 0,4230 |
| a4 | 0,16 | 010 | 3 | 0,48 | 0,4230 |
| a5 | 0,10 | 001 | 3 | 0,30 | 0,3322 |
| a6 | 0,10 | 0001 | 4 | 0,40 | 0,3322 |
| a7 | 0,04 | 00001 | 5 | 0,20 | 0,1857 |
| a8 | 0,02 | 00000 | 5 | 0,10 | 0,1129 |
По формуле(4.2) 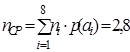 , по формуле (4.1)
, по формуле (4.1) 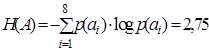 , тогда по формуле (4.7)
, тогда по формуле (4.7) 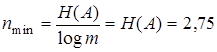 и по формуле (4.8)
и по формуле (4.8) 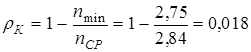 , т.е. второй вариант решения ближе к оптимальному, поскольку обеспечивает меньший коэффициент избыточности.
, т.е. второй вариант решения ближе к оптимальному, поскольку обеспечивает меньший коэффициент избыточности.
От данной неоднозначности построения эффективного кода свободен код Хаффмена. Для двоичного кода методика Хаффмена сводится к следующему. Символы алфавита источника выписываются в основной столбец таблицы в порядке убывания вероятностей. Далее два последних символа объединяются в один вспомогательный с вероятностью, равной сумме вероятностей объединяемых символов. Вероятности символов, не участвовавших в объединении, и полученная суммарная вероятность снова располагаются в порядке убывания в дополнительном столбце таблицы, после чего два последних символа вновь объединяются. Процесс повторяется до тех пор, пока не буде получен единственный вспомогательный символ с вероятностью, равной 1. Для составления кодовых комбинаций, соответствующих символам, необходимо проследить пути переходов по строкам и столбцам таблицы.
Для наглядного представления этого процесса удобнее всего построить граф, называемый кодовым деревом. Процедура построения кодового дерева выглядит следующим образом. Из вершины, соответствующей последнему единственному вспомогательному символу с вероятностью, равной 1, направляются две ветви, причем ветви с большей вероятностью присваивается кодовый символ 1, а с меньшей – 0. Такое последовательное ветвление из вершин, соответствующих вспомогательным символам, продолжается до получения вершин, соответствующих основным исходным символам.
Пример 4.3. Закодировать двоичным кодом Хаффмена ансамбль из примера 4.2. Решение представлено на рис. 4.12.
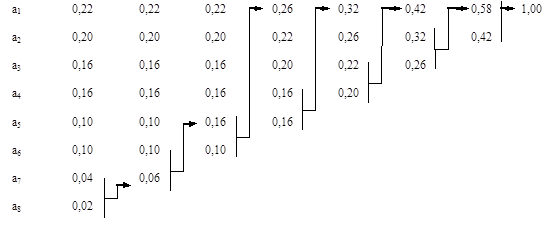
|
| Рисунок 4.12. Кодирование методом Хаффмена |
Кодовое дерево для этого примера изображено на рис. 4.13
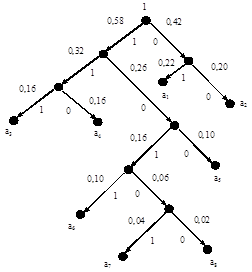 Рисунок 4.13. Кодовое дерево
Рисунок 4.13. Кодовое дерево
| Составленная в соответствии с графом таблица кодовых комбинаций
|
Таким образом, получены те же параметры в смысле избыточности, что и в примере 4.2, решение 2 для кода Шеннона – Фано, хотя кодовые комбинации по составу другие.
Из рассмотрения методов построения эффективных кодов следует, что эффект уменьшения избыточности достигается за счет различия в числе разрядов в кодовых комбинациях, т.е. эти эффективные коды являются неравномерными, а это приводит к дополнительным трудностям при декодировании. Как вариант, можно для различения кодовых комбинаций ставить специальный разделительный символ, но при этом снижается эффект, т.к. средняя длина кодовой комбинации увеличивается на один разряд.
Более целесообразно обеспечить однозначное декодирование без введения дополнительных разрядов. Для этого эффективный код необходимо строить так, чтобы ни одна комбинация кода не совпадала с началом другой более длинной кодовой комбинации. Коды, удовлетворяющие этому условию, называются префиксными.
Наличие или отсутствие свойства префиксности отражается и на кодовом дереве. Если свойство префиксности отсутствует, то некоторые промежуточные вершины кодового дерева могут соответствовать кодовым комбинациям.
Префиксные коды иногда называют мгновенно декодируемыми, поскольку конец кодовой комбинации опознается сразу, как только мы достигаем конечного символа кодовой комбинации при чтении кодовой последовательности. В этом состоит преимущество префиксных кодов перед другими однозначно декодируемыми неравномерными кодами, для которых конец каждой кодовой комбинации может быть найден лишь после анализа одной или нескольких последующих комбинаций, а иногда и всей последовательности. Это приводит к тому, что декодирование осуществляется с запаздыванием по отношению к приему последовательности.
Очевидно, что практическое применение могут иметь только префиксные коды. Коды Шеннона – Фэно и Хаффмена являются префиксными.
Рассмотренные вопросы исследуются в лабораторной работе №9 «Методы эффективного кодирования» [1. с. 86-97].
При использовании префиксных кодов возникает вопрос о том, каковы возможные длины кодовых комбинаций префиксного кода. Пусть a1, a2, . . . , aN - кодовые комбинации префиксного двоичного кода. Пусть nk -число кодовых комбинаций длины k . Число nk совпадает с числом вершин k-го уровня кодового дерева. Конечно справедливо неравенство nk £ 2k, поскольку 2k - максимально возможное число вершин на k-м уровне двоичного дерева. Однако для префиксного кода можно получить гораздо более точную оценку. Если n1, n2, . . . , nk-1 - число вершин 1-го, 2-го, . . . , (k-1)-го уровней дерева, то число всех вершин k-го уровня кодового дерева префиксного кода равно 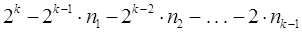 , и поэтому
, и поэтому 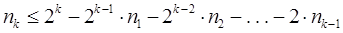 , или иначе
, или иначе 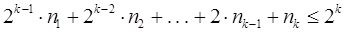 .
.
Деля обе части неравенства на 2k,получим 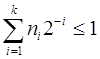 . Это неравенство справедливо для любого k£L , где L - максимальная длина кодовых комбинаций
. Это неравенство справедливо для любого k£L , где L - максимальная длина кодовых комбинаций 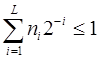 . Если обозначить l1, l2, . . . , lN длины кодовых комбинаций a1, a2, . . . , aN , то последнее неравенство можно записать следующим образом
. Если обозначить l1, l2, . . . , lN длины кодовых комбинаций a1, a2, . . . , aN , то последнее неравенство можно записать следующим образом 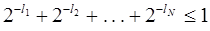 .
.
Это и есть условие, которому должны удовлетворять длины кодовых комбинаций двоичного префиксного кода. Это неравенство в теории кодирования называется неравенством Крафта и является достаточным условием того, что существует префиксный код с длинами кодовых комбинаций l1, l2, . . . , lN .
Если кодовый алфавит содержит не два, а S символов, то подобным же образом доказывается, что необходимым и достаточным условием для существования префиксного кода является выполнение неравенства 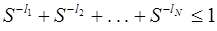 .
.
Эффективное кодирование направлено на устранение избыточности, вызванной неравной априорной вероятностью символов источника. Устранение избыточности, обусловленной наличием корреляции между символами, основано на переходе от кодирования отдельных символов источника к кодированию групп этих символов, то есть происходит укрупнение алфавита источника.
Общая избыточность при укрупнении алфавита не изменяется. Это вызвано тем, что уменьшение избыточности, обусловленной взаимными связями между символами, сопровождается соответствующим возрастанием избыточности, обусловленной неравномерностью появления различных групп символов, то есть символов нового укрупненного алфавита. Таким образом, происходит конвертация одного вида избыточности в другой.
Сжатие бывает с потерями и без потерь при восстановлении. В системах передачи данных используются только методы сжатия без потерь.
Эти методы подразделяются на несколько основных групп:
1. Кодирование повторов. Суть метода состоит в замене последовательности одинаковых повторяющихся символов на один такой символ и число, соответствующее количеству его повторений.
2. Вероятностные методы сжатия. Основу этих методов составляют алгоритмы Шеннона – Фано и Хаффмена. Существуют две разновидности вероятностных методов, различающихся способом определения вероятности появления каждого символа:
а) статические, использующие фиксированную таблицу частоты появления символов, рассчитываемую перед началом процесса сжатия. Статические методы характеризуются хорошим быстродействием и не требуют значительных ресурсов оперативной памяти. Они нашли широкое применение в различных программах- архиваторах, но для сжатия данных, передаваемых модемами, используются редко, поскольку в них предпочтение отдается методам словарей, обеспечивающим большую степень сжатия.;
б) динамические или адаптивные, в которых частота появления символов все время меняется и по мере считывания нового блока данных происходит перерасчет начальных значений частот символов.
Комбинация методов кодирования повторов и адаптивного кодирования с применением кода Хаффмена используется в протоколе MNP5. На перовом этапе процедуры сжатия в соответствии с этим протоколом каждая группа из трех и более (до 253) одинаковых смежных символов преобразуется к виду символ и число символов. На втором этапе используется адаптивное кодирование с применением кода Хаффмена. В протоколе MNP5 определяются 256 лексем для всех возможных 8-разрядных величин – октетов. Лексема состоит из трехразрядного префикса и суффикса, который может включать от 1 до 8 разрядов. Как приемник, так и передатчик инициализируют исходные символьно-лексемные таблицы. После того, как обработан каждый октет передаваемого сообщения, таблица передатчика переопределяется, исходя из частоты появления каждого октета. Октетам, которые появляются чаще, ставятся в соответствие наиболее короткие лексемы. На приемном конце лексемы преобразуются в октеты. В соответствии с частотой появления тех или иных октетов трансформируется символьно-лексемная таблица приемника. Тем самым осуществляется самосинхронизация таблиц кодирования и декодирования.
Протокол MNP5 обеспечивает степень сжатия в среднем 2:1. Более совершенным протоколом, обеспечивающим степень сжатия до 3:1, является протокол MNP7.
Протокол MNP7 использует улучшенную форму кодирования методом Хаффмена в сочетании с алгоритмом прогнозирования, который может предсказывать следующий символ в последовательности, исходя из появившегося предыдущего символа. Для каждого октета формируется таблица из всех 256 возможных следующих за ним октетов, расположенных в соответствии с частотой их появления. Октет кодируется путем выбора столбца, соответствующего предыдущему октету, с последующим отысканием в этом столбце значения текущего октета. Строка, в которой находится текущий октет, определяет лексему так же, как в MNP5. После того, как каждый октет будет закодирован, порядок следования октетов в выбранном столбце изменяется в соответствии с новыми относительными частотами появления октетов.
3. Метод словарей. Наиболее известным и включенным в рекомендации V.42bis алгоритмом данного типа является алгоритм LZW (Lempel – Ziv – Welch), обеспечивающий коэффициент сжатия 4:1 файлов с оптимальной структурой.
Алгоритм LZW построен на основе словаря или таблицы фраз, которая отображает строки символов сжимаемого сообщения в коды фиксированной длины, равные 12 битам.
Таблица обладает свойством предшествования, т.е. для каждой фразы словаря, состоящей из некоторой фразы w и символа K, фраза w тоже содержится в словаре.
Алгоритм LZW работает следующим образом:
1. Инициализировать словарь односимвольными фразами, соответствующими символам входного алфавита. Прочитать первый символ сообщения в текущую фразу w. Текущей фразой на первом шаге алгоритма является пустая фраза.
2. Прочитать очередной символ сообщения K. Если это символ конца сообщения, то выдать код w и закончить работу алгоритма. Если нет, перейти к п.3.
3. Если фраза w K уже есть в словаре, то заменить w на код фразы w K и перейти к п.2.
4. Если фразы w K нет в словаре, то выдать код w в линию и добавить w K в словарь, после чего повторить п.2.
Декодер LZW должен использовать тот же словарь, что и кодер, строя его по аналогичным правилам при восстановлении сжатых данных. Каждый считываемый код разбирается с помощью словаря на предшествующую фразу w и символ K. Затем рекурсия продолжается для предшествующей фразы w до тех пор, пока она не окажется кодом одного символа. При этом завершается декомпрессия этого кода. Обновление словаря происходит для каждого декодируемого кода, кроме первого. После завершения декодирования кода его последний символ, соединенный с предыдущей фразой, добавляется в словарь. Новая фраза получает то же значение кода т.е. позицию в словаре, что присвоил ей кодер. В результате такого процесса, шаг за щагом декодер восстанавливает тот словарь, что построил кодер. Декодирование в алгоритме LZWобычно намного быстрее процесса кодирования.
К параметрам алгоритма, значения которых могут быть согласованы между взаимодействующими модемами, относятся:
- максимальный размер выходного кодового слова;
- общее число кодовых слов;
- размер символа;
- число символов в алфавите;
- максимальная длина последовательности символов.
Кроме того, алгоритм осуществляет мониторинг входного и выходного потоков данных для определения эффективности сжатия. Если сжатия не происходит или оно невозможно в силу природы передаваемых данных, алгоритм прекращает свою работу. Это свойство обеспечивает лучшие рабочие характеристики при передаче файлов, которые уже были сжаты, например, заархивированы, или которые не поддаются сжатию.
Контрольные вопросы к лекции 16
16-1. Что называется сигнально-кодовой конструкцией?
16-2. Что называется энтропией источника сообщений?
16-3. Когда энтропия источника максимальна?
16-4. Когда энтропия источника минимальна?
16-5. В чем состоит суть эффективного кодирования по методу Шеннона – Фано?
16-6. Как строится эффективный код по методу Шеннона – Фано?
16-7. В чем состоит недостаток эффективного кодирования по методу Шеннона – Фано?
16-8. Как строится эффективный код по методу Хаффмена?
16-9. Какие эффективные коды называются префиксными?
16-10. Почему при укрупнении алфавита общая избыточность не меняется?
16-11. Перечислите основные методы сжатия информации без потерь.
16-12. В чем состоит суть метода кодирования повторов?
16-13. Чем статические вероятностные методы сжатия отличаются от динамических?
16-14. Чем протокол сжатия MNP7 отличается от протокола MNP5?
16-15. Что означает свойство предшествования таблицы фраз в алгоритме LZW?
16-16. Какие параметры алгоритма LZW согласовываются между взаимодействующими пользователями?
16-17. С какой целью алгоритм LZW осуществляет мониторинг входного и выходного потоков данных?
Дата добавления: 2020-10-14; просмотров: 677;











