Конъюнкции и дизъюнкции над множеством переменных. Нормальные формы

Определение.Конъюнкцией над множеством переменных Х=(х₁,... ,х_n) называется логическое произведение вида:

К= х_i₁^aⁱ¹& . . . & х_is^a^is ,

где (х_i_{1 , ... ,}х_is) Í Х, х_ik^a^ik = x_ikлибо`x_ik.

Конъюнкцию К можно представить как результат (s-1)применения двуместной функции логического умножения либо одной обобщенной функции &, а также одноместной функции Ø . Аналогом функции & по принципу действия (выделение 1 на крайней позиции вектора истинности) является функция Вебба¯. Поскольку правило x& у=`x ¯ у справедливо для любого числа переменных, то любая конъюнкция Кможет быть представлена в виде: К=¯( х_i1^Ø^aⁱ¹, . . . , х_is^Ø^aⁱ ^s ), где ¯ ― обобщенная функция Вебба. Данное представление назовем представлением в базисном наборе(Ø, ¯). Отрицание`x может быть выражено при помощи функции Вебба следующими способами:`x = ¯(х, х) = ¯(х, 0) =¯(0, х ) (дублирующая подстановка (х, х) на практике реализуется замыканием входов элемента ¯ , а подстановка 0 ― заземлением соответствующего входа у функционального элемента (рис.1.5)). Поэтому любая конъюнкция Кможет быть полностью выражена при помощи элементов ¯ ( в базисном наборе(¯)). При этом общее число функциональных элементов в конъюнкции Кпри использовании обоих базисных наборов одинаково.

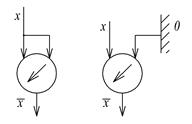
Рис.1.5

Определение. Дизъюнкцией над множеством переменных Х=(х₁, ... , х_n)называется логическая сумма вида:

D= х_i₁^aⁱ¹Ú. . . Ú х_is ^a^is,

где (х_i_{1, ... ,}х_is ) Í Х, х_ik^a^ik = x_ik либо`x_ik .

Дизъюнкция D может быть реализована как при помощи (s-1)двуместной функции Ú, так и применением одной обобщенной функции Ú, а также одноместной функции Ø. Поскольку аналогом функции Úпо принципу действия (выделение 0 на крайней позиции вектора истинности) является функция штрих Шеффера |, то с учетом зависимости xÚ у =`x |` у, любая дизъюнкция D может быть представлена в виде:

D = | ( х_i₁^Ø^aⁱ¹, . . . , х_is^Ø^a^is ),

где | ― обобщенная функция Шеффера. Данное представление назовем представлением в базисном наборе(Ø, | ).

Так как отрицание можно выразить через | :`x =| (х, х) = | (х,1) = |(1,х)(рис.1.6), то с использованием данных правил любая дизъюнкция D может быть полностью выражена при помощи элементов| ( в базисном наборе( | )). При этом у одной и той же дизъюнкции общее число функциональных символов при использовании обоих наборов также одинаково.

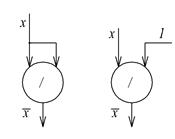
Рис.1.6

Определение. Дизъюнктивной нормальной формой (ДНФ) булевой функции f (х ⁿ)называется формульное выражение вида:

f = К₁Ú ... Ú К_р ,

где К₁ , ... , К_р- конъюнкции.

Для соединения конъюнкций в ДНФ могут использоваться как 2—местная, так и обобщенная функция Ú. Последняя с использованием эквивалентного соотношения

Ú (К₁ , ... , К_р) = Ø ¯ ( К₁ , ... , К_р)

может быть заменена обобщенной функцией Вебба.

Определение. Веббовой нормальной формой (ВНФ) булевой функции f (`х ⁿ)назовем её выражение вида:

f = Ø ¯ ( К₁ , ... , К_р),

где К₁,...,К_р— конъюнкции, представленные как К_s =¯( х_i₁^Ø^aⁱ¹, ... , х_is^Ø^a^is), (1£ s £ p).

С помощью ДНФ и ВНФ наиболее просто выражаются булевы функции, у которых в векторе истинности преобладают нули и мало единиц.

Замечание 1. В виде ДНФ и ВНФ могут быть представлены все функции алгебры логики, не равные константе 0. Эта функция не представима в данных формах, поскольку при наличии хотя бы одной конъюнкции в формулах ДНФ или ВНФ в векторе истинности функции также должна присутствовать хотя бы одна единица.

Замечание 2. Выражения с одним слагаемым вида f = К₁для сохранения общности также будем относить к ДНФ (ВНФ). Назовем такие формы вырожденными.

Пример 1. Представить ДНФ булевой функции f = х`у Ú`х у z в эквивалентной ВНФ. Дать решение задачи а) в базисном наборе(Ø, ¯)и б) в базисном наборе(¯) .

Решение. Заменяя умножение во внутренних конъюнкциях ДНФ функцией Вебба, вначале изменим внутренние конъюнкции формы: х`у = ¯(х, у), `х у z = ¯(х,`у,`z). Внешнее сложение преобразуем с использованием правила: Ú (К₁, ... , К_р) = Ø ¯ (К₁ , ... , К_р). В итоге получим искомое выражение функции в базисном наборе(Ø, ¯):

f = Ø¯ (¯(х, у), ¯(х, у, z )).

Применяя эквивалентную замену`x = ¯(х, х), находим формульное выражение функции, содержащее только функцию Вебба:

f =¯[¯ (¯(¯(х, x), у), ¯( х, ¯(y, у), ¯(z, z))), ¯ (¯(¯(х, x), у), ¯( х, ¯(y, у), ¯(z ,z)))].

Полученные выражения дают искомое решение задачи.

Определение. Конъюнктивной нормальной формой (КНФ) булевой функции f (х ⁿ)называется её формульное выражение вида:

f=D₁&...& D_р,

где D₁ ,..., D_р— дизъюнкции.

В КНФ могут использоваться 2 — местная или обобщенная функции &. Последняя с использованием эквивалентного соотношения & (D₁, ... , D_р) = Ø|(D₁, ... , D_р) может быть заменена обобщенной функцией Шеффера.

Определение. Шефферовой нормальной формой (ШНФ) булевой функции f (х ⁿ)назовем её выражение вида:

f = Ø|(D₁, ..., D_р),

где D₁, ... ,D_р— дизъюнкции, представленные в эквивалентной форме D_i =| (х_i₁^Ø^aⁱ¹, . . . , х_is^Ø^aⁱ ^s ),(1£ i £ p).

Замечание 3. В виде КНФ и ШНФ могут быть представлены все функции алгебры логики, не равные константе 1. Данная функция не представима в виде КНФ и ШНФ, поскольку при наличии хотя бы одной дизъюнкции в их формулах вектор истинности функции также должен иметь хотя бы один нуль.

Замечание 4. Выражения с одним сомножителем вида f = D₁для сохранения общности будем считать вырожденными КНФ (ШНФ).

Пример 2. Перевести КНФ булевой функции f =(`х Ú у Ú z)& (`у Ú z) в эквивалентную ШНФ. Дать решение задачи а) в базисном наборе(Ø, |)и б) в однофункциональном наборе(|) .

Решение. Заменим сложение во внутренних суммах (дизъюнкциях) КНФ обобщенной функцией Шеффера: (х Ú у Ú z) = | (х,`у,`z); (у Ú` z)= | (у, z). Затем по правилу & (D₁, ... , D_р)= Ø |(D₁, . . . , D_р)производим замену внешнего сложения. В итоге получаем выражение функции в базисном наборе(Ø, | ):