Минимизация нормальных форм булевых функций

При решении задач анализа и проектирования логических схем основными критериями их оптимальности, как правило, являются минимумы общего числа функциональных или релейных элементов, входящих в них, а также общего числа соединений в схеме. Данная минимизация упрощает последующую физическую реализацию схем, повышает их надежность и в то же время – уменьшает габариты, материалоемкость, себестоимость.

Рассмотрим построение булевых функций, соответствующих логических схемам с данными свойствами.

Определение: Минимальной ДНФ (МДНФ) функции алгебры логики f(хⁿ) называется её ДНФ, содержащая в своей формуле минимально возможное число символов переменных.

Аналогично вводятся понятия минимальных КНФ (МКНФ), минимальных ВНФ (МВНФ), минимальных ШНФ (МШНФ).

Каждую из совершенных нормальных форм произвольной булевой функции f (хⁿ)(СДНФ, СКНФ, СВНФ, СШНФ) можно представить в виде:

f = F(j(x₁^a11 ,..., x_n ^a1n) , ...,j (x₁^ak1,..., x_n ^akn)),

где F — внешняя функция, j (x₁^ai1 ,..., x_n^ain) — внутренняя функция, которая при подстановке переменных (x₁^ai1, ..., x_n^ain)является конституентой нуля либо единицы на одном из наборов значений переменных `хⁿ , т.е. принимает на нем значение нуль (единица) , а на всех других наборах — противоположное значение. В СВНФ и СШНФ внешними являются функции د =Ú и Ø | = & .

Определение. Наборы переменных (x₁^ai1,...,x_n^ain), входящие во внутренние функции jв совершенных нормальных формах, назовем элементарными наборами.

Множество элементарных наборов в рассматриваемой совершенной форме булевой функции будем обозначать через {N} = {N₁, ... , N_k}, где k — число нулей (единиц) в векторе значений исходной функции, равное числу внутренних функций jв форме. Как отмечалось ранее, в совершенных нормальных формах используются только пороговые функции. СДНФ и СВНФ строятся по единичным значениям функции, СКНФ и СШНФ — по нулевым.

В процессе минимизации производится параллельное сокращение:

а) чисел переменных во внутренних функциях j(x₁^ai1 ,..., x_n^ain),

б) числа k самих внутренних функций j(x₁^ai1 ,..., x_n^ain) .

Для характеристики данных сокращений вводятся вспомогательные понятия простых наборов, сокращенных и тупиковых нормальных форм.

Определение. Набор переменных (x₁^ai1,..., x_n^ain), входящий во внутреннюю функцию jединичной (нулевой) нормальной формы булевой функции f (хⁿ ), называют ее простым набором, если при удалении из (x₁^ai1 , ... , x_n^ain) любой переменной x^aiк новая функция j(x₁^ai1, ... ,x_k-1^ai(к-1),x_k+1^ai(к+1), ... ,x_n^ain) получает новые единичные (нулевые) значения в векторе истинности, которых нет у исходной f (х ⁿ).

Множество простых наборов в нормальных формах будем обозначать через {P} = {P₁,...,P_s}, где s — общее число таких наборов.

Пример 1. Рассмотрим функцию f(x,y,z)= (00101100). Необходимо выяснить, какие из её элементарных наборов являются простыми.

Решение. СДНФ имеет вид: f =`x y z Ú x`y`z Ú x`y z.

Элементарные наборы будут следующими:

N₁=(x , y,`z), N<sub>2</sub>= (x,`y,`z), N<sub>3</sub>=(x,`y, z).

Рассмотрим элементарный набор N₁=(x, y,`z)и попробуем удалить из него поочередно каждую из его переменных.

а) Удаление`x приводит к тому, что новая сокращенная конъюнкция у`z будет иметь помимо единицы на наборе (0, 1, 0)дополнительное значение 1 на наборе (1, 1, 0). Но f (1, 1, 0) = 0, поэтому переменную 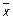из набора удалять нельзя.

б) Удаление у приводит к тому, что новая конъюнкция `х`z будет иметь дополнительное значение 1 на наборе (0, 0, 0), но f(0, 0, 0) = 0, поэтому переменную у также удалять нельзя.

в) Аналогично удаление`z приводит к тому, что новая конъюнкция будет иметь значение 1 на наборе (0, 1, 1). Поскольку f (0, 1, 1) = 0, то эту переменную нельзя удалять из набора.

Из а), б), в) следует, что элементарный набор N₁= (x, y,`z)является простым набором. Аналогичная проверка элементарных наборов N<sub>2</sub>= (x,` y,`z ) и N<sub>3</sub>= (x,`y, z) показывает, что у них можно удалить третью переменную. При этом конъюнкции, соответствующие новым наборам N^¢₂= N^¢₃= (x,`y),примут дополнительные единичные значения на тех наборах ((1,0,1) и (1,0,0)), где функция равна 1. Отсюда следует, что элементарные наборы N<sub>2</sub>=(x,` y,`z) и N<sub>3</sub>= (x,`y, z) не являются простыми наборами в СДНФ функции f.

Очевидно, что у любой минимальной нормальной формы внутренние функции должны содержать только простые наборы переменных. Поскольку обратное условие не является достаточным, то вводится понятие сокращенных нормальных форм.

Определение. Сокращенной дизъюнктивной, (шефферовой, конъюнктивной, веббовой) нормальной формой СкДНФ (СкШНФ, СкКНФ, СкВНФ) функции f(`хⁿ ) называют соответствующую нормальную форму, у которой во всех внутренних функциях j подставлены только простые наборы переменных.

Смысл сокращенных форм в том, что у них уже нельзя удалить переменные во внутренних функциях без нарушения правильности представления исходной функции.

Определение. Тупиковой дизъюнктивной, (шефферовой, конъюнктивной, веббовой) нормальной формой ТДНФ (ТШНФ, ТКНФ, ТВНФ) функции f(хⁿ) называют соответствующую нормальную форму, у которой нельзя удалить ни одну из внутренних функций j, входящих во внешнюю функцию F.

Так как внутренние функции j являются аргументами внешней функции F, то понятие тупиковой нормальной формы имеет смысл, сходный с сокращенной, с той лишь разницей, что минимальным является набор аргументов внешней функции, а не внутренних.

Очевидно, минимальная форма любой функции является одновременно и тупиковой. На этом свойстве основаны алгоритмы минимизации нормальных форм. Суть их заключается в том, что вначале строится множество всех тупиковых нормальных форм функции {Т}, а затем из них выбирается минимальная форма (зачастую их бывает несколько).

Метод покрытий

Метод включает в себя последовательное решение следующих задач.

I. Определение множества всех элементарных наборов функции {N}={N₁, ... , N_k} и совершенной нормальной формы.

II. Построение сокращенной нормальной формы и определение множества простых наборов {P}={P₁,...,P_s}, входящих в её внутренние функции.

III. Формирование матрицы А покрытий множества элементарных наборов {N}={N₁, ... , N_k} простыми наборами {P}={P₁, ...,P_s}.

IV. Построение решеточного выражения В и упрощение его, построение множества всех тупиковых нормальных форм {Т} и выбор из них минимальной формы (их может быть несколько).

Решение задачи I изложено в предыдущем пункте. Рассмотрим последовательно решение задач II — IV. Вначале II — построение сокращенной нормальной формы и определение множества простых наборов {P} = {P₁,...,P_s}.