Моделирование составных высказываний при помощи формул алгебры логики
Составные логические высказывания в повседневной жизни формулируют в словесном виде. Например, «если на улице идёт дождь, то надо взять с собой зонт либо остаться дома».
Для того, чтобы использовать аппарат логики для решения данных задач, необходимо вначале все словесные выражения в них представить в виде логических формул.
Последовательность такого перехода состоит из двух основных этапов.
1. Выделить в словесной постановке задачи все простые переменные высказывания, которые выражают только одну законченную мысль, не делимую на более мелкие смысловые фрагменты, и сопоставить им логические переменные. Например, в приведенном выше предложении такими простыми высказываниями являются следующие:
а) «на улице идёт дождь»;
б) «надо взять с собой зонт»;
в) «(надо) остаться дома».
Обозначим их, соответственно, латинскими буквами x,y,z и примем в качестве логических переменных.
2. Введенные на первом шаге логические переменные соединяют между собой логическими связками, правильно передающими смысл исходного словесного предложения.
При этом:
а) частицу «не» заменяют логической связкой Ø («отрицание») ;
б) союзы «и», «но», означающие одновременность выполняемых действий, заменяют логической связкой & («умножение»), имеющей такой же смысл в логике;
в) союзы «или», «либо», выражение «хотя бы один», означающие условие выполнение хотя бы одного из заданных действий, заменяют логической связкой Ú («логическое сложение»), имеющей такой же смысл в логике;
г) сочетания «если - то», «следовательно», означающие, что в паре высказываний из первого вытекает второе, заменяют логической связкой ® («импликация, логическое следование»), фраза ” А достаточно для В” передается прямой импликацией А® В, выражение ” А необходимо для В” передается обратной импликацией В® А ;
д) сочетания и слова «необходимо и достаточно», «равно», «все равно, что», «тождественно», «эквивалентно», означающие, что в паре высказываний из первого вытекает второе и одновременно из второго вытекает первое, заменяют логической связкой º («эквивалентность, логическое равенство») ;
е) словосочетание «либо - либо» имеет смысл исключающего “или” и означает, что из двух частей высказывания может быть истинным ровно одно, его заменяют логической связкой Å («сложение по модулю 2»).
Если то или иное логическое действие относится к группе простых высказываний, при необходимости в логической формуле надо использовать скобки.
В рассмотренном выше предложении из того факта, что на улице идёт дождь следует, что надо взять с собой зонт или остаться дома. В соответствии с перечисленными выше правилами, простые высказывания x,y,z, обозначающие эти действия, необходимо соединить между собой следующим образом: x® (y Ú z).
В сумме со смысловой расшифровкой переменных x,y,z, данная запись (логическая формула) полностью передает смысл исходного предложения. При этом формула поясняет логические связи понятий, использованных в нем.
Пример 1. Ввести булевские высказывания-переменные и составить при помощи логических связок формулу составного высказывания-пословицы: «всё равно, что в лоб, что по лбу».
Решение.
1. Выделим из словесного предложения простые переменные высказывания и обозначим их латинскими буквами: x = «в лоб»; y = «по лбу».
2. Соединяем между собой логическими связками введенные логические переменные. Сочетание «всё равно, что» заменяем связкой «эквивалентность»º .
В итоге получим следующий ответ: x = «в лоб»; y = «по лбу»; f(x,y) = (x º y).
Задачи
1. Определить, будут ли формулами алгебры логики следующие записи:
а)Ú(х,ØуÅ z, x®z);б) x¯(у|( y, zØ u);в) уºÅÚ( у®z,Øх, у);г) x&у ¯ (уºх, y,Ø z );д) xу Ú ¯ (у, z ).
Если выражение является формулой, указать правильный порядок выполнения действий. В неправильных записях указать ошибки.
2. Ввести булевские высказывания-переменные и составить при помощи элементарных булевых функций формулы составных высказываний:
а) «если в задаче ход решения неправильный или получен неверный ответ, то задача не засчитывается»,
б) «высказывания a и b одновременно верны или одновременно ложны тогда и только тогда, когда из высказывания a следует справедливость высказывания с»,
в) «рабочий процесс в аппарате может производиться только при условии загрузки емкости не менее чем на треть и температуры в ее рубашке не ниже 100 градусов и не выше 150 градусов».
3. Ввести булевские высказывания-переменные и построить таблицы истинности для следующих логических функций:
а) «если в комиссии из трех человек «за» голосует не менее двух человек, то принимается положительное решение»,
б) «если в комиссии из трех человек «за» голосует ровно два человека, то принимается положительное решение»,
в) аппарат оснащен четырьмя аварийными датчиками х, у, z, u.Автоматическое отключение главного двигателя происходит при срабатывании ровно одного из датчиков х и у,либо при совместном срабатывании z и u ,
г) машинный агрегат имеет датчики и концевые выключатели, обозначенные х, у, z, u. Пуск двигателя происходит при условии срабатывания датчиков х,у и отключенном u либо при срабатывании z , u и отключенных х, у.
4. Построить таблицы истинности функций, заданных следующими формулами:
а) х у ® у z; б) (х Ú у) Å ( х® у); в) (х¯`у х) ® х у; г) х (`х½у ) Å y; д) х ® ( у ® z ); е) х Å y ®`х y ; ж) ( х º у ) ® (`у®`х); з) (`у®`х ) ® (х® у).
5. Найти существенные и фиктивные переменные функций:
а)(хÅу)®`xz;б) х Ú (` у z Å x);в) ху Ú ху; г)(х® (у ® z))® ((x ® у)® (х® z)) ;д) (10100101); е) (00110011);ж) (10011010),з)(0101).
6. Привести собственный пример функции трех переменных, у которой две переменных являются фиктивными.
7. Доказать, что существует ровно две функции, у которых фиктивными являются все переменные.
8. Доказать, что при любом n существует ровно 4 n-местных пороговых функции, равных обобщенным функциям &(`хn),Ú (`х n), ¯(`х n), | (`х n).
9. Доказать, что число всех различных n-местных булевых функций равно 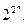
10. Доказать, что число всех различных n – местных булевых функций, у которых хотя бы одна переменная является фиктивной, равно 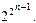
Дата добавления: 2020-10-14; просмотров: 655;











