Задание функции при помощи вектора истинности
Пример 2. Рассмотрим для примера функцию трех переменных f(х, у, z), имеющую следующую таблицу истинности:
| х | у | z | f |
При лексикографическом порядке расположения векторов значений переменных`хn они могут быть опущены и функция полностью будет задана своим вектором значений истинности f = (10110110).
Матричный способ
Заключается в том, что множество переменных`хn разбивается на две части`уm и`z n–m таким образом, что все возможные значения истинности вектора ` у m откладываются по строкам матрицы, а все возможные значения истинности вектора`z n - m ― по столбцам. Значения истинности функции f на каждом наборе `a n =(a1, ..., am,am+1,...,an)помещаются в клетки, образованные пересечением строки (a1, ..., am)и столбца(am+1,...,an).
В рассмотренном выше Примере 2 в случае разбиения переменных (х, у, z)на подмножества (х)и (у, z)матрица принимает вид:
| у , z | |||||
| х | |||||
Существенной особенностью матричного способа задания является то, что полные наборы переменных`хn, соответствующие соседним (как по вертикали, так и по горизонтали) клеткам, различаются по одной координате.
Задание с помощью полного бинарного дерева
Для описания n-местной функции f (`х n) используется свойство бинарного дерева высоты n, заключающееся в том, что каждой висячей вершине в нем взаимно однозначно соответствует некоторый набор значений вектора`хn. Соответственно, этой висячей вершине можно приписать такое же значение истинности, которое имеет на данном наборе функция f. В качестве примера (рис.1.3) приведем задание с помощью бинарного дерева рассмотренной выше трехместной функции f = (10110110).
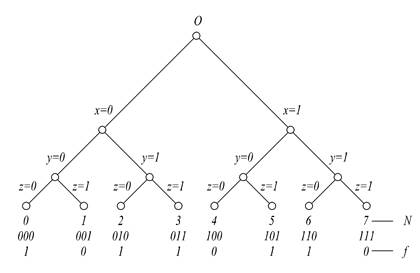
Рис.1.3
Первый ряд цифр, приписанных висячим вершинам дерева, обозначает лексикографический номер набора, второй ― сам набор, а третий ― значение функции на нем.
Задание с помощью n - мерного единичного куба В n
Поскольку вершины В n также можно взаимно однозначно отобразить на множество всех наборов`хn, то n-местную функцию f(хn) можно задать, приписывая ее значения истинности соответствующим вершинам куба В n. На рис.1.4 показано задание функции f =(10110110)на кубе В3. Значения истинности приписаны вершинам куба.
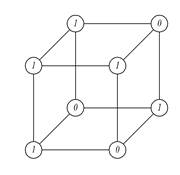
Рис.1.4
Определение. Алгеброй логики называют множество булевых констант и переменных вместе с введенными на них логическими связками.
Формульное задание
Функции алгебры логики могут быть заданы в виде аналитических выражений.
Определение. Пусть Х ―алфавит переменных и констант, используемых в алгебре логики, F ―множество обозначений всех элементарных функций и их обобщений при числах переменных, превышающих 2.
Формулой над Х,F (формулой алгебры логики) назовём все записи вида:
а) х, где хÎ X;
б) ØF1, F1&F2,F1ÚF2 , F1®F2, F1º F2, F1ÅF2, F1¯F2 , F1ïF2, где F1, F2 ― формулы над Х, F;
в) h(F1, … ,Fn ), где n > 2, F1,…, Fn ― формулы над Х, F, h ―обозначение обобщенной пороговой функции из F .
Как следует из определения, для двухместных элементарных функций используется инфиксная форма записи, при которой функциональный символ помещают между аргументами, для отрицания и обобщенных функций используют префиксную форму записи, при которой функциональный символ ставят перед списком аргументов.
Пример 3.
1. Выражения х&Ø(у®z); |(x, y, z Ú u) являются формулами алгебры логики, поскольку удовлетворяют данному выше определению.
2. Выражение ®х &(у | z)не является формулой алгебры логики, поскольку неправильно применена операция ®.
Определение. Функцией, реализуемой формулой F, называется функция, получаемая при подстановке значений переменных в F . Обозначим ее f(F).
Пример 4. Рассмотрим формулу F = ху Å(х®z). Для того, чтобы построить таблицу истинности реализуемой функции, необходимо последовательно с учетом силы логических связок выполнить логическое умножение ху, затем импликацию (х®z), после чего сложить полученные значения истинности по модулю 2. Результат выполнения действий показан в таблице:
| x | y | z | xy | х® z | F |
Формульное представление функций позволяет априори оценивать многие свойства функций. Переход от формульного задания к таблице истинности всегда может быть выполнен путем последовательных подстановок значений истинности в элементарные функции, входящие в формулу. Обратный переход неоднозначен, поскольку одна и та же функция может быть представлена различными формулами. Он требует отдельного рассмотрения.
Дата добавления: 2020-10-14; просмотров: 674;











