Описание эксперимента С. Дэшмана.

На страницах книги « Научные основы вакуумной техники» , ( изд. «Мир», 1964 г., стр. 584 ) С. Дэшман изложил свой эксперимент с электровакуумным диодом. На странице 584 приведены данные эксперимента в виде графика. В книге график построен на рисунке 9.14. В ходе эксперимента получено семейство кельвин-амперных характеристик, при различных напряжениях на аноде электровакуумного диода.

Рис.2.1. Текст из книги « Научные основы вакуумной техники».

С. Дэшман так описал свой эксперимент: « Вольфрамовая нить диаметром 0,25 мм расположена по оси цилиндра диаметром 2,54 см и длинной 7,62 см. Зависимость максимального тока от температуры выражается экспоненциальной кривой. Горизонтальные части кривых соответствуют току, ограниченному пространственным зарядом при различных Ua (напряжениях на аноде)» Эксперимент поставлен при весьма низких давлениях (порядка 1/ 1000 мтор или ниже).

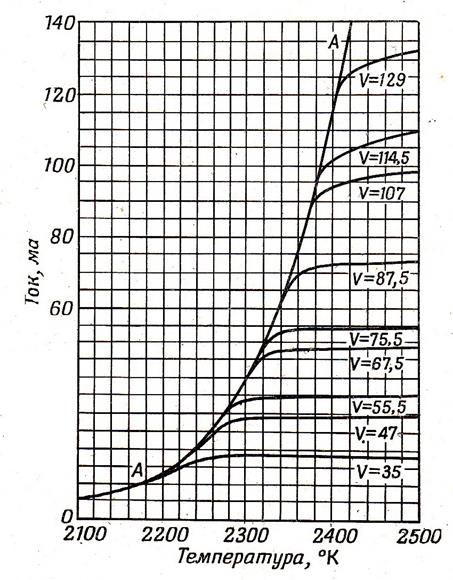
Рис.2.2. Рисунок на странице 584 из книги « Научные основы вакуумной техники».

Эксперимент С. Дэшмана показывает 2 процесса, влияющие на анодный ток электровакуумного диода. Первый процесс – электрический. Второй процесс – тепловой. С. Дэшман отметил в данном параграфе книги, что процессы ограничивают друг друга.

В дальнейшем мы обнаружим, что в электронных приборах всегда присутствует два процесса – электрический и тепловой. Это относиться и к полупроводниковым приборам. Электронное управление возможно в тех случаях, когда электрический ток сопровождается 2-мя процессами – электрическим и тепловым. Для получения явления электронного управления, выбор исследователей падает на вакуумные и полупроводниковые приборы, по причине соизмеримости в них тепловых и электрических процессов.

Экспериментальные данные из графика были переведены в таблицу, после чего экспериментальные данные были построены в виде графика на рисунке 2.3.

Рис. 2.3. Эксперимент С. Дэшмана. Кельвин-Амперные характеристики.

2.1.2. Математическая обработка результатов эксперимента С. Дэшмана. Кривая А-А′ как тепловой процесс.

Обратим внимание на экспоненциальную часть всех кривых. Обозначим эту кривую как А-А′. Кривая А-А′ соответствует кельвин-амперной характеристике при Ua более 150 Вольт, то есть когда отсутствует ограничение тока объёмным пространственным зарядом (ОПЗ) .

Считается, что ток ограничивается эмиссионной способностью катода, которая зависит от температуры. Величину этого предельного тока – тока насыщения - для каждой температуры и показывает кривая А-А′ . Обозначим кривую А-А′ как функцию

Ia = F₀₁(T)

При Ua > 150 В

где Ia – ток анода,

T – температура катода,

Ua – напряжение на аноде.

Кривая А-А′ из эксперимента С. Дэшмана построена при помощи точек на рисунке 2.4.

Рис 2.4. Кривая А-А′ из эксперимента С. Дэшмана.

Построим математическую модель функции: Ia = F₀₁(T). Для этого построим её график в полулогарифмическом масштабе на рисунке 2.5.

Рис. 2.5. Кривая А-А′ ( или функция F₀₁ ) из эксперимента С. Дэшмана, построенная в полулогарифмическом масштабе.

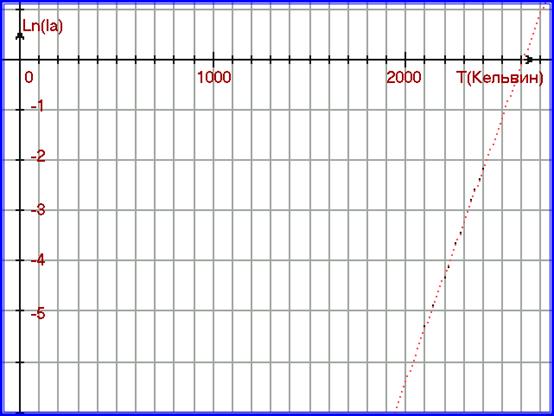
Рис. 2.6. Кривая А-А′ ( или функция F₀₁ ) из эксперимента С. Дэшмана, построенная в полулогарифмическом масштабе. Поверх неё построена математическая модель функции F₀₁ : Ln ( Ia ) = 1.047∙10^-2 ∙ T - 27.325 .

Кривая А-А′ (или функция F₀₁ ) в полулогарифмическом масштабе моделируется прямой линией по уравнению:

Ln( Ia ) = 1,047∙10^-2 ∙ T - 27,325

где Ia – ток анода в Амперах, T - температура катода в Кельвинах.

На рисунке 2.6. приведём математическую модель, построенную поверх экспериментальных данных – кривой А-А′. Графики выполнены в полулогарифмическом масштабе.

2.1.3. Математическая обработка результатов эксперимента С. Дэшмана. Кривая B-B′ как электрический процесс.

Кроме кривой А-А′ (см. рис. 2.3. ), на графике экспериментальных данных имеются также горизонтальные участки, которыми оканчиваются кельвин-амперные характеристики. Они зависят только от напряжения на аноде. По горизонтальным участкам получим функцию:

Ia = F₀₂ (Ua)

Построим график этой функции в виде кривой В-В′ на рисунке 2.7.

Рис. 2.7. Кривая В-В′ ( или функция F₀₂ ) из эксперимента С. Дэшмана.

Для того, чтобы построить модель для кривой В-В′, на рисунке 2.3. пронаблюдаем за горизонтальными участками кривых. Горизонтальные участки возникают при не очень высоких напряжениях и выражают собой закон ограничения тока объёмным пространственным зарядом – «закон 3/2». Для получения модели кривой В-В′ построим её в полном логарифмическом масштабе на рисунке 2.8.

На рисунке 6 экспериментальные данные кривой В-В′ располагаются в виде прямой с угловым коэффициентом 3/2. Отсюда находим математическую модель кривой В-В′ .

Ia = 9,215∙10^-5 ∙ Ua ^3/2

где Ia – ток анода в Амперах, Ua – напряжение на аноде в Вольтах.

На рисунке 2.9. построим математическую модель кривой В-В′ для полного логарифмического масштаба. В этом масштабе модель выражается уравнением:

Ln(Ia) = (3/2) ∙ Ln(Ua) - 9,292 .

Рис. 2.8. Кривая В-В′ ( или функция F₀₂ ) из эксперимента С. Дэшмана, построенная в полном логарифмическом масштабе.

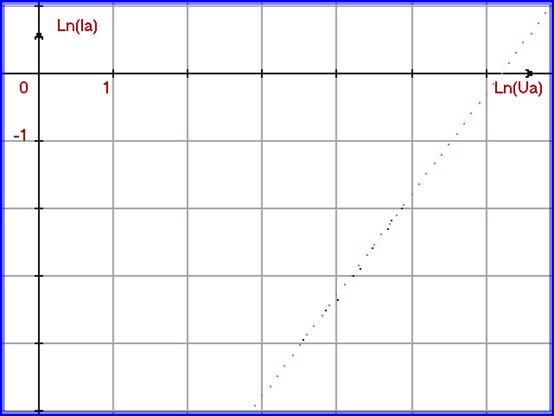
Рис. 2.9. Математическая модель кривой В-В′ , построенная в полном логарифмическом масштабе, поверх экспериментальных данных.