ЛАБОРАТОРНАЯ РАБОТА 3

СОРТИРОВКИ ЧИСЛОВЫХ МАССИВОВ.

РЕКУРСИВНЫЕ ФУНКЦИИ

Задание

Отсортировать по возрастанию числовой массив обменами, выбором, вставками, пузырьком и быстрой сортировкой. Получить зависимости временных затрат от размера массива. Временные затраты оценивать количеством сравнений и количеством обменов элементов массива. Сортировку выполнять на месте исходного массива.

СОРТИРОВКА ОБМЕНАМИ

Выполняется за n-1 проходов, где n – размер массива. В первом проходе первый элемент массива (с индексом 0) сравнивается с остальными элементами массива (с индексами 1…n-1) и, если предшествующий элемент больше последующего, они меняются местами. В последнем проходе сравниваются предпоследний и последний элементы массива. Следовательно, в каждом проходе количество сравнений фиксировано. Общее количество сравнений за сортировку равно n(n-1)/2.

Количество обменов зависит от состояния исходного массива. Если массив уже отсортирован, то обменов не будет. Это наилучший случай с точки зрения затрат машинного времени. Наихудший случай – при пересортировке массива, когда исходный массив отсортирован по убыванию. В этом случае каждое сравнение сопровождается обменом и, следовательно, количество обменов за сортировку равно n(n-1)/2.

СОРТИРОВКА ВЫБОРОМ

Эта сортировка требует также n-1 проходов. В первом проходе сравнениями первого элемента с остальными находят минимальный элемент и обменом помещают его на место первого элемента. В последнем проходе сравниваются предпоследний и последний элементы массива. Следовательно, в каждом проходе количество сравнений фиксировано. Общее количество сравнений за сортировку равно n(n-1)/2.

Число обменов всегда один на проход, следовательно, сортировка требует n-1 обменов. Наилучшего и наихудшего случаев не существует.

СОРТИРОВКА ВСТАВКАМИ

Выполняется за n-1 проходов. В первом проходе второй элемент массива (с индексом 1) сравнивается с первым элементом массива и, если второй оказывается меньше первого, первый сдвигается на место второго, а второй вставляется на место первого. В последнем проходе последний элемент массива сравнивается с предшествующими, начиная с предпоследнего, и вставляется между элементами, предыдущий из которых меньше, а последующий – больше последнего элемента. Среднее количество сравнений за сортировку - n(n-1)/4. Наилучший случай соответствует уже отсортированному массиву, когда количество сравнений равно n-1. Наихудший случай имеет место при пересортировке массива, при этом количество сравнений равно n(n-1)/2.

Обменов при сортировке вставками нет.

СОРТИРОВКА ПУЗЫРЬКОМ

В отличие от сортировки обменами, здесь сравниваются только соседние элементы и, если они стоят неправильно, меняются местами. В первом проходе сравниваются с соседним справа элементы с первого до предпоследнего. При этом сохраняется индекс первого из участвующих в последнем обмене элементов, что исключает избыточные просмотры массива. В следующем проходе просматривается часть массива с первого элемента по элемент с сохраненным индексом. Наилучший случай – массив уже отсортирован и нужен всего один проход с n-1 сравнениями. Наихудший случай – при пересортировке, когда потребуется n-1 проход с n(n-1)/2 сравнениями и n(n-1)/2 обменами.

БЫСТРАЯ СОРТИРОВКА

Быстрая сортировка содержит две фазы: сканирования и рекурсивную. На фазе сканирования в исходном массиве находят центральный по индексу элемент и массив разбивается на два подмассива – нижний и верхний. В нижний помещают элементы, меньшие или равные центральному, а в верхний – большие. Для этого нижний подмассив сканируют в направлении увеличения, а верхний – в направлении уменьшения индекса. Элементы, оказавшиеся не в своих подмассивах, меняются местами. Затем переходят к рекурсивной фазе, где описанным выше способом обрабатывают получаемые подмассивы, пока в них не окажется по одному элементу.

Наилучший случай соответствует отсортированному массиву с четным количеством элементов, когда число сравнений равно 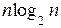. При пересортировке число сравнений практически такое же.

В наихудшем случае центральный элемент все время попадает в одноэлементный подмассив, а все остальные элементы остаются во втором подмассиве. Это происходит тогда, когда центральным всегда оказывается наименьший элемент. Здесь общее число сравнений равно n(n+1)/2-1. Однако этот случай маловероятен на практике.

РЕКУРСИВНЫЕ ФУНКЦИИ

В программировании рекурсия – вызов функции из этой же функции (простая рекурсия) или через другие функции (сложная рекурсия). Количество вложенных вызовов рекурсивной функции называют глубиной рекурсии. Рекурсивные функции реализуют рекурсивные алгоритмы.

Из вышеизложенного следует, что алгоритмы сортировок по существу являются рекурсивными алгоритмами, и поэтому сортировки естественно кодировать рекурсивными функциями. Однако большая глубина рекурсии приводит к переполнению стека, что является основным недостатком рекурсивных алгоритмов. Поэтому рекурсивные функции годятся для сортировок небольших по размеру массивов. Поскольку на практике обычно требуется сортировать данные больших объемов, то переходят к использованию итерационных алгоритмов, реализуемых циклами.

Приведем рекурсивные функции для указанных выше сортировок по возрастанию массива a длиной n. В приводимых функциях: swap() – вызов функции обмена, obm и sr – количество обменов и сравнений соответственно.

СОРТИРОВКА ОБМЕНАМИ

void SwapSort(int i, int j)

{ if(i==n-1) return;

if(j<n) {

if(a[i]>a[j]) {swap(a[i],a[j]); obm++;}

sr++; SwapSort(i,j+1);

}

else SwapSort(i+1,i+2);

}

Вызов функции - SwapSort(0, 1).

СОРТИРОВКА ВЫБОРОМ

void SelectSort(int i, int j, int min)

{ if(i==n-1) return;

if(j<n) {

if(a[min]>a[j]) min=j;

sr++; SelectSort(i, j+1, min);

}

else {

swap(a[i],a[j]); obm++;

SelectSort(i+1, i+2, i+1);

}

}

Вызов функции - SelectSort(0, 1, 0).

СОРТИРОВКА ВСТАВКАМИ

void InsertSort(int i, int j, int z)

{ if(i==n) return;

if(j>0&&z<a[j-1]) {

a[j]=a[j-1]; sr++;

InsertSort(i, j-1, z);

}

else {

a[j]=z; sr++;

InsertSort(i+1, i+1, a[i+1]);

}

}

Вызов функции - InsertSort(1, 1, a[1]).

СОРТИРОВКА ПУЗЫРЬКОМ

void BubbleSort(int i, int j, int last)

{ if(i<=0) return;

if(j<i) {

if(a[j]>a[j+1]) {swap(a[i],a[j]); obm++; last=j;}

sr++; BubbleSort (i,j+1,last);

}

else BubbleSort (last,0,0);

}

Вызов функции - BubbleSort (n-1,0,0).

БЫСТРАЯ СОРТИРОВКА

void QuickSort(int l, int h)

{ int su,sd,m,p;

if(h-l<=0) return;

else if(h-l==1) {

if(a[h]<a[l]) { swap(a[l],a[h]); obm++; }

sr++;

return;

}

m=(l+h)/2; p=a[m]; swap(a[m],a[l]); obm++; su=l+1;sd=h;

do {

while(su<=sd && a[su]<=p) {su++; sr++;}

while(p<a[sd]) {sd++; sr++;}

if(su<sd) {swap(a[su],a[sd]); obm++; }

} while(su<sd);

a[l]=a[sd]; a[sd]=p; obm++;

if(l<sd-1) QuickSort(l,sd-1);

if(sd+1<h) QuickSort(sd+1,h);

}

Вызов функции - QuickSort(0,n-1);

Данные для формирования массивов и размещения результатов сортировки массивов, а также функции сортировок инкапсулированы в классе. Объявление класса:

class array {

public:

array(int); //конструктор 1 (с параметром)

array(array&); //конструктор 2 (копии)

void swap(int&, int&); //обмен элементов массива

void SwapSort(int, int); //обменная сортировка

void SelectSort(int, int, int); //сортировка выбором

void InsertSort(int, int, int); //сортировка вставками

void BubleSort(int, int, int); //сортировка пузырьком

void QuickSort(int, int); //быстрая сортировка

void out_mass_a()const; //вывод массива

int get_sr() const; //получение количества сравнений

int get_obm() const; //получение количества обменов

~array() {delete [] a;} //деструктор

private:

int* a; //указатель для формирования массива

int n; //размер массива

int sr; //количество сравнений

int obm; //количество обменов

};