Арифметические основы цифровых устройств.

Импульсные и цифровые устройства

Импульсные и цифровые устройства относятся к категории устройств дискретной электроники, работа которых основана на использовании свойств электронных ключей. Электронные ключи используются для коммутации электрических сигналов, и могут находиться всего в двух состояниях: «открыто» или «закрыто». Электронные ключи выполняют на полупроводниковых диодах, биполярных и полевых транзисторах.

К импульсным устройствам относятся различные управляемые и неуправляемые генераторы, формирователи и преобразователи импульсов, которые широко используются в составе цифровых устройств с памятью.

К цифровым устройствам относятся узлы комбинационного типа (без памяти), способные выполнять арифметические и логические операции, кодирование и декодирование сигналов, и др. К цифровым устройствам также относятся цифровые автоматы (с памятью), способные запоминать свои состояния (триггеры), коды чисел (регистры), выполнять счет импульсов (счетчики импульсов) и др.

Арифметические основы цифровых устройств.

В цифровых устройствах в основном применяются только позиционные системы счисления (ПСС). Позиционной называется такая система счисления, в которой значение цифры зависит от ее позиции (разряда) в записи числа. Примером является десятичная ПСС. Переходя от младшего разряда к более старшему проходим позиции (разряды) единиц, десятков, сотен и т.д.

Принципы построения ПСС являются общими для всех ПСС.

Пусть р – основание ПСС. Последовательность символов {0;1;..р-1} – цифры ПСС. Тогда любое число А в р-ичной ПСС может быть представлено в виде последовательности цифр этой ПСС:

.

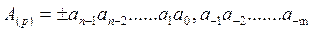При этом а_i принадлежит множеству {0;1;..р-1}. Последовательность цифр слева от запятой – это целая часть числа. Последовательность цифр справа от запятой – это дробная часть числа.

Оценить значение этого числа мы можем только в десятичной ПСС, а значит его следует перевести в десятичную ПСС. Это делается с помощью полинома вида:

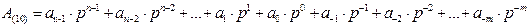. (14.1)

В цифровых устройствах практическое применение находят двоичная ПСС, десятичная ПСС и шестнадцатиричная ПСС. Соответствие цифр перечисленных ПСС приведено в табл. 14.1.

Из табл. 14.1 видно, что каждая шестнадцатиричная цифра представляется четырехразрядным двоичным числом. Расположение разрядов во всех ПСС одинаково: справа младшие разряды, а слева – старшие.

Таблица 14.1.

Двоичная ПСС получила самое широкое применение в цифровых устройствах потому, что две ее цифры «0» и «1» отождествляются с состояниями электронного ключа «открыто» и «закрыто». А это позволило создать устройства, выполняющие арифметические и логические операции, а также запоминающие устройства.

Десятичная ПСС используется только для ввода и вывода информации в форме, удобной для человека.

Шестнадцатиричная ПСС используется только для упакованной формы представления двоичных чисел при вводе и выводе информации.

Правило перевода чисел из двоичной ПСС в шестнадцатиричную. Двигаясь от запятой вправо и влево разбивают число на группы по четыре цифры, дополняя неполные группы в начале и в конце числа нулями. Затем каждую группу из четырех цифр заменяют одной шестнадцатиричной цифрой по таблице 14.1. Пример:

00110001,10111000₍₂₎=31,В8₍₁₆₎

Правило перевода чисел из шестнадцатиричной ПСС в двоичную. Каждая шестнадцатиричная цифра заменяется четырехразрядным двоичным числом по таблице 14.1. Пример:

4F,CА₍₁₆₎=0100 1111,1100 1010₍₂₎

Правило перевода чисел из десятичной ПСС в двоичную (шестнадцатиричную). Перевод целой и дробной части числа выполняется раздельно по разным алгоритмам.

Для перевода целой части числа, ее делят на основание р=2, ниже записывают целую часть частного, а напротив – остаток. На следующем шаге делению подвергают полученную целую часть частного. Эта последовательность действий повторяется многократно до получения целой части частного, равной нулю. Число в двоичной ПСС запишется в виде остатков от деления, начиная с последнего частного, представляющего собой старшую цифру числа. Пример:

35/2 ¦ 1

17/2 ¦ 1

8/2 ¦ 0

4/2 ¦ 0

2/2 ¦ 0

1/2 ¦ 1

0 Результат перевода: 35₍₁₀₎=100011₍₂₎

Для перевода дробной части числа, ее умножают на основание р=2, ниже записывают целую часть произведения, отделяя ее от новой дробной части. На следующем шаге умножению подвергают новую дробную часть произведения. Эта последовательность действий повторяется многократно до получения нулевой дробной части, или до получения необходимого количества разрядов после запятой. Число в двоичной ПСС запишется в виде целых частей произведений начиная с первого произведения (сверху вниз). Пример:

0,125ּ2

0¦25ּ2

0¦5ּ2

1¦0 Результат перевода: 0,125₍₁₀₎=0,001₍₂₎

Перевод чисел из любых ПСС в десятичную выполняется с помощью полинома (14.1).

Арифметические операции в двоичной ПСС выполняются по тем же правилам, что и в десятичной.

Контрольные вопросы

1. Принцип построения и форма представления чисел в позиционных системах счисления (ПСС)?

2. Как выполняется перевод чисел из любой р-ичной ПСС в десятичную?

3. Понятие двоичной и шестнадцатиричной ПСС, их использование?

4. Перевод чисел из двоичной системы счисления в десятичную, переведите число 1101,101₍₂₎ в десятичную ПСС?

5. Перевод чисел из шестнадцатиричной системы счисления в десятичную, переведите число 7АС,8D₍₁₆₎ в десятичную ПСС??

6. Перевод чисел из двоичной системы счисления в шестнадцатиричную, переведите число 11011001,101₍₂₎ в шестнадцатиричную ПСС?

7. Перевод чисел из шестнадцатиричной системы счисления в двоичную, переведите число 1FD,6A8₍₂₎ в двоичную ПСС?

8. Выполните суммирование двоичных чисел 1101₍₂₎ и 1010₍₂₎?

9. Выполните вычитание двоичных чисел 1101₍₂₎ и 1010₍₂₎?

10. Выполните умножение двоичных чисел 1101₍₂₎ и 1010₍₂₎?