Скалярный потенциал магнитного поля

Для совокупности точек, где 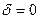, , 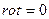магнитное поле можно рассматривать как потенциальное, т.е. каждая точка этого поля имеет свой магнитный потенциал -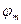

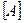
Для таких областей можно записать

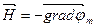
Так как

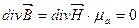
При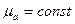

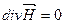
Получим

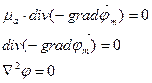
Получили уравнение Лапласа для скалярного магнитного потенциала:

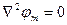
Оно справедливо только для областей, не занятых током.

Разность скалярных магнитных потенциалов между точками 1 и 2 называют падением магнитного напряжения между точками 1 и 2.

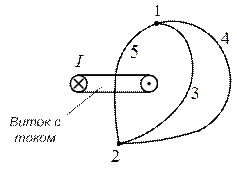
Падение магнитного напряжения между точками 1 и 2 по пути 1-3-2 равно падению магнитного напряжения между точками 1 и 2 по пути 1-4-2 в том случае, когда эти пути (1-3-2 и 1-4-2) образуют замкнутый контур, ток внутри которого равен нулю. Если же эти пути образуют замкнутый контур, ток внутри которого не равен нулю (например контур 1-3-2-5-1), то падения магнитного напряжения по пути 1-5-2 и по пути 1-3-2 не будут равны и будут отличаться на значение тока, охваченного контуром. Т.е. по закону полного тока можно записать:

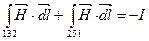
Для того, чтобы разность магнитных потенциалов между двумя точками не зависела от пути, наложим запрет на прохождение пути через контур с током. При прохождении контура с током магнитный потенциал будет меняться скачком на значение тока в контуре.

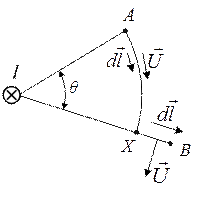
Пример 1:Определить разность магнитных потенциалов между точками А и В.

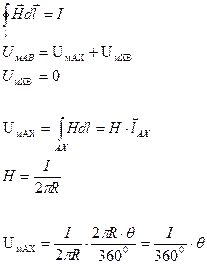
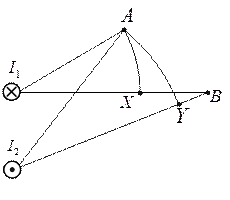
Пример 2: Определить разность магнитных потенциалов в случае действия нескольких токов.

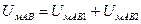
Граничные условия

Первое граничное условие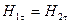

На границе раздела двух сред, различных в магнитном отношении ( 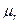различна), равны тангенциальные составляющие векторов напряжённости магнитного поля.

Доказательство:

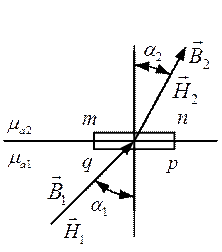
Составим циркуляцию вектора напряженности по плоскому контуру mnpq 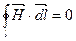. Пренебрежём циркуляцией вектора напряжённости магнитного поля на участках mq и np, так как контур плоский. Обозначим сторону mn и равную ей сторону qp за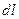

Так как

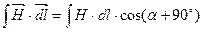
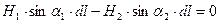
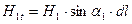
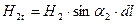
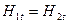
Это условие не выполняется, если на поверхности раздела двух сред протекает поверхностный ток.

Поверхностный ток-ток, протекающий по бесконечно тонкому листу проводника, помещенному на границу раздела двух сред.

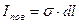
где 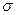- линейная плотность тока

Поверхностный ток направлен перпендикулярно плоскости, его знак берется по правилу правого винта.

Тогда циркуляция вектора напряженности магнитного поля по плоскому контуру равна поверхностному току, который оказался внутри

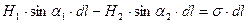
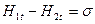
Второе граничное условие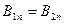

На границе раздела двух сред, различных в магнитном отношении ( 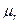различна), равны нормальные составляющие векторов магнитной индукции.

Доказательство:

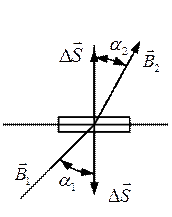
На границе раздела выделим небольшой плоский параллелепипед и подсчитаем потоки вектора магнитной индукции через верхнею и нижнюю грани. Принцип непрерывности магнитного потока: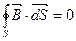

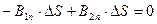
Следовательно:

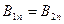
Из граничных условий вытекает соотношение:

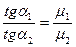
Оно даёт связь между углом падения и углом преломления.