Основные уравнения и законы
Закон полного тока в интегральной форме
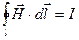
Циркуляция вектора напряженности по замкнутому контуру равна алгебраической сумме токов, пронизывающих контур (полный ток). Под полным током понимают весь ток, пронизывающий контур интегрирования (ток проводимости и ток смещения).
Этот закон позволяет рассчитать контур в случае прямых длинных проводников.
Пример:
Рассчитать напряженность поля в точке А в поле уединенного прямого провода с током I.
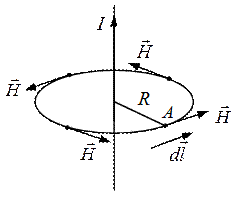
Проведем через точку А окружность радиусом R в плоскости перпендикулярной оси провода. В силу симметрии напряженность поля во всех точках окружности одна и та же, а направление напряженности совпадает с касательной к окружности.
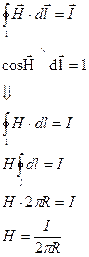
Закон полного тока в дифференциальной форме
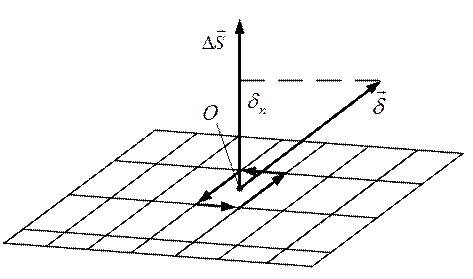
Выделим небольшой контур и составим для него циркуляцию вектора напряженности. Циркуляция вектора напряженности вдоль малого контура равна току, пронизывающему этот контур. Так как контур мал, то в пределах этого контура плотность тока одинакова.
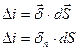
где 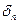 проекция вектора плотности тока на нормаль к площади.
проекция вектора плотности тока на нормаль к площади.
За положительное направление нормали к площади принимают направление движения острия правого винта, головка которого вращается в направлении, принятом за положительное при обходе контура и составлении циркуляции
Тогда: 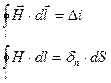
Разделим обе части равенства на элементарную площадь и устремим элементарную площадку к нулю
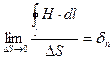
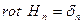
Если площадку ориентировать в пространстве так, что направление нормали совпадет с направлением вектора плотности тока 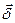 , то вместо проекций двух векторов можно записать равенство самих векторов.
, то вместо проекций двух векторов можно записать равенство самих векторов.
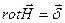 - дифференциальная форма закона полного тока.
- дифференциальная форма закона полного тока.
Ротор – это функция, характеризующее поле в рассматриваемой точке в отношении способности к образованию вихрей.
Магнитное поле всегда вихревое.
В том случае, когда 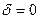 ,
, 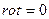 , магнитное поле можно считать условно потенциальным, т.е. каждая точка поля обладает каким–то потенциалом, неизменным во времени.
, магнитное поле можно считать условно потенциальным, т.е. каждая точка поля обладает каким–то потенциалом, неизменным во времени.
Раскрытие ротора в декартовой системе координат
Равенство векторов 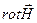 и
и 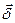 означает, что равны их проекции на оси x,y,z
означает, что равны их проекции на оси x,y,z
Проекция ротора на направление оси z
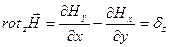
Проекция ротора на направление оси x
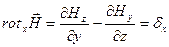
Проекция ротора на направление оси y
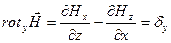
Таким образом,
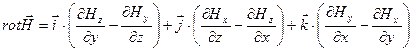
Выражение проекций ротора в цилиндрической и сферической системах координат
В цилиндрической системе координат:
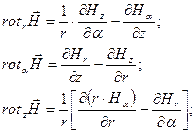
В сферической системе координат:
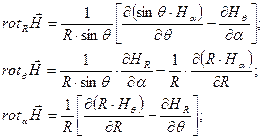
Дата добавления: 2020-10-14; просмотров: 672;











