Деформированное состояние тела

Выделим в теле прямоугольный параллепипед. После нагружения он трансформируется в косоугольный, то есть появляются линейные и угловые деформации. Деформированное состояние характеризуется тензором деформаций. Этот тензор будет симметричным, так как g_ху = g_ух (угловые деформации одного и того же прямого угла).

Сравним основные квадратичные формы для нормального напряжения и линейной деформации:

s_n = s_x×l² + s_y×m² +s_z×n² + 2t_yx×m×l + 2t_zx×n×l + 2t_zy×n×m

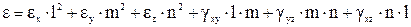
Как видно, формулы полностью аналогичны. Коэффициенты при направляющих косинусах являются составляющими тензора деформаций:

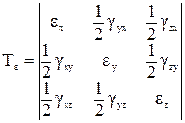(74)

Также существуют инварианты деформированного состояния, которые определяются аналогично инвариантам напряженного состояния:

q₁ = e_х + e_у + e_z,

q₂ = e_х×e_у + e_у×e_z + e_z×e_х - 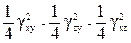, (75)

q₃ = Т_e.

Для определения величины главных деформаций существует основное характеристическое уравнение деформированного состояния:

e³ - q₁×e² + q₂×e - q₃ = 0

Корни данного уравнения нумеруются в порядке убывания: e₁ ³ e₂ ³ e₃. Главные деформации - это линейные деформации в направлении, перпендикулярном главным площадкам деформации, а главными площадками деформации являются такие, в которых угловые деформации равны нулю. Главные площадки расположены по трем взаимно перпендикулярным осям, которые называются главными осями деформированного состояния.