Постановка задачі цілочислового лінійного програмування
Існує досить широкий клас задач математичного програмування, в оптимальному розв’язку яких змінні приймають дробові значення, що з економічної точки зору не має змісту, наприклад, коли говориться про випуск певної продукції (комп’ютерів, меблів, станків і т.д.). Тому це призвело до нового класу задач - задач цілочислового програмування. В загальному випадку така задача має вигляд:
Знайти максимум (мінімум) функції
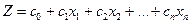 (6.1)
(6.1)
за умов
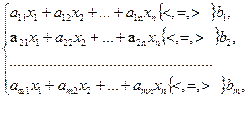 (6.2)
(6.2)
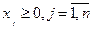
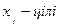 (6.3)
(6.3)
До задач цього класу можна віднести задачу про використання сировини, транспортну задачу, задачу раціонального розкрою матеріалів, а інший клас задач цілочислового програмування містить задачі оптимізації, в яких змінні набувають лише двох цілих значень - 0або 1 (бульові змінні). Прикладом такої задачі є задача про комівояжера, її зміст полягає в тому, що комівояжеру потрібно відвідати кожне з п міст, починаючи і закінчуючи свій маршрут в одному й тому ж місті і не заїжджаючи двічі в одне місто. Якщо між містами і та j немає прямого маршруту, то вважають, 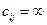 (на практиці беруть достатньо велике число). Крім цього, можливо, що
(на практиці беруть достатньо велике число). Крім цього, можливо, що 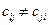 . Задача полягає у знаходженні найкоротшого шляху комівояжера. Математична модель задачі має вигляд:
. Задача полягає у знаходженні найкоротшого шляху комівояжера. Математична модель задачі має вигляд:
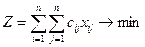
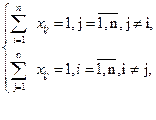 (6.4)
(6.4)
де 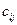 - відстань між містами і та j;
- відстань між містами і та j; 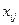 - бульові змінні:
- бульові змінні:
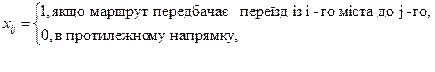
Обмеження, задані першою формулою в системі (6.4), - це умова щодо одноразового в’їзду в кожне місто, а другою формулою - щодо одноразового виїзду з кожного міста.
Розглянемо ще один приклад задачі з бульовими змінними. Інвестиційна компанія може вкласти кошти в декілька підприємств. Ефективність кожного проекту оцінена згідно з тим, що його реалізація можлива за певних умов. Кожному проекту відповідає невідома, яка рівна 1 чи 0 залежно від того, вкладає чи не вкладає інвестиційна компанія кошти в підприємство.
В деяких реальних задачах ставиться умова цілочислових значень не до всіх змінних, а до однієї чи декількох. Такі задачі називають частково цілочисловими.
Дата добавления: 2016-07-22; просмотров: 1871;











